8.4. Сложение вращательных движений нмс вокруг двух параллельных осей

Пусть НМС вращается с угловой скоростью вокруг оси O₁z, которая, в свою очередь, вместе с НМС вращается с угловой скоростью вокруг неподвижной оси О₂, параллельной оси O₁z (рис. 81 – 82).

Вращательное движение НМС вокруг оси O₁z – относительное движение НМС, а вращательное движение оси O₁z вместе с НМС вокруг неподвижной оси О₂ – переносное движение.

Все точки НМС, как в относительном, так и в переносном движениях, остаются в плоскостях, перпендикулярных осям O₁z и О₂, т. е. в параллельных между собой плоскостях. Поэтому сложное движение НМС является плоскопараллельным движением НМС и абсолютное движение НМС в каждый момент времени может быть сведено к рассмотрению мгновенного вращательного движения плоского сечения НМС с угловой скоростью вокруг мгновенного центра скоростей (вращения).

Сечение НМС плоскостью, перпендикулярной осям O₁z и О₂, изображено на рис. 81 – 82. Точки B и D – точки пересечения этих осей с плоскостью сечения.

При определении положения мгновенного центра скоростей (вращения) и угловой скорости возможны три случая.

8.4.1. Вращательные движения нмс направлены в одну сторону

Точка D вращается только относительно оси О₂, двигаясь со скоростью V_D=₂BD, направленной в плоскости сечения перпендикулярно BD (рис. 81).

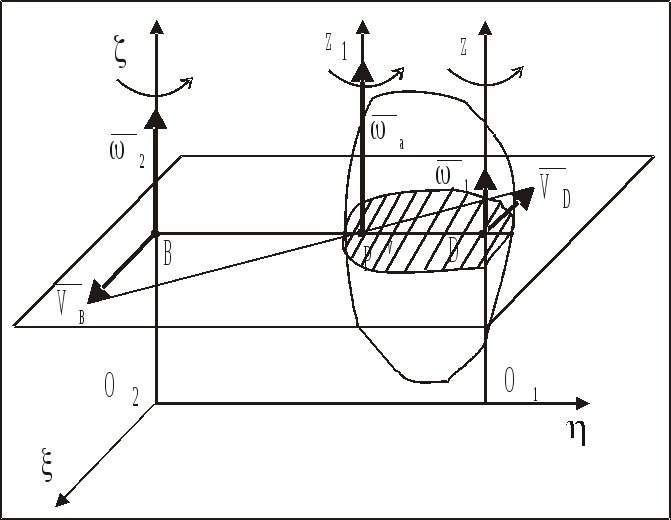
Рис. 81

Точка В вращается только относительно оси О₁z, двигаясь со скоростью V_В=₁BD, направленной в плоскости сечения перпендикулярно BD в противоположную сторону (рис. 81).

Используя третий способ нахождения мгновенного центра скоростей (рис. 33), определим его положение – точку Р^v (рис. 81).

Тогда на основании формулы (4.5) для угловой скорости абсолютного движения НМС относительно оси Р^vz₁ можно записать:

(8.5) или . (8.6)

Подставив выражения V_В=₁DB и V_D=₂DB в (8.6), получим пропорцию, которая определяет положение мгновенного центра скоростей – :

. (8.7)

Для выражения угловой скорости абсолютного движения НМС через угловые скоростиииз (8.5), используя свойства пропорции, можно получить:

а с учетом формул для скоростей V_В=₁BD и V_D=₂BD определим угловую скорость абсолютного движения НМС

т. е.

. (8.8)

Если НМС вращается одновременно относительно двух параллельных осей в одну и ту же сторону с угловыми скоростями и, то абсолютное движение НМСбудет мгновенным вращательным с абсолютной угловой скоростью вокруг мгновенной оси вращения, параллельной данным осям. Положение этой оси определяется пропорцией (8.7). Абсолютная угловая скорость направлена в ту же сторону, что и угловые скорости относительного и переносного движения.

8.4.2. Вращательные движения нмс направлены в разные стороны и 12

Точка D вращается только относительно оси О₂, двигаясь со скоростью V_D=₂BD, направленной в плоскости сечения перпендикулярно ВD (рис. 82).

Точка В вращается только относительно оси О₁z, двигаясь со скоростью V_В=₁BD, направленной в плоскости сечения перпендикулярно BD в ту же сторону, что и (рис. 82).

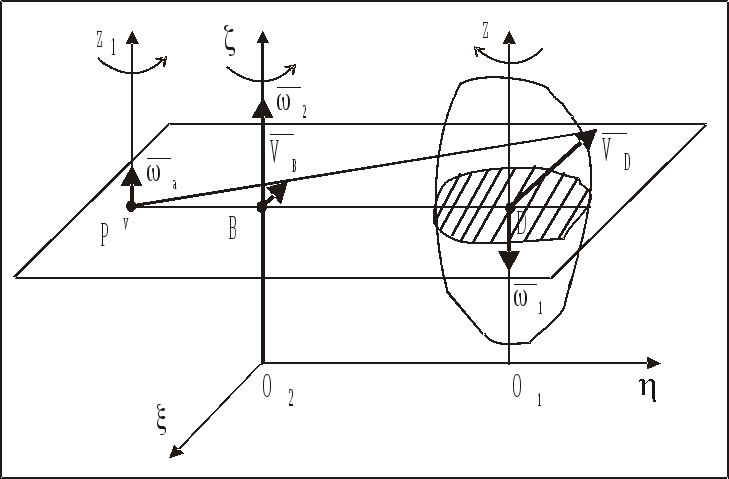
Рис. 82

Используя третий способ нахождения мгновенного центра скоростей (рис. 33) и для определенности полагая, что ₂>₁, определим его положение — точку P^v (рис. 82).

Проделав операции аналогичные проделанным в случае, рассмотренным в п. 8.4.1, получим:

(8.9)

и

(8.10)

(при выводе формулы (8.9) также используется свойство пропорции только для разности числителей и знаменателей).

Если НМС вращается одновременно относительно двух параллельных осей в разные стороны с различными по модулю угловыми скоростями и, то абсолютное движение НМС будет мгновенным вращательным с абсолютной угловой скоростью вокруг мгновенной оси, параллельной данным. Положение оси определяется пропорцией (8.9). Абсолютная угловая скоростьнаправлена в сторону большей угловой скорости.