Решение.

1. Находим коэффициенты пористости по ступеням давлений по формуле:

=0,740-(1+0,740)*0,155/25=0,730

=0,740-(1+0,740)*0,240/25=0,723

=0,740-(1+0,740)*0,325/25=0,717

=0,740-(1+0,740)*0,405/25=0,712

=0,740-(1+0,740)*0,510/25=0,704

=0,740-(1+0,740)*0,610/25=0,698

2. Найдем коэффициент сжимаемости грунта по формуле:

1. ρ=0,100÷0,200:

2. 2) ρ=0,100÷0,300:

3. ρ=0,200÷0,300:

3. Найдем коэффициент относительной сжимаемости грунта по формуле:

1. ρ=0,100÷0,200:

2. ρ=0,100÷0,300:

3. ρ=0,200÷0,300:

4. Найдем компрессионный модуль деформации по формуле:

1. ρ=0,100÷0,200: МПа

2. ρ=0,100÷0,300: МПа

3. ρ=0,200÷0,300: МПа

5. Найдем модуль общей деформации по формуле:

Значение коэффициента для суглинка найдем интерполяцией по среднему значению коэффициента пористости:

1. ρ=0,100÷0,200: МПа

2. ρ=0,100÷0,300: 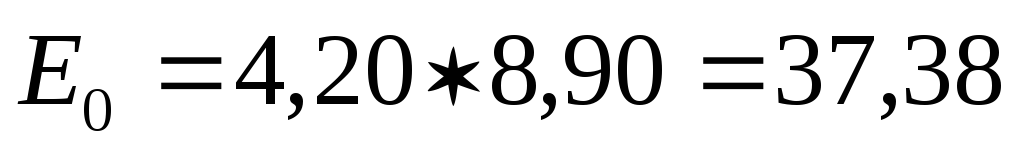МПа

3. ρ=0,200÷0,300: 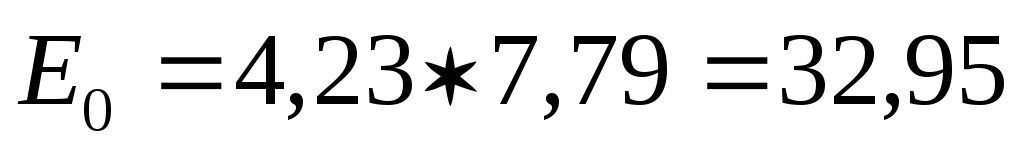МПа

Задача 3. Определение модуля общей деформации по результатам полевых испытаний штампом.

Модуль общей деформации Е0 определяется по формуле:

где v – коэффициент Пуансона, принимаемый равным 0,3;

k – коэффициент, принимаемый 0,79 для жесткого круглого штампа;

d – диаметр штампа определяем исходя из площади подошвы штампа:

∆p – приращение давления на штамп, равное

∆S – приращение осадки штампа, равное

Определяем модуль общей деформации Е0:

Задача 4. Определение вертикальных сжимающих напряжений σz в точке от действия сосредоточенных сил Р1, Р2, Р3.

где P1 P2 P3 – приложенные сосредоточенные силы;

r – расстояние по горизонтали от оси Z, проходящей через точку приложения сосредоточенной силы;

К – коэффициент определяемый из таблицы в зависимости от соответствующих отношений ri / z.

Определяем вертикальные сжимающие напряжения σz:

Задача 5. Определить вертикальные сжимающие напряжения σz и построить эпюру распределения σz.

Для вычисления вертикального сжимающего напряжения используем формулу:

где q – распределенная нагрузка;

Кz – коэффициент, значения которого приведены в таблице в зависимости от относительных координат z/b и y/b:

z – расстояние (глубина) от точки М1 до точки М10 (от 0 м до 9 м);

b – расстояние от вертикальной оси Z до оси определения напряжения;

y – длина распределенной нагрузки.

В точке М1

В точке М2

В точке М3

В точке М4

В точке М5

В точке М6

В точке М7

В точке М8

В точке М9

В точке М10

Задача 6. Прямоугольный фундамент имеет длину l и ширину b. Интенсивность равномерно распределенной нагрузки от фундамента на основание q. Методом угловых точек определить вертикальные сжимающие напряжения σz в точке М с координатами X, Y, Z.

Напряжение в точке М (вне прямоугольника давления) складывается из суммы напряжений от действия нагрузки по прямоугольникам Mhbe и Mecf, взятых со знаком "+", и напряжений от действия нагрузки по прямоугольникам Mhag и Mgdf, взятых со знаком "-".

где К1С, К2С, К3С, К4С – угловые коэффициенты, определяемые по формуле:

Задача 7. Насыпь создает трапецеидальную нагрузку с интенсивностью q=100 кПа на основание. Определить вертикальные сжимающие напряжения σz в точке М с координатами X,Y.

1. При нагрузке действующей слева:

По монограмме определяем

2. При нагрузке действующей справа:

По монограмме определяем

3. Таким образом:

Задача 8. Построить эпюры распределения напряжения от собственного веса грунта для трех расчетных схем.

Дано:

№ ИГЭ	Наименование грунта	Удельный вес грунта , кН/м³	Удельный вес частиц грунта , кН/м³	Коэффициент пористости е
1	Супесь аллювиальная	20,3	26,6	0,51
2	Песок мелкий	18,6	26,7	0,72
3	Глина аллювиальная твердая(водоупор)	19,1	27	0,74

Построить Эпюры распределения напряжений от собственного веса грунта для 3-х расчетных схем.

Решение.

І схема

№ИГЭ-1:

№ИГЭ-2:

№ИГЭ-3:

Эпюра распределения напряжений к І схеме

І І схема

№ИГЭ-1:

№ИГЭ-2:

-выше У.Г.В. :

-нижеУ.Г.В:

; ; кН/м³

№ИГЭ-3:

Эпюра распределения напряжений к ІІ схеме

ІІІ схема

№ИГЭ-1:

№ИГЭ-2:

-выше У.Г.В. :

-ниже У.Г.В. :

№ИГЭ-3:

Эпюра распределения напряжений к ІІІ схеме

Задача 9. Определить первую и вторую критическую нагрузку на основание от заглубленного ленточного фундамента шириной b, глубиной заложения h.

Исходные данные:

b=4м; h=3м; γ=18,6кН/м3; с=11кПа;

Решение.

1. Найдем начальную критическую(безопасную) нагрузку на грунт:

(При ; )

3. Найдем вторую критическую (предельную) нагрузку на грунт:

Для краевых точек (при у=0 и у=b)

пред (1)

пред (2)

По табл. для вертикальной нагрузки (δ=0) при . Найдем значения коэффициентов Ny, Nq, Nc интерполяцией.

Подставляя эти значения в формулы (1) и (2), будем иметь :

пред

пред

Тогда пред ≈0,9 МПа.

Задача 10. Определить максимальную высоту вертикального откоса h для глинистого грунта.

Дано:

γ =19,5 кН/м³; с=25кПа;

φ=11град.

Определить максимальную высоту вертикального откоса h для глинистого грунта.

Решение.

Определяем максимальную высоту вертикального откоса h, где устойчивость вертикального откоса в грунтах обладает трением и сцеплением ().Тогда получаем формулу:

3,11м

Задача 11. Определить величину активного ЕА и пассивного ЕП давления грунта на подпорную стенку.

Исходные данные:

Н=8,9м

h=3м

кН/м³

с=12кПа

Определить величину активного и пассивного давления грунта на подпорную стенку.

Решение.

Давление связности:

Активное давление грунта:

Пассивное давление грунта:

Задача 12. Определить осадку ленточного фундамента на естественном основании

Методом послойного суммирования.

Исходные данные:

N=735кН

B=2,4м

H=3м

кН/м³

E=9МПа

Определить осадку ленточного фундамента на естественном основании методом послойного суммирования.