1.4. Теоретические основы уравнивания геодезических измерений

При создании съемочного обоснования может быть выполнено достаточное и избыточное количество измеренных элементов в геодезических построениях. При недостаточном количестве измерений нет возможности проконтролировать их правильность. Но при выполнении избыточных измерений увеличивается количество затраченного времени и уменьшается производительность труда. Поэтому после рекогносцировки, при составлении схемы (проекта) планово-высотного обоснования, необходимо планировать выполнение избыточных измерений. При этом следует стремиться к такой схеме измерений, при которой было бы минимальное количество избыточных измерений, но достаточное их количество для осуществления контроля правильности этих измерений (рис. 6). Например, для вычисления всех элементов треугольника достаточно измерить одну его сторону и два примыкающих к этой стороне угла (рис. 6а). Но проконтролировать правильность полученных результатов после вычисления всех элементов треугольника невозможно. Тогда как, выполнив избыточное измерение только одного третьего угла треугольника (см. рис. 6б) и сопоставив сумму этих углов со значением теоретической суммы равной 180, появляется уверенность в правильности этих измерений. При этом нет необходимости выполнять большое количество избыточных измерений. Это не только уменьшает производительность труда, но и определяет лишние (чрезмерно избыточные) условия, которые порой трудно учесть при определении поправок в измеренные значения. Например, нет необходимости измерять все три угла и все три стороны в треугольнике. Выявленную погрешность измерений (невязку) можно распределить в измеренные параметры (вычислить поправки и уравнять), тем самым увеличить достоверность конечных результатов.

2

а) б)

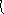
Рис. 6. Достаточное (а) и избыточное (б) количество измерений в треугольнике для вычисления его элементов.

Кроме того, абсолютное значение погрешности (невязки) сопоставляется с допускаемой погрешностью. Допустимые или ожидаемые погрешности зависят от выбранного метода измерений и точности используемых приборов. Поэтому при проектировании сети планово-высотного обоснования следует помнить, что количество измерений должно быть необходимым и достаточным для определения правильности выполненных измерений и реализации математического метода определения поправок в измеренные параметры, а метод измерений и применяемые приборы соответствовать необходимой точности измерений.

Как известно, погрешности измерений бывают грубые, систематические и случайные. Грубые промахи в измерениях и систематические погрешности выявляются и исключаются из результатов измерений путем или повторных измерений (грубые промахи) или специальными методами (поправка за компарирование мерного прибора и др.). Грубые и систематические погрешности в данном случае нами не рассматриваются.

Случайные погрешности могут быть исключены из результатов измерений только путем уравнивания геодезических измерений. Процесс сопоставления функций измеренных параметров с их теоретическими значениями, вычисление случайных погрешностей (невязок), сравнение их с допустимыми и отбраковка недоброкачественных измерений, а также определение поправок в измеренные параметры по условию вычисления их вероятнейших значений, называется уравниванием геодезических измерений.

Для уравнивания используются методы математической обработки геодезических измерений. Необходимость уравнивания диктуется условием, при невыполнении которого может происходить одностороннее накопление погрешностей в конечных результатах измерений (координатах и отметках точек). Эти погрешности, в конечном итоге, могут превысить необходимую точность составляемого плана или точность определения точек проектируемого объекта на местности.

В зависимости от класса точности измерений при реализации математических методов различают:

• строгое уравнивание, когда вычисление поправок в измеренные параметры определяют путем составления и решения систем математических уравнений;

• нестрогое уравнивание, когда поправки в измеренные параметры вычисляют путем приближенного определения их вероятнейших значений.

Суть строгого и не строгого уравнивания поясним на примере уравнивания углов геодезического четырехугольника (рис. 7).

Пусть в этой сети измерены восемь углов β₁,β₂,β₃,β₄,β₅,β₆ β₇,β₈. Каждый угол измерен одним и тем же теодолитом с неизвестными погрешностямиδβ₁,δβ₂,δβ₃,δβ₄,δβ₅,δβ₆ δβ₇,δβ₈. Для уравнивания необходимо в каждый угол ввести поправки v₁,v₂, v₃, v₄, v₅, v₆, v₇, v₈, которые с наибольшей вероятностью должны быть равны абсолютной величине погрешностей измерений и противоположны им по знаку.

Для строгого уравнивания геодезического четырехугольника составляют восемь уравнений с неизвестными поправками v₁,v₂,v₃,v₄,v₅,v₆, v₇, v₈

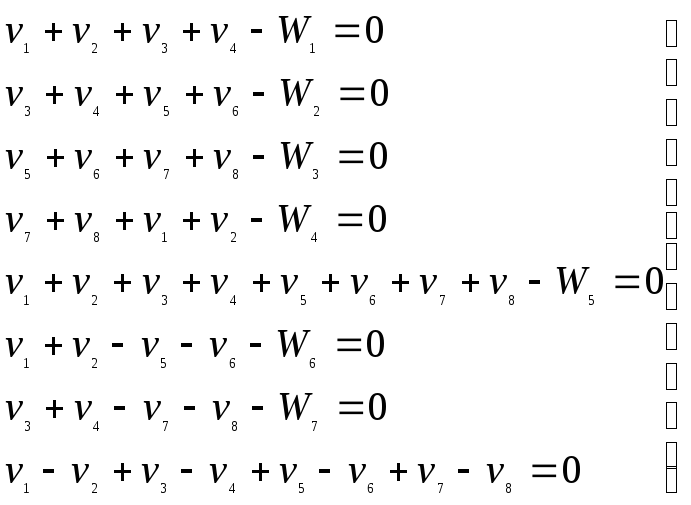(14)

гдеW₁,W₂,W₃,W₄,W₅ – невязки соответственно в треугольниках и четырехугольнике.

W₆,W₇– невязки по суммам углов в смежных треугольниках.

Первые пять уравнений системы (14) определяются из следующих геометрических условий.

W₁=β₁+β₂+ β₃+β₄ -180°;

W₂=β₃+β₄ + β₅+ β₆- 180°;

W₃= β₅+ β₆+β₇+ β₈ - 180°; (15)

W₄= β₇+ β₈+β₁+ β₂ - 180°;

W₅=β₁+β₂ + β₃ + β₄ + β₅ + β₆+β₇+ β₈ − 360°.

Следующие два уравнения в системе (14) определяются из условий

W₆= β₁ + β₂ – β₅ – β₆

W₇= β₃ + β₄ – β₇ – β₈

Последнее уравнение в системе (14) получено из условия

β₉+β₁₀ +β₁₁+β₁₂ = 360

где β₉ = 180° – (β₁+β₂), так какv₉ = 0, то v₁– v₂= 0

β₁₀ = 180° – (β₃+β₄), так какv₁₀ = 0, то v₃– v₄= 0

β₁₁ = 180° – (β₅+β₆), так какv₁₁ = 0, то v₅– v₆= 0

β₁₂ = 180° – (β₇+β₈), так какv₁₂ = 0, то v₇– v₈= 0

Математически строгое решение системы уравнений (14) приводит к искомому результату.

При не строгом уравнивании поправки определяются по тем же принципам, что и при строгом уравнивании. То есть, численные значения поправок равны их вероятнейшему значению из условия равноточности или неравноточности измеренных параметров. В любом случае удовлетворяются основные геометрические условия (15), по которым устанавливаются невязки.

3 β₃ + δβ₃

β₄ + δβ₄

4

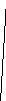
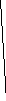
2

5

β₂+ δβ₂

β₅+ δβ₅

1

2

β₁₁

11

β₁₀ 10

5

9 β₉

12 β₁₂

β₁+ δβ₁

β₆+ δβ₆

3

4

1

6

5

β₇+δβ₇

8 β₈+ δβ₈

7

11

Рис. 7. Схема опорной сети (геодезический четырехугольник)

1.5. Теория способа наименьших квадратов

В качестве основного теоретически обоснованного способа уравнивания геодезических систем планового и высотного обоснования используется способ наименьших квадратов. Способ используется как для уравнивания сети обоснования при выполнении съемочных работ, так и для иных геодезических измерений.

Теоретическая суть способа заключается в следующем.

Допустим, что имеет место серия измеренных параметров, функции которых определяются следующей последовательностью чисел:

X₁,X₂,X₃, …,X_n.

Каждой функции в этой последовательности соответствуют погрешности:

∆₁, ∆₂, ∆₃, …, ∆_n,

которые подчиняются закону нормального распределения и имеют свою вероятность появления. Совокупность случайных погрешностей определяется в соответствии с теоремой умножения их вероятностей. В этом случае будем иметь:

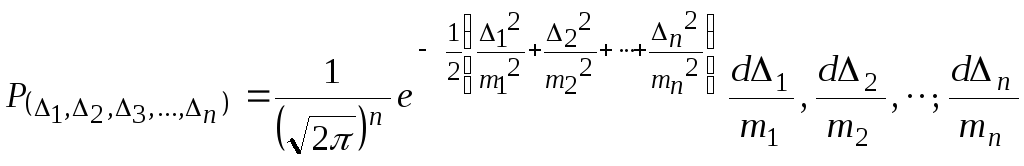, (16)

где n– количество измерений;

m– среднеквадратическая погрешность;

d∆i– дифференциал погрешности.

Анализ формулы (16) показывает, что максимальной вероятности появления совокупности распределений погрешностей в левой части уравнения, будет соответствовать наименьшее абсолютное значение показателя степени в правой части этого уравнения. То есть,

. (17)

Или, если для поправок V_iпоставить условие

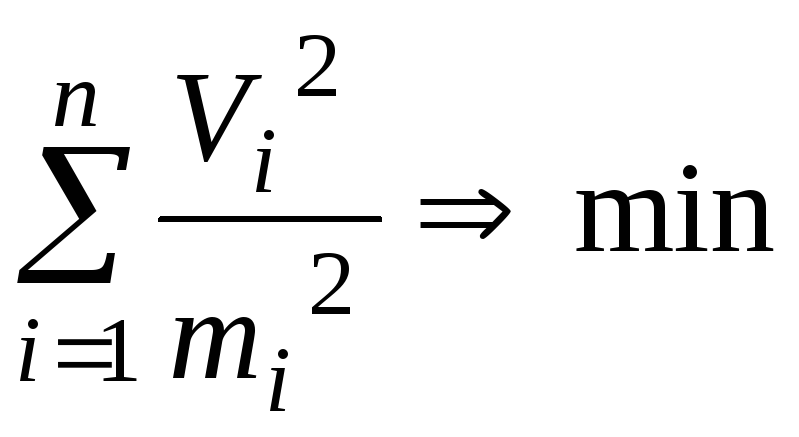, (18)

аналогичное требованию (17), то оно наилучшим образом приводит к соответствующим погрешностям измерений. Как известно весовой коэффициент измерений устанавливается формулой:

, (19)

где - произвольно выбранное число.