5 СТРУКТУРНЫЕ МОДЕЛИ СИСТЕМ

Различают статические и динамические структурные модели. Статические модели представляют собой функции вида:

,

(5.1)

где x и y – входные и выходные параметры системы, которые не зависят от времени, либо их значения рассматриваются как установившиеся. Функция f при этом может задаваться аналитически, графически или алгоритмически.

Динамические модели описываются линейными и нелинейными дифференциальными уравнениями, разностными уравнениями, уравнениями в частных производных, операторными уравнениями, передаточными функциями и т.д. Описанию систем с помощью динамических моделей и посвящена данная лекция.

5.1 Основные определения

Рассмотрим систему со входным сигналом u(t) и выходным сигналом y(t). Система называется стационарной, если значение выходного сигнала зависит только от значения входного сигнала и не зависит от времени. Система называется линейной, если её реакция на сумму двух входных сигналов равна сумме реакций на каждый сигнал. Система называется причинной, если значение выходного сигнала зависит только от предшествующих значений входного сигнала.

Линейная стационарная причинная система может быть полностью описана своей импульсной характеристикой (весовой функцией) :

.

(5.2)

Обычно на практике рассматриваются дискретные системы и сигналы. В этом случае:

.

(5.3)

В реальности на систему действует не только входной сигнал, но и различные внешние возмущения, которые также должны быть включены в модель:

,

(5.4)

где v(t) – возмущение. К возмущениям относится любой внешний сигнал, который мы не можем контролировать. Наиболее часто встречаются два источника возмущений: ошибки измерения входного или выходного сигнала и входы, неучтённые в модели. Обычно возмущение рассматривается как случайная величина и для его характеристики применяют функции распределения, функции плотности вероятности, ковариационные функции, а также значения среднего и дисперсии. Часто возмущение представляют как результат прохождения белого шума e(t) через линейную систему с импульсной характеристикой h(k):

.

(5.5)

Введём оператор сдвига вперёд q:

и оператор сдвига назад q^-1:

.

Тогда выражение (5.3) может быть переписано в виде:

.	(5.6)
Функция G(q) называется передаточной функцией системы.

Аналогично, для выражения (5.5) можно записать:

.

(5.7)

Тогда общее выражение для линейной системы с аддитивным возмущением может быть записано так:

.

(5.8)

Для реальных систем важно понятие устойчивости. При подаче на вход устойчивой системы ограниченного входного сигнала выходной сигнал будет также ограничен. Система с передаточной функцией G(q) и частотной характеристикой g(k) будет устойчива в том случае, если выполняется соотношение:

.

(5.9)

Для устойчивости системы необходимо, чтобы передаточная функция G(q) не имела полюсов (значений, при которых функция стремится к бесконечности) внутри круга единичного радиуса на комплексной плоскости.

5.2 Модели «чёрного ящика»

С помощью передаточных функций может быть построено несколько типов моделей. В простейшем случае функции G и H рассматриваются как рациональные функции, а коэффициенты полиномов в числителе и знаменателе этих функций становятся параметрами модели. Такие модели также называются моделями «чёрного ящика», так как с их помощью может быть лишь описана взаимосвязь между входами и выходами системы, но не внутренняя структура или законы функционирования.

Наиболее просто взаимодействие между входом и выходом может быть представлено в виде линейного разностного уравнения:

(5.10)

Так как белый шум e(t) вносит ошибка прямо в разностное уравнение, такую модель также называют моделью ошибки предсказания. Вектора параметров модели:

(5.11)

Введём обозначения

,

тогда

(5.12)

Модель (5.10) также называется ARX-моделью, при этом AR означает «autoregressive» (авторегрессионная), а X – дополнительный вход B(q)u(t) (в эконометрике этот вход называется экзогенно, то есть внешней, переменной). В случае, если n_a = 0, y(t) рассматривается как выход фильтра с конечной импульсной характеристикой (КИХ-фильтра). Такая модель широко применяется при решении задач цифровой обработки сигналов.

Оценка выходного сигнала модели (5.10) может быть вычислена так:

.

(5.13)

Введём обозначение для наблюдаемых значений входного и выходного сигналов:

.

(5.14)

Тогда (5.13) примет вид:

.

(5.15)

Такая модель в статистике называется линейной регрессией, а вектор φ(t) – вектором регрессии. Для определения вектора параметров модели могут быть применены простые, но мощные методы.

Основной недостаток модели (5.10) состоит в недостаточной гибкости описания возмущения. Можно сделать модель более гибкой, если описать ошибку модели как скользящее среднее белого шума. В результате получится модель:

(5.16)

Введя обозначение

(5.16)

получим

.

(5.17)

В вектор параметров модели теперь входят и коэффициенты с₁,…, с_n.. Такая модель называется ARMAX.

Наконец, ошибку модели (5.10) можно описать и с помощью авторегрессии. В результате получим модель

(5.18)

Такая модель, по аналогии с предыдущими, называется ARARX.

Предположим теперь, что взаимосвязь между входом и невозмущённым выходом может быть описана с помощью линейного разностного уравнения. Тогда можно записать

(5.19)

Введя обозначение

получим модель, называемую моделью выходной ошибки:

.

(5.20)

Наиболее общая форма модели чёрного ящика может быть записана в следующем виде:

.

(5.21)

Если система имеет задержку на k отсчётов, модель принимает вид:

.

(5.22)

5.3 Модели пространства состояний

В моделях пространства состояний зависимость между векторами входа, выхода и шума описывается дифференциальными или разностными уравнениями первого порядка с использованием дополнительного вектора состояний x(t).

Модели большинства физических систем проще строить для непрерывного времени в силу того, что физические законы сформулированы именно для случая непрерывного времени. Функционирование физической системы можно описать дифференциальным уравнением

.

(5.23)

Здесь F и M – матрицы с размерами, соответственно n×n и n×m для системы с n состояниями и m входами. θ – вектор параметров, которые обычно соответствуют неизвестным значениям физических коэффициентов, материальных констант и т.д. Моделирование выполняется в терминах переменных состояния x, имеющих физический смысл (положение, скорость и т.д.), а измеренные выходы зависят от состояний. Пусть η(t) – измерения, получаемые с помощью идеальных (не подверженных шумам и ошибкам измерения), датчиков:

.

(5.24)

Используем оператор дифференцировании p и перепишем уравнение (5.23):

.

(5.25)

Тогда η(t) и x(t) можно связать выражением:

(5.26)

Таким образом получена непрерывная модель с использованием передаточной функции, при этом модель имеет параметры, соответствующие физическим коэффициентам.

В реальности η(t) подвержен шумам и ошибкам измерений. Существует несколько способов учесть эти ошибки в модели. Рассмотрим простейший из них. Пусть измерения дискретизированы с интервалом T, возмущения в точках дискретизации равны v_T(kT), k = 1, 2, …, тогда измеренные значения выходного сигнала определяются выражением:

.

(5.27)

Теперь необходимо определить вид передаточной функции G_c в дискретном случае. Предположим, что входной сигнал постоянен на интервале дискретизации T:

.

(5.28)

Тогда дифференциальное уравнение может быть решено на интервале [kT; (k+1)T]:

,

(5.29)

где

(5.30)

Используя оператор сдвига вперёд q, выражение (5.29) можно переписать в виде:

,

(5.31)

или

,

(5.32)

Наконец, (5.27) может быть переписано так:

.

(5.33)

Без потери общности можно предположить, что T = 1 и переписать выражения (5.29) и (5.33) (H = C(θ):

(5.34)

или

(5.35)

Дальнейшее уточнение модели достигается добавлением модели шума v(t):

,

(5.36)

где e(t) – белый шум с дисперсией λ. При использовании моделей в пространстве состояний часто шум v(t) разделяют на шум измерений n(t) и шум процесса w(t)

(5.37)

Предполагается, что w(t) и n(t) – последовательности независимых случайных величин с нулевым средним и известной ковариационной функцией.
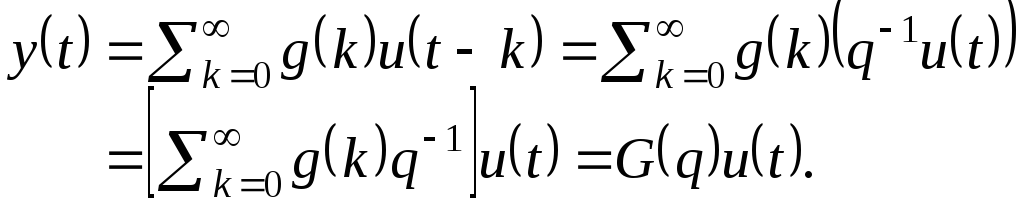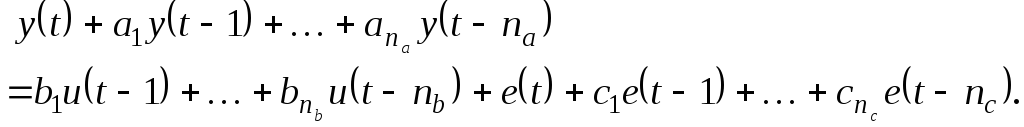
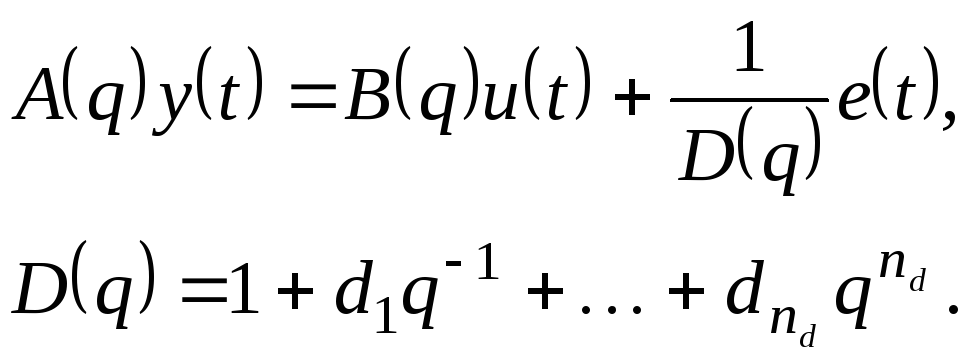
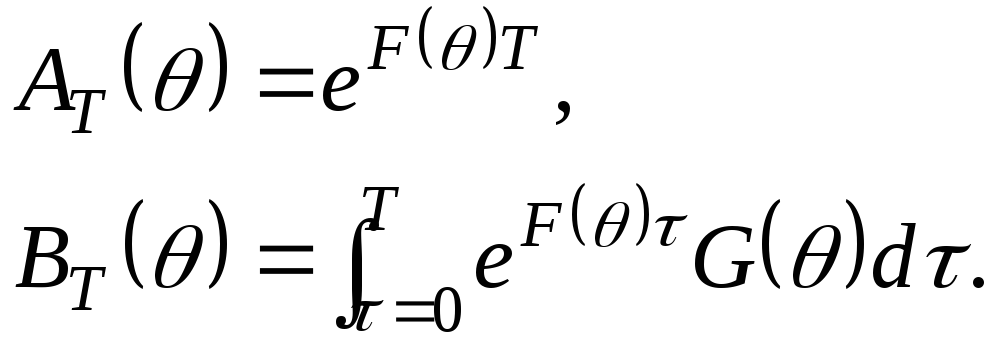
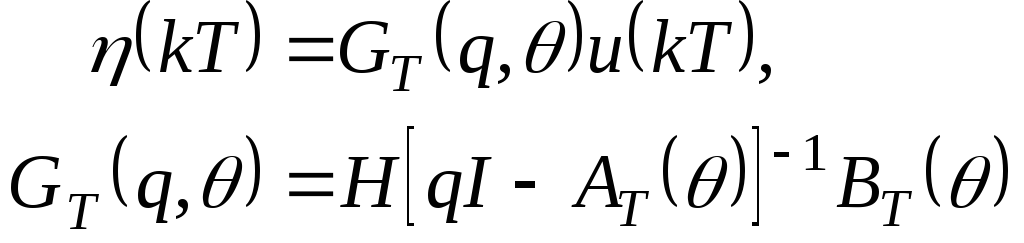