Лекция 15 - Транспортная задача

15 ТРАНСПОРТНАЯ ЗАДАЧА

Транспортные задачи представляют собой специальный класс задач линейного программирования. В этих задачах обычно описывается перемещение какого-либо товара из пунктов отправления (мест производства) в пункты назначения (склады, магазины). Основная цель состоит в определении объёма перевозок из пунктов отправления в пункты назначения с минимальной суммарной стоимостью перевозок. При этом должны учитываться ограничения, налагаемые на объем грузов в пункте назначения (ограничения предложения) и ограничения, учитывающие потребность в грузах в пунктах назначения (ограничения спроса). В транспортной задаче предполагается, что стоимость перевозки груза по какому-либо маршруту прямо пропорциональна объёму груза, перевозимого по этому маршруту.

Несмотря на то, что транспортная задача может быть решена как обыкновенная задача линейного программирования, её специфическая структура позволяет использовать для решения упрощённый алгоритм.

15.1 Определение транспортной модели

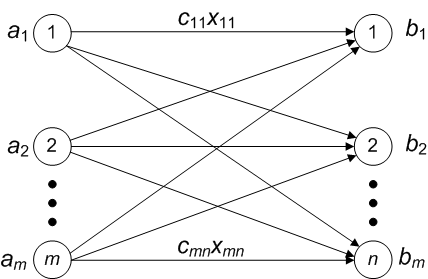
Графическое представление условий транспортной задачи приведено на рис. 15.1. На рисунке показано m пунктов отправления и n пунктов назначения, которые представляют собой узлы сети. Дуги, соединяющие узлы сети, соответствуют маршрутам, связывающим пункты отправления и пункты назначения. С каждой дугой (i, j) между пунктами i и j связывается два параметра: стоимость перевозки c_ij и объём перевозимых грузов x_ij. Объём груза в пункте i равен a_i, максимальное количество груза в пункте назначения j равно b_j. Задача состоит в определении неизвестных величин x_ij, минимизирующих суммарные транспортные расходы и удовлетворяющих ограничениям предложения (a_i) и спроса (b_j).

В рамках транспортной модели могут рассматриваться также задачи управления запасами и задачи распределения оборудования для выполнения различных работ.

Рис. 15.1. Представление транспортной задачи в виде сети.

Транспортная задача может быть представлена также и в табличном виде. При таком представлении каждая строка соответствует пункту отправления, каждый столбец – пункту назначения, число в ячейке на пересечении i-й строки и j-го столбца показывается стоимость перевозки, неизвестное значение в такой ячейке – объём перевозок. В последней ячейке каждой строки записано ограничение предложения, в последней ячейке каждого столбца - ограничение спроса.

Таблица 15.1

	1	2	…	n
1	c11 x11	c12 x12	…	c1n x1n	a1
2	c21 x21	c12 x12	…	c2n x2n	a2
…	…	…	…	…	…
m	cm1 xm1	cm2 xm2	…	cmn xmn	am
	b1	b2	…	bn

15.2 Решение транспортной задачи

Специальный алгоритм решения транспортной задач был специально разработан для быстрых ручных вычислений. В настоящее время большинство компьютерных программ использует для решения транспортной задачи симплекс-метод. Однако специальный алгоритм всё-таки представляет интерес, так как позволяет лучше понять особенности транспортной задачи.

Решение транспортной задачи рассмотрим на следующем примере. Некоторая транспортная компания занимается перевозкой зерна специальными зерновозами от трёх элеваторов к четырём мельницам. В таблице 15.2 показаны возможности элеваторов по поставке зерна (предложение) и потребность мельниц в зерне (спрос). Спрос и потребность измеряются в зерновозах. Кроме того, в таблице представлена стоимость c_ij перевозки зерна от элеваторов к мельницам в сотнях долларов.

Таблица 15.2

	1	2	3	4
1	10 x11	2 x12	20 x13	11 x14	15
2	12 x21	7 x12	9 x23	20 x24	25
3	4 x31	14 x32	16 x33	18 x34	10
	5	15	15	15

Последовательность этапов алгоритма решения транспортной задачи повторяет аналогичную последовательность этапов симплекс-метода:

1. определяется начальное базисное допустимое решение;

2. на основании условия оптимальности среди всех небазисных переменных выбираем переменную, вводимую в базис; если все небазисные переменные удовлетворяют условию оптимальности, вычисления заканчиваются, в противном случае переходят к третьему этапу;

3. с помощью условия допустимости определяют переменную, исключаемую из базиса; затем находят новое базисное решение и возвращаются ко второму этапу.

Для построения начального базисного решения транспортной задачи могут использоваться метод северо-западного угла, метод наименьшей стоимости и метод Фогеля. В общем случае метод Фогеля даёт наилучшее решение, а метод северо-западного угла – наихудшее. Однако метод северо-западного угла требует меньшего объёма вычислений.

Выполнение метода северо-западного угла начинается с ячейки x₁₁ (северо-западный угол). Метод включает следующие этапы:

1. переменной x₁₁ присваивается максимальное значение, допускаемое ограничениями на спрос и предложение;

2. вычёркивается строка или столбец с полностью реализованным предложением или с удовлетворённым спросом; если одновременно удовлетворяется и спрос, и предложение, то вычёркивается либо строка, либо столбец;

3. если не вычеркнута только одна строка или только один столбец, процесс останавливается; в противном случае переходят к ячейке справа (если вычеркнут столбец) или к ячейке слева (если вычеркнута строка), после чего возвращаются к первому этапу.

Рассмотрим применение метода к данным из примера. Максимальное значение x₁₁, удовлетворяющее ограничениям спроса и предложения, равно 5. Приписываем это значение x₁₁, вычёркиваем столбец 1 и переходим к ячейке x₁₂. Учитывая то, что предложение в строке один уже частично удовлетворено на предыдущем шаге, максимальное значение x₁₂ равно 10. Вычёркиваем первую строку и переходим к ячейке x₂₂. Продолжая действовать аналогично, получаем результат, приведённый в таблице 15.3.

Таблица 15.3

	1	2	3	4
1	10 5	2 10	20	11	15
2	12	7 5	9 15	20 5	25
3	4	14	16	18 10	10
	5	15	15	15

Базисное решение, полученное по методу северо-западного угла: x₁₁=5, x₁₂=10, x₂₂=5, x₂₃=15, x₂₄=5, x₃₄=10. Суммарная стоимость перевозок при таком решении рана 520.

Метод наименьшей стоимости находит лучшее начальное решение, чем метод северо-западного угла, поскольку выбирает переменные, которым соответствуют наименьшие стоимости. Сначала по всей таблице ищется ячейка с наименьшей стоимостью. Соответствующей переменной присваивается максимальное значение, допускаемое ограничениями спроса и предложения. После этого вычёркивается строка или столбец, соответствующая удовлетворённому значению предложения или спроса. Если одновременно удовлетворяются оба ограничения, вычёркивается либо столбец, либо строка. Затем просматриваются невычеркнутые ячейки, среди них ищется ячейка с минимальной стоимостью, после чего процесс повторяется заново. Процесс повторяется до тех пор, пока не останется лишь одна невычеркнутая строка или столбец.

Таблица 15.4

	1	2	3	4
1	10	2 15	20	11 0	15
2	12	7	9 15	20 10	25
3	4 5	14	16	18 5	10
	5	15	15	15

Вновь обратимся к нашему примеру. Минимальную стоимость имеет ячейка x₁₂. Максимальное значение, удовлетворяющее и спрос, и предложение равно 15. Приписываем переменной x₁₂ значение 15 и вычёркиваем второй столбец (могли бы вычеркнуть и первую строку). Следующее минимальное значение в невычеркнутой части – 4 (x₃₁). Переменной x₃₁ присваиваем значение 5, которое полностью удовлетворяет спрос. Вычёркиваем первый столбец. Следует отметить, что при присвоении переменной в ячейке значения мы должны соответствующим образом скорректировать значение неудовлетворённого спроса или предложения. Поэтому после последнего описанного шага значение предложения третьего элеватора станет равно 5.

Действуя аналогичным образом, получаем результат, приведённый в таблице 15.4. Переменным в невычеркнутом столбце необходимо присвоить значения, которые удовлетворяли бы оставшимся ограничениям. Такие значения также указаны в таблице. Полученное начальное базисное решение имеет вид: x₁₂=15, x₁₄=0, x₂₃=15, x₂₄=10, x₃₁=5, x₃₄=5. Соответствующее значение целевой функции: z = 475.

Метод Фогеля является вариацией метода наименьшей стоимости и в общем случае находит лучшее начальное решение. Метод Фогеля включает следующие шаги.

1. Для каждой строки или столбца, которым соответствует положительное значение предложения или спроса, вычисляется штраф путём вычитания наименьшей стоимости из следующей по величине в данной строке или столбце.

2. Выбирается строка или столбец с наибольшим штрафом. В выделенной строке или столбце выбирается переменная с наименшьшей стоимостью, и ей присваивается наибольшее значение, позволяемое ограничениями. В соответствии с присвоенным значением корректируется величина неудовлетворённого спроса и нереализованного предложения. Строка или столбец с удовлетворённым ограничением вычёркивается из таблицы. Если одновременно выполняются оба ограничения, то произвольно вычёркивается строка или столбец, причём оставшемуся ограничению присваивается нулевое значение.

3. Если не вычеркнута только одна строка или только один столбец с нулевым спросом или предложением, вычисления заканчиваются. Если не вычеркнута одна строка (столбец) с положительным предложением (спросом), в этой строке (столбце) методом наименьшей стоимости находятся базовые переменные и вычисления заканчиваются. Если всем невычеркнутым строкам и столбцам соответствуют нулевые объёмы предложения и спроса, методом наименьшей стоимости находятся нулевые базисные переменные, и вычисления заканчиваются. Во всех остальных случаях переходят к пункту 1.

Таблица 15.5

	1	2	3	4		Штраф
1	10	2	20	11	15	8
2	12	7	9	20	25	2
3	4 5	14	16	18	10	10
	5	15	15	15
Штраф	6	5	7	7

Используем метод Фогеля для определения начального решения в примере с элеваторами. Из таблицы 15.5 видно, что наибольший штраф имеет строка 3. Наименьшую стоимость в этой строке имеет переменная x₃₁. Максимальное значение, которое может удовлетворить обоим ограничениям, составляет 5. Вычёркиваем первый столбец, положив значение ограничения для первой строки равным 5.

Таблица 15.6

	1	2	3	4		Штраф
1	10	2 15	20	11	15	8
2	12	7	9	20	25	2
3	4 5	14	16	18	5	2
	5	15	15	15
Штраф		5	7	7

Таблица 15.7

	1	2	3	4		Штраф
1	10	2 15	20	11	0	9
2	12	7	9 15	20	25	11
3	4 5	14	16	18	5	2
	5	15	15	15
Штраф			7	7

Таблица 15.8

	1	2	3	4		Штраф
1	10	2 15	20	11 0	0	9
2	12	7	9 15	20 10	10	11
3	4 5	14	16	18 5	5	2
	5	15	15	15
Штраф			7	7

Продолжая действовать аналогично (табл. 15.6, 15.7, 15.8), получаем начальное базисное решение: x₁₂ = 15, x₁₄ = 0, x₂₃ = 15, x₂₄ = 10, x₃₁ = 5, x₃₄ = 5. Соответствующее значение целевой функции z = 475. В данном случае значение целевой функции такое же, как и при использовании метода наименьшей стоимости. Но обычно метод Фогеля даёт наилучшее начальное решение для транспортной задачи.

После определения начального базисного решения применяется алгоритм, позволяющий найти оптимальное решение транспортной задачи.

1. С помощью симплекс-критерия I определяется вводимая в базис переменная. Если в соответствии с критерием оптимальное решение достигнуто, то алгоритм завершается.

2. С помощью симплекс-критерия 2 определяется переменная, исключаемая из базиса. Происходит изменение базиса и возврат к первому этапу.

Определение вводимой в базис переменной производится с использованием метода потенциалов, с помощью которого определяются коэффициенты целевой функции, соответствующие небазисным переменным. В методе потенциалов каждой строке i и столбцу j ставится в соответствие числа (потенциалы) u_i и v_j, удовлетворяющие условию

Рассмотрим решение задачи с элеваторами. В качестве начального возьмём решение, полученное методом северо-западного угла (табл.15.9).

Таблица 15.9

	1	2	3	4
1	10 5	2 10	20	11	15
2	12	7 5	9 15	20 5	25
3	4	14	16	18 10	10
	5	15	15	15

В задаче имеется 7 неизвестных переменных (потенциалов) и 6 уравнений, соответствующих 6 базисным переменным. Для того, чтобы найти значения потенциалов из этой системы уравнений, нужно присвоить одному из них произвольное значение (обычно полагают u₁ = 0), и затем последовательно вычислять значения остальных потенциалов. Потенциалы определяются в таблице 15.10.

Таблица 15.10

Базисные переменные	Уравнения для потенциалов	Решение
x11	u1+v1 = 10	v1 = 10
x12	u1+v2 = 2	v2 = 2
x22	u2+v2 = 7	u2 = 5
x23	u2+v3 = 9	v3 = 4
x24	u2+v4 = 20	v4 = 15
x34	u3+v4 = 18	u3 = 3