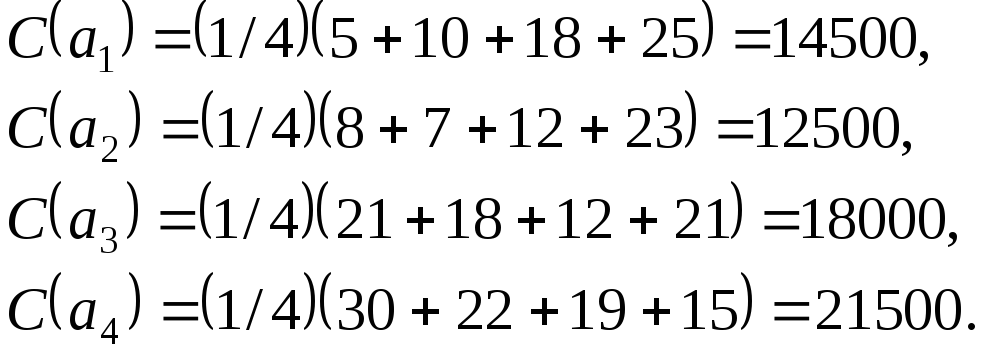16.3 Принятие решений в условиях неопределённости

Принятие решений в условиях неопределённости, как и в условиях риска, требует определения альтернативных действий, которым соответствуют платежи, зависящие от случайных состояний природы. Матрицу платежей в задаче принятия решений с m возможными действиями и n состояниями природы моно представить в виде:

где a_i – i-е возможное решение, s_j – j-е состояние природы. Плата (или доход), связанная с решением a_i и состоянием s_j равна v(a_i,s_j).

Отличие между принятием решений в условиях риска и неопределённости состоит в том, что в условиях неопределённости вероятностное распределение, соответствующее состояниям s_j, j=1,2,…,n либо неизвестно, либо не может быть определено. Этот недостаток обусловил развитие следующих критериев для анализа ситуации, связанной с принятием решения:

1. критерий Лапласа;

2. минимаксный критерий;

3. критерий Сэвиджа;

4. критерий Гурвица.

Эти критерии отличаются по степени консерватизма, который проявляет лицо, принимающее решение, в условиях неопределённости.

Критерий Лапласа опирается на принцип недостаточного обоснования, который гласит, что поскольку распределение вероятностей p(s_j) неизвестно, то нет причин считать их различными. Поэтому делается оптимистическое предположение о том, что вероятности всех состояний природы равны между собой, то есть p(s₁)=p(s₂)=...=p(s_n) = 1/n.Наилучшим является решение, которое обеспечивает максимальный выигрыш

(16.2)

или минимальные затраты

(16.3)

Максиминный или минимаксный критерий основан на выборе наилучшей альтернативы из наихудших. Если v(a_i,s_j) представляет собой получаемую прибыль, то в соответствии с максиминным критерием в качестве оптимального выбирается следующее решение:

(16.4)

Если величина v(a_i,s_j) описывает потери, то используется минимаксный критерий оптимальности решения:

(16.5)

Критерий Сэвиджа стремится смягчить консерватизм минимаксного (максиминного) критерия путём замены матрицы платежей на матрицу потерь

(16.6)

Пусть имеется матрица платежей v(a_i,s_j):

По критерию минимакса оптимальное решения – a₂. Используем теперь матрицу потерь r(a_i,s_j).

Теперь в соответствии с минимаксным критерием нужно выбрать альтернативу a₁.

Критерий Гурвица охватывает ряд различных подходов к решению – от наиболее оптимистического до наиболее пессимистического. Пусть 0 ≤ α ≤ 1, а v(a_i,s_j) представляет прибыль, получаемую при решении. Тогда в соответствии с критерием Гурвица оптимальным решением считается

(16.7)

Параметр α называется показателем оптимизма. Если α = 0, критерий Гурвица становится консервативным, так как его применение эквивалентно применению обычного минимаксного критерия. Если α = 1, критерий Гурвица становится слишком оптимистичным, так как рассчитывает на наилучшие из наихудших условий. При отсутствии ярко выраженной склонности к оптимизму или пессимизму выбирают α = 0,5.

(16.8)

Рассмотрим пример, иллюстрирующий применение всех четырёх критериев. Пусть некоторая компания планирует устроить летний лагерь. Необходимо определить размер лагеря. Если он будет слишком большим, то не окупит затрат, а если слишком маленьким, то не все желающие смогут в нём разместиться, компания не получит часть прибыли, а репутации компании будет нанесён ущерб. Считается, что число приезжающих может быть 200, 250, 300 или 350 человек. Пусть переменные a_i представляют возможные размеры лагеря, а s_i – число приехавших. Матрица стоимости описывается таблицей:

	s1	s2	s3	s4
a1	5	10	18	25
a2	8	7	12	23
a3	21	18	12	21
a4	30	22	19	15

Вычислим критерий Лапласа для этих данных. Так как вероятности всех состояний одинаковы, то вероятность каждого состояния природы равна 1/4. Величины критерия для каждой строки матрицы:

Минимальные затраты по критерию Гурвица соответствуют альтернативе a₂.

Для вычисления минимаксного критерия снова рассмотрим матрицу стоимости:

	s1	s2	s3	s4	max v(ai,sj)
a1	5	10	18	25	25
a2	8	7	12	23	23
a3	21	18	12	21	21
a4	30	22	19	15	30

По критерию минимаксы минимальные затраты соответствуют третьей альтернативе.

Сформируем матрицу потерь, которая нужна для вычисления критерия Сэвиджа:

	s1	s2	s3	s4	max v(ai,sj)
a1	0	3	6	10	10
a2	3	0	0	8	8
a3	16	11	0	6	16
a4	25	15	7	0	25

По критерию Сэвиджа минимальные затраты снова соответствуют второй альтернативе.

Для использования критерия Гурвица необходимо выбрать значение параметра оптимизма α. Пусть α = 0,5, тогда

Оптимальными по критерию Гурвица с α = 0,5 являются первая или вторая альтернативы.

Рассмотрим ещё один пример. Некий студент стоит перед выбором: готовиться к экзаменам, или участвовать в вечеринке, которую его друзья планируют устроить (предполагается, что вечеринка продлится всю ночь, а наутро предстоит экзамен). Итак, имеется три альтернативы: a₁ – участвовать в вечеринке всю ночь; a₂ – половину ночи участвовать в вечеринке, а вторую половину – готовиться к экзамену; a₃ – готовиться к экзамену всю ночь. Профессор, принимающий экзамен, непредсказуем, и экзамен может быть лёгким (s₁), средним (s₂) или трудным (s₃). В таблице представлены баллы (по стобалльной системе), которые студент может получить за экзамен в зависимости от сложности экзамена и времени, затраченного на повторение.

	s1	s2	s3
a1	85	60	40
a2	92	85	81
a3	100	88	82

То есть, в отличие от предыдущего примера, оптимальное решение должно обеспечивать максимальное значение v(a_i,s_j).

Критерий Гурвица:

В соответствии с критерием Гурвица, лучше всего учиться всю ночь

Максиминный критерий:

	s1	s2	s3	min v(ai,sj)
a1	85	60	40	40
a2	92	85	81	81
a3	100	88	82	82

И снова лучше всего готовиться к экзамену всю ночь.

Критерий Сэвиджа (в таблице приведена матрица потерь):

	s1	s2	s3	min v(ai,sj)
a1	15	28	42	42
a2	8	3	1	8
a3	0	0	0	0

Так как матрица потерь показывает, какие потери понесёт лицо, принимающее решение, в случае, если не будет принято оптимальное решение, то используем критерий минимакса и получаем, что оптимальна третья альтернатива (учиться всю ночь).

Наконец, определим величину критерия Гурвица при α = 0,5:

В соответствии с критерием Гурвица снова оптимальным выбором является подготовка к экзамену в течение всей ночи.