
Элементы комбинаторики
.docЛекция №17-18
Элементы комбинаторики
1. Кортежи и декартово произведение множеств
Определение.
Пусть даны множества
![]() .
Кортежем
длины n
составленным из элементов этих множеств
называется конечная последовательность
.
Кортежем
длины n
составленным из элементов этих множеств
называется конечная последовательность
![]() ,
где для всех k
(
,
где для всех k
(![]() )
имеем
)
имеем
![]() .
Элемент
.
Элемент
![]() называется k-ой
координатой (или k-ой
координатой) кортежа
называется k-ой
координатой (или k-ой
координатой) кортежа
![]() .
.
Пример 1.
Из множеств A = {a,b,c} и B = {1,2} можно составить 6 картежей длины 2: (a,1), (a,2), (b,1), (b,2), (c,1), (c,2).
Определение.
Два кортежа равны в том и только в том случае, когда они имеют одинаковую длину, причем их координаты стоящие на местах с одинаковыми номерами равны.
Определение.
Пусть
![]() – некоторое множества. Их декартовым
произведением
называют множество состоящее из всех
кортежей вида
– некоторое множества. Их декартовым
произведением
называют множество состоящее из всех
кортежей вида
![]() ,
где
,
где
![]() ,
,
![]() .
Декартово произведение этих множеств
обозначается так
.
Декартово произведение этих множеств
обозначается так
![]() .
.
Пример.
Пусть даны два множества = {1,2,3} и B = {x,y}. Тогда
![]() ,
,
![]() .
.
Этот пример
показывает, что, вообще говоря, декартовы
произведения
![]() и
и
![]() различны, хотя они содержат одинаковое
число элементов. Различны и множества
различны, хотя они содержат одинаковое
число элементов. Различны и множества
![]() ,
,
![]() и
и
![]() – первое состоит из троек (a,b,c),
второе – из пар вида ((a,b),c),
а третье – из пар вида (a,(b,c)),
где во всех трех случаях
– первое состоит из троек (a,b,c),
второе – из пар вида ((a,b),c),
а третье – из пар вида (a,(b,c)),
где во всех трех случаях
![]() ,
,
![]() ,
,
![]() .
.
Если хотя бы одно
из множеств пусто, то считают их декартово
произведение пустым
![]() .
.
2. Основные законы комбинаторики. Правило суммы.
Пример 2.
Если на блюде лежат 7 яблока и 4 груши, то выбрать один плод можно 7+4=11 способами. В общем виде: если элемент a можно выбрать m способами, а элемент b n способами, причем любой выбор элемента a будет отличен от выбора элемента b, то выбор a или b можно сделать m+n способами. На языке теории множеств это правило формулируется следующим образом.
Теорема I.
Если пересечение
конечных множеств A
и B
пусто
![]() ,
то число элементов в их объединении
равно сумме чисел элементов множеств
A
и B:
,
то число элементов в их объединении
равно сумме чисел элементов множеств
A
и B:
![]() . (1)
. (1)
Следствие.
Если конечные
множества
![]() попарно не пересекаются, то есть если
попарно не пересекаются, то есть если
![]() при
при
![]() ,
то справедливо равенство
,
то справедливо равенство
![]() . (2)
. (2)
Рассмотрим случай, когда множества могут иметь не пустые пересечения.
Теорема II.
Для любых конечных множеств A и B верно равенство
![]() . (3)
. (3)
Формула (3) является частным случаем более общей формулы
![]()
![]()
![]() ,
(4)
,
(4)
которую называют формулой включений и исключений. При m = 3 имеем число элементов
![]() . (5)
. (5)
Пример 2.
В группе обучается 42 студента. Из них 16 участвуют в секции по легкой атлетике, 24 – в футбольной секции, 15 – в шахматной секции, 11 – в секции по легкой атлетике и в футбольной, 8 легкоатлетической и шахматной, 12 – в футбольной и шахматной, а 6 во всех трех секциях. Остальные студенты увлекаются только туризмом. Сколько туристов является туристами.
Решение.
Пусть V
– множество
всех студентов, А
– число студентов в секции по легкой
атлетике, В
– футбольной, С
– шахматной, D
– туристической. По условию имеем
![]() причем
причем
![]() .
.
n(V)=42,
n(A)=16,
n(B)=24,
n(C)
= 15, n(![]() )
= 11, n(
)
= 11, n(![]() )
= 8,
)
= 8,
n(![]() )
= 12, n(
)
= 12, n(![]() )
= 6.
)
= 6.
По формуле (5)
получаем
![]() .
.
Поэтому
![]() .
.
Ответ: туризмом занимается 12 студентов.
3. Правило произведения
Теорема 1.
Если множества A и B конечны, то число пар в их декартовом произведении равно произведению чисел элементов этих множеств.
![]() . (6)
. (6)
Доказательство.
Множество
![]() состоит из пар вида (a,b),
где
состоит из пар вида (a,b),
где
![]() ,
,
![]() .
Если
.
Если
![]() и
и
![]() ,
то эти пары можно записать в виде
следующей таблицы:
,
то эти пары можно записать в виде
следующей таблицы:

Число этих пар
равно
![]() ,
то есть
,
то есть![]() .
С помощью метода математической индукции
формула обобщается на любое число
множеств.
.
С помощью метода математической индукции
формула обобщается на любое число
множеств.
Теорема 2.
Если множества конечны, то справедливо равенство
![]() . (7)
. (7)
Пример.
Сколько номеров, состоящих из двух букв, за которыми идут 5 цифр можно составить используя 32 буквы и 10 цифр?
Решение.
Обозначим множество
из 32 букв через A,
а множество из 10 цифр через B.
Каждый номер требуемого вида является
кортежем из декартова произведения
![]() ,
,
![]() ,
,
![]() .
.
По формуле (7)
![]() .
.
Обобщение теоремы 2.
Если первую
координату кортежа длины k
можно выбрать
![]() способами, при любом выборе первой
координаты вторая выбирается
способами, при любом выборе первой
координаты вторая выбирается
![]() способами, при любом выборе первых двух
координат третья выбирается
способами, при любом выборе первых двух
координат третья выбирается
![]() способами и так далее до k-ой
координаты включительно, то общее число
полученных таким образом картежей равно
способами и так далее до k-ой
координаты включительно, то общее число
полученных таким образом картежей равно
![]()
Основные формулы комбинаторики.
1. Размещения с повторениями.
Определение.
Кортежами длины
k
составленные из элементов m
– элементного множества X
называют размещениями
с повторениями
из m
элементов по k.
Число этих кортежей обозначают
![]() (буква A
от французского слова arrangement
– размещение. Черта сверху указывает
на возможность повторения элементов).
(буква A
от французского слова arrangement
– размещение. Черта сверху указывает
на возможность повторения элементов).
![]() .
(8)
.
(8)
Пример.
Сколько пятизначных номеров можно составить из 9 цифр 1,2,3,4,5,6,7,8,9?
Решение.
Такие номера
являются кортежами длины 5, составленными
из элементов множества X
= {1,2,3,4,5,6,7,8,9}. По формуле (8) их число равно
![]() .
.
2. Размещения без повторений.
Определение
Упорядоченное
множество длины k
составленное из элементов m
– элементарного множества X
называют размещениями
без повторений
из m
элементов множества X
по k
и обозначают
![]() .
Число размещений без повторений из m
элементов по k
находится по формуле
.
Число размещений без повторений из m
элементов по k
находится по формуле
![]() . (9)
. (9)
Пример.
Сколькими способами можно выбрать из группы, состоящей из 40 студентов старосту, профорга, физорга.
Решение.
Любой такой выбор является размещением без повторений из 40 элементов по 3.
![]() .
.
3. Перестановки без повторений.
Определение.
Перестановками
без повторений из m
элементов называют размещения
без повторений
из этих элементов по m.
Число перестановок из m
элементов обозначают
![]() от французского слова permutation
– перестановка и находятся по формуле
от французского слова permutation
– перестановка и находятся по формуле
![]() . (10)
. (10)
4. Сочетания без повторений
Определение.
Будем строить из
элементов множества X
не кортежи, а подмножества. k
– элементные подмножества m
– элементного множества X
называют сочетаниями
без повторений
из элементов этого множества по k.
Их число обозначают
![]() .
От французского слова combination
– комбинация.
.
От французского слова combination
– комбинация.
![]() . (11)
. (11)
Пример.
Сколькими способами можно составить команду по бегу из четырех человек для соревнования по бегу если имеется 7 бегунов?
Решение.
![]()
Элементы комбинаторики
5. Перестановки с повторениями
Перестановкой с повторениями состава
![]() из букв
из букв
![]() называют любой кортеж длины
называют любой кортеж длины
![]() ,
в который буква
,
в который буква
![]() входит
входит
![]() раз, …, а буква
раз, …, а буква
![]() входит
входит
![]() раз. Число таких перестановок обозначают
раз. Число таких перестановок обозначают
![]() .
.
![]() . (1)
. (1)
Пример.
Кортеж (a,b,a,a,c,b,b,b,c) является перестановкой с повторениями из трех букв а, четырех букв b и двух букв с. Его состав выражается кортежем (3,4,2). Мы считаем из букв a,b,c буква a – первая, b – вторая, c – третья.
6. Сочетания с повторениями
Пусть имеются предметы m
видов и из них составляют набор, состоящий
из k – элементов. Два
таких набора считаются одинаковыми в
том и только в том случае, когда они
имеют одинаковый состав. Такие наборы
назовем сочетаниями с повторениями из
m элементов по k.
Число сочетаний с повторениями из m
элементов по k обозначим
![]() ,
,
![]() . (2)
. (2)
Пример.
Сколько наборов из семи пирожных можно составить, если в продаже имеются четыре сорта пирожных?
Решение.
![]()
Сочетания и биномиальные коэффициенты
Рассмотрим формулы
1)
![]() .
.
2)
![]() .
.
3)
![]() .
.
4) Можно показать, что
![]() .
.
Коэффициенты при каждом члене можно найти при помощи «треугольника Паскаля»
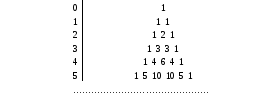
Если n
– большое число, то ясно, что по
треугольнику Паскаля вычислять
коэффициенты правой части долго. Поэтому
желательно знать общую формулу вычисления
![]() .
Эта формула носит название формулы
бинома Ньютона и имеет вид
.
Эта формула носит название формулы
бинома Ньютона и имеет вид
![]() , (3)
, (3)
где
![]() .
.
Применим формулу
бинома Ньютона для
![]()
![]() .
.
![]()
![]()
Пример.
В почтовом отделении продают открытки 10 сортов. Сколькими способами можно купить в нем: а) 12 открыток? б) 8 открыток? в) 8 различных открыток?
Решение.
а)
![]()
б)
![]()
в)
![]()
Домашнее задание.
1. У филателиста есть 8 различных марок на космическую тему и 10 различных марок на спортивную тему. Сколькими способами он сможет наклеить 3 марки одного вида и 3 марки второго вида в альбом на 6 пронумерованных мест?
2. В лаборатории работают 8 физиков и 10 химиков. Надо создать рабочие группы по трем темам. В первую группу должны войти 4 физика, во вторую 5 химиков, а третья должна состоять из 3 человека которые могут быть как физиками, так и химиками. Сколькими способами можно создать такие группы.
3. Доказать, что
![]() (правило Паскаля).
(правило Паскаля).
