
ФГБОУ ВПО Вологодская государственная молочнохозяйственная академия им. Н. В. Верещагина
Кафедра математики и механики
Курс "ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА"
(экономический факультет, очная форма обучения, направление подготовки 38.03.01 "Экономика")
Индивидуальная работа 2. ¾Случайные величины¿. Разбор типовых примеров.
Автор зав. кафедрой математики и механики, доктор физ.-мат. наук
|
Плотников М. Г. |
|
|
c |
Плотников М.Г., 2014 |
|
Содержание |
|
Содержание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . . . . 1 |
|
1. |
Дискретные случайные величины . . . . . . . . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . . . 1 |
2. |
Непрерывные случайные величины . . . . . . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . . . 4 |
3. |
Нормальное распределение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . . . 8 |
4. |
Показательное распределение . . . . . . . . . . . . . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . . 9 |
5. |
Распределение Пуассона. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . . 11 |
1. Дискретные случайные величины
Пример 1. В таблице 1 задан ряд распределения дискретной случайной величины .
Таблица 1.
|
0 |
1 |
2 |
5 |
|
|
|
|
|
P |
p1 |
0,2 |
0,4 |
0,1 |
Найти неизвестное значение p1.
Найти математическое ожидание M( ) случайной величины .
Найти моду Mo( ) величины .
Найти дисперсию D( ) и среднее квадратическое отклонение ( ) âåëè- ÷èíû .
Найти начальный 4 ( ) и центральный 4 ( ) моменты четвертого порядка величины .
Чему равна вероятность P(1 6 6 3) того, что случайная величина примет значение из отрезка [1; 3]?
1
Найти функцию распределения F (x) случайной величины и построить ее график.
Решение. Сумма вероятностей, с которыми принимает свои значения дис-
кретная случайная величина, равна единице. Другими словами, сумма чисел в нижней строке таблицы 1 равна единице:
p1 + 0; 2 + 0; 4 + 0; 1 = 1:
Отсюда p1 = 0; 3.
Математическое ожидание дискретной случайной величины находится
по формуле:
X
M( ) = xi pi;
i
ãäå xi значения величины (расположены в верхней строке таблицы 1), pi
вероятности появления соответствующих значений (расположены в нижней строке таблицы 1). В нашем случае
M( ) = 0 0; 3 + 1 0; 2 + 2 0; 4 + 5 0; 1 = 1; 5: |
(1) |
Ìîäà Mo( ) дискретной случайной величины определяется как значение (или несколько значений), которое принимается с наибольшей вероятностью. В нашем случае с наибольшей вероятностью P = 0; 4 принимается значение
x = 2, значит, Mo( ) = 2.
Дисперсию дискретной случайной величины можно найти по формуле:
|
|
|
D( ) = M 2 (M( ))2 ; |
ãäå M 2 = Xi |
xi2 pi: |
|
|
||||||||
В нашем случае |
|
|
|
|
|
|
|
|
|
|
|
|
|||
M 2 |
= 02 0; 3 + 12 0; 2 + 22 0; 4 + 52 0; 1 = 4; 3; D( ) = 4; 3 (1; 5)2 = 2; 05: |
||||||||||||||
|
|
|
квадратическое отклонение случайной величины |
|
|
||||||||||
Cреднее |
|
|
|
|
|
p |
|
|
|
|
|
находится по |
|||
формуле |
|
p |
. В нашем случае |
|
|
|
|
. |
|
|
|||||
|
|
|
|
|
|
||||||||||
Äëÿ |
|
|
|
k начальный k ( ) и центральный k ( ) моменты |
|||||||||||
|
|
( ) = D( ) |
|
|
|
( ) = 2; 05 |
1; 43 |
|
|
|
|||||
|
|
натурального числа |
|
|
|
|
|
|
|
|
|
||||
k-ого порядка случайной величины определяются формулами |
|
|
|||||||||||||
|
k ( ) = M( k) = Xi |
xik pi; |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
k ( ) =M j M( )jk = Xi |
jxi M( )jk pi: |
(2) |
||||||||
Подставляя в (2) k = 4, значения величины и соответствующие вероятности, а также найденное в (1) значение M( ), получим:
4 ( ) = 04 0; 3 + 14 0; 2 + 24 0; 4 + 54 0; 1 = 12; 85;
4 ( ) = j0 1; 5j4 0; 3 + j1 1; 5j4 0; 2 + j2 1; 5j4 0; 4 + j5 1; 5j4 0; 1 = = 16; 5625:
2

Отрезку [1; 3] принадлежат два значения случайной величины : = 1 è
= 2. Поэтому
P(1 6 6 3) = P( = 1) + P( = 2) = 0; 2 + 0; 4 = 0; 6:
Функция распределения F (x) случайной величины определяется как
F (x) = P( 6 x);
то есть значение функции F в точке x есть вероятность того, что случайная
величина примет значение, меньшее x. Построим функцию F (x), для чего рассмотрим несколько случаев.
Åñëè x < 0, òî F (x) = 0. Действительно, событие 6 x ïðè x < 0 невозможно (ведь все значения величины больше или равны 0), следовательно, его вероятность равна 0.
Åñëè 0 6 x < 1, òî F (x) = 0; 3. Действительно, если x удовлетворяет неравенству 0 6 x < 1, òî F (x) равно вероятности события 6 x, которое может произойти только когда примет значение 0 (с вероятностью 0; 3).
Åñëè 1 6 x < 2, òî F (x) = 0; 3 + 0; 2 = 0; 5. Действительно, если x удовле-
творяет неравенству 1 6 x < 2, òî F (x) равно вероятности события 6 x, которое складывается из двух событий: первое, когда примет значение 0 (с вероятностью 0; 3); второе, когда примет значение 1 (с вероятностью 0; 2). Эти два события несовместны, поэтому вероятность их суммы равна сумме их вероятностей: 0; 3 + 0; 2 = 0; 5.
Åñëè 2 6 x < 5, òî F (x) = 0; 3 + 0; 2 + 0; 4 = 0; 9. Действительно, если x
удовлетворяет неравенству 2 6 x < 5, òî F (x) равно вероятности события6 x, которое складывается из трех событий: первое, когда примет значе- ние 0 (с вероятностью 0; 3); второе, когда примет значение 1 (с вероятностью 0; 2); третье, когда примет значение 2 (с вероятностью 0; 4). Эти три события попарно несовместны, поэтому вероятность их суммы равна сумме их вероятностей: 0; 3 + 0; 2 + 0; 4 = 0; 9.
Åñëè 5 6 x, òî F (x) = 1. Действительно, событие 6 x ïðè 5 6 x достоверно (ведь все значения случайной величины меньше или равны 5), следовательно, его вероятность равна 1.
Итак, функция распределения аналитически может быть записана так:
|
|
80; 3 |
ïðè 0 |
|
x < 1; |
|
|
|
|
> |
0 |
ïðè x < 0; |
|
||
|
|
|
|
6 |
|
|
|
|
|
> |
|
|
|
|
|
F |
(x) = |
>0; 5 |
ïðè 1 |
6 |
x < 2; |
(3) |
|
|
|
> |
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
<0; 9 |
ïðè 2 |
6 |
x < 5; |
|
|
|
|
>1 |
ïðè x |
5: |
|
||
|
|
> |
|
|
> |
|
|
|
|
> |
|
|
|
|
|
|
|
> |
|
|
|
|
|
>
>
>
:
Íà ðèñ. 1 изображен график функции F (x).
3
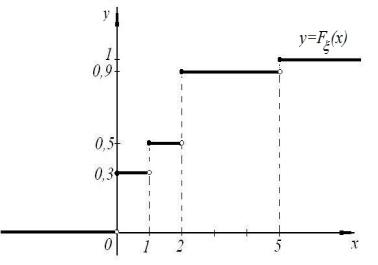
Ðèñ. 1. |
|
Ответ. p1 = 0; 3; M( ) = 1; 5; Mo( ) = 2; |
D( ) = 2; 05, ( ) 1; 43; |
4 ( ) = 12; 85, 4 ( ) = 16; 5625; P(1 6 6 3) = 0; 6; функция распределения |
|
имеет вид (3), ее график изображен на рис. 1. |
|
2. Непрерывные случайные величины
Пример 2. Непрерывная случайная величина задана плотностью распределения вероятностей
p (x) = |
8 63 |
+ |
21 |
ïðè x 2 (0; 3); |
(4) |
||
|
> |
8x2 |
10x |
|
|
||
|
|
|
|
ïðè |
|
|
|
|
< |
|
0 |
|
|
x = (0; 3): |
|
|
> |
|
|
|
|
2 |
|
|
: |
|
|
|
|
|
|
Построить график функции p (x).
Найти функцию распределения F (x) случайной величины .
Построить график функции F (x).
Найти вероятность P(0 < < 1) того, что случайная величина примет значение из интервала (0; 1).
Найти вероятность P(1 6 6 6) того, что величина примет значение из отрезка [1; 6].
Найти P( > 1).
Найти математическое ожидание M( ) случайной величины .
Решение. ментов.
Первый фрагмент соответствует значениям x 2 (1; 0], при этом y = 0. Это луч, идущий по оси Ox от начала координат бесконечно влево.
4
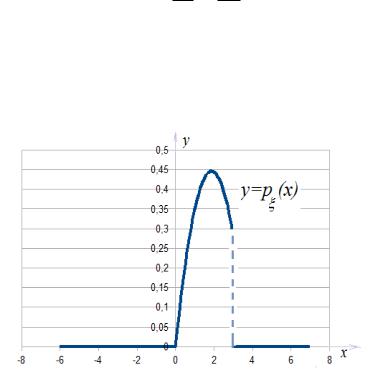
Второй фрагмент соответствует значениям x 2 (0; 3), ïðè ýòîì
y = 8x2 + 10x: 63 21
Это дуга параболы.
Третий фрагмент соответствует значениям x 2 [3; +1), ïðè ýòîì y = 0. Это луч, идущий по оси Ox бесконечно вправо от точки с координатами (3; 0).
Íà ðèñ. 2 изображен график функции p (x), построенный с помощью программы Open O ce Calc.
Ðèñ. 2.
Функция распределения F (x) связана с плотностью распределения веро-
ятности p(x) формулой
x
Z
F (x) = f(t) dt:
1
Åñëè x 6 0, òî f(t) = 0 ïðè âñåõ t 6 x è
xx
ZZ
F (x) = f(t) dt = |
0 dt = 0: |
1 |
1 |
Åñëè 0 < x < 3, òî f(t) = 0 ïðè t 6 0 è
|
f(t) = |
8t2 |
10t |
|
|
|
|||||
|
|
+ |
|
|
|
|
|
|
|
||
|
63 |
21 |
|
|
|
|
|
|
|||
ïðè t 2 (0; x). В этом случае |
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
x |
|
|
|
|||
F (x) = Z |
f(t)dt = Z |
0 dt + Z |
t2 |
10t |
dt = |
||||||
8 |
+ |
|
|
||||||||
63 |
21 |
||||||||||
1 |
1 |
|
0 |
|
|
|
|
|
|
|
|
5
|
8t3 |
5t2 |
|
x |
|
8x3 |
5x2 |
|
= 0 + |
|
0 |
= |
|||||
189 + |
21 |
189 + |
21 : |
Пусть 3 6 x. Тогда f(t) = 0 ïðè t 6 0;
f(t) = 8t2 + 10t 63 21
ïðè t 2 (0; 3); f(t) = 0 ïðè t > 3. В этом случае
|
x |
|
|
|
0 |
|
|
|
|
3 |
|
|
|
8t2 |
|
|
|
|
|
x |
|
||||
F (x) = Z |
f(t) dt = Z |
0 dt + Z |
10t |
dt + Z 0 |
dt = |
||||||||||||||||||||
|
+ |
|
|||||||||||||||||||||||
63 |
21 |
||||||||||||||||||||||||
1 |
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||
|
|
|
|
= 0 + |
8t3 |
|
5t2 |
3 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
+ 0 = |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
189 + |
|
|
21 0 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 33 |
5 32 |
|
|
8 03 |
|
|
5 |
02 |
|
|
8 15 |
|
|
||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
||||
|
+ |
|
|
|
+ |
|
|
+ |
|
= 1: |
|||||||||||||||
189 |
21 |
189 |
|
21 |
7 |
7 |
|||||||||||||||||||
В итоге функция распределения аналитически может быть записана так:
|
8 |
|
|
|
ïðè x 6 0; |
|
F (x) = |
> |
8x3 |
0 |
|
(5) |
|
> |
+ 5x2 |
ïðè 0 < x < 3; |
||||
|
> |
|
|
|
|
|
|
< |
|
|
|
|
|
|
> |
|
|
|
|
|
|
189 |
21 |
|
|
||
|
> |
|
|
|
|
|
>
>
>
:1 ïðè x > 3:
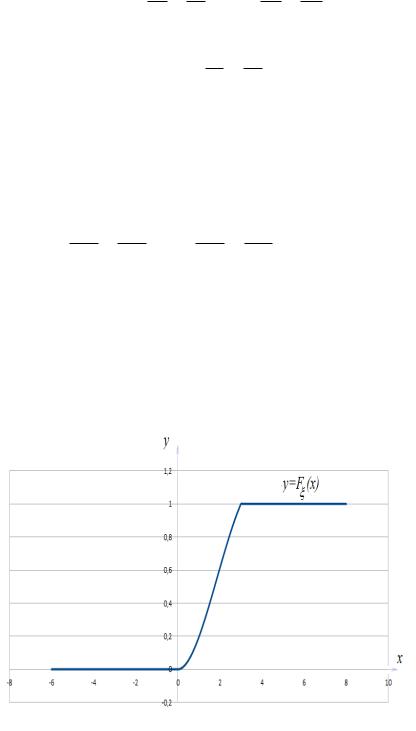
Íà ðèñ. 3 изображен график функции p (x), построенный с помощью программы Open O ce Calc.
Ðèñ. 3.
6

|
Вероятность P(a < < b) того, что непрерывная случайная величина |
|
|||||||
принимает значения из интервала (a; b), находится так: |
|
|
|
|
|||||
|
P(a < < b) = F (b) F (a): |
(6) |
|||||||
В нашем случае |
|
|
|
|
|
|
|
|
|
|
8 |
13 |
12 |
37 |
|
|
|||
|
P(0 < < 1) = F (1) F (0) = |
|
+ |
5 |
0 = |
|
: |
|
|
|
189 |
21 |
189 |
|
|||||
|
Вероятность P(a 6 6 b) того, что непрерывная случайная величина |
|
|||||||
принимает значения из отрезка [a; b], åñòü |
|
|
|
|
|
|
|
||
P(a 6 6 b) = F (b) F (a):
В нашем случае
P(1 6 6 6) = F (6) F (1) = 1 |
8 |
13 |
|
5 |
12 |
= 1 |
37 |
|
152 |
|
||
|
+ |
|
|
|
= |
|
|
: |
||||
189 |
|
21 |
189 |
189 |
||||||||
Вероятность P(a < < b) того, что непрерывная случайная величина принимает значения из интервала (a; b), находится по формуле (6). В нашем случае
P( > 1) = P(1 < < +1) = F (+1) F (1) =
= 1 |
8 |
13 |
|
5 |
12 |
= 1 |
37 |
|
152 |
|
|
|
+ |
|
|
|
= |
|
: |
||||
189 |
|
21 |
189 |
189 |
|||||||
Математическое ожидание M( ) случайной величины находится по формуле
|
+1 |
|
M( ) = |
Z |
x f(x)dx: |
|
1 |
|
Подставляя из условия плотность распределения вероятности, получаем
0 |
|
|
|
3 |
|
|
x2 |
|
10x |
|
|
|
1 |
|
|
|
M( ) = Z |
x 0 dx + Z x |
8 |
+ |
|
dx + Z x 0 dx = |
|||||||||||
63 |
21 |
|||||||||||||||
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
x3 |
10x2 |
|
|
|
|
|
|
|
8x4 |
10x3 |
3 |
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
= 0 + Z |
dx + 0 = |
0 |
|
|||||||||||||
8 |
+ |
|
|
+ |
|
= |
||||||||||
63 |
21 |
252 |
63 |
|||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 252 + |
|
|
|
|
|
|
|
|
|
|
||||
|
|
63 |
= |
7 : |
|
|
|
|
||||||||
|
|
|
|
834 |
|
1033 |
|
12 |
|
|
|
|||||
Ответ. График функции p (x) изображен на рис. 2; функция распределения
F (x) имеет вид (5); график функции F (x) изображен на рис. 3; |
P(0 < < |
1) = 37=189; P(1 6 6 6) = 152=189; M( ) = 12=7. |
|
7
