
- •Розділ 1. Теоретичні основи управління фінансовими потоками комерційного банку
- •Статистика по депозитам за лютий та березень 2014 року
- •Статистика по кредитам за лютий та березень 2014 року
- •1.2. Аналіз руху фінансових потоків
- •Розділ 2. Методи і моделі управління фінансовими потоками комерційного банку
- •2.1. Аналіз основних методів та схема моделей фінансових потоків комерційного банку
- •Вони підходять для починаючих вивчати імітаційне моделювання
- •1. Імітаційна системно-динамічна моделі потоків комерційного банку, що дозволяє реалізувати етап 1.
- •2.3. Економетричні моделі на базі регресійного аналізу та аналізу часових рядів
- •Розділ 3. Моделювання фінансових потоків комерційного банку на прикладі пат «приватбанк»
- •3.1 Аналіз банків України та імітаційна модель фінансових потоків пат «приватбанк»
- •Власний капітал банків України на 01.01.2014 року, тис. Грн.
- •Види змінних
- •3.2. Економетричне моделювання фінансових потоків пат «приватбанк»
- •Характеристики, види залежності та процедури лінеаризації
- •Розділ 4. Забезпечення охорони праці та техніки безпеки на об’єкті фінансового відділу пат «приватбанк»
- •4.1. Аналіз санітарно-гігієнічних умов праці в приміщенні фінансового відділу пат «приватбанк»
- •Параметри санітарно-гігієнічних умов праці в приміщенні фінансового відділу пат «приватбанк»
- •4.2. Техніка безпеки в приміщенні фінансового відділу пат «приватбанк»
- •Висновки
- •Список використаних джерел
Характеристики, види залежності та процедури лінеаризації
|
Характеристика |
Вид залежності |
Процедура лінеаризації |
|
1 |
2 |
3 |
|
перші, другі, …, m-ті різниці:
|
полиноми відповідно першого, другого, …, m-ого ступеня:
|
заміна
|
|
темпи
росту:
|
показникові функція:
|
логарифмування
обох частин рівняння і заміна
дозволить представити
модель у виді:
|
|
перші різниці зворотних значень рівнів wt(1)=zt+1-zt |
зворотна функція:
|
заміна
|
|
перші прирости логарифмів рівнів
|
степенева (мультиплікативна) функція:
|
логарифмування обох
частин рівняння та заміна |
Розглянемо процедуру лінеаризації для показникової функції.
Для лінеаризації застосовуємо процедуру
логарифмування:![]() .
Робимо заміни:
.
Робимо заміни:
![]() ,
,
![]() ,
,
![]() .
Отримаємо лінійну форму моделі:
.
Отримаємо лінійну форму моделі:
![]() .
За допомогою аналізу даних зокрема
регресії на рис. 3.11. отримуємо а0=9,47 та
а1=0,042, по критерію Стьюдента – параметри
статистично значимі, тому що t-статистика
більше табличного значення,
вірогідність помилки статистичної
теорії менше ніж 0,05,
лінійна форма моделі матиме вигляд:
.
За допомогою аналізу даних зокрема
регресії на рис. 3.11. отримуємо а0=9,47 та
а1=0,042, по критерію Стьюдента – параметри
статистично значимі, тому що t-статистика
більше табличного значення,
вірогідність помилки статистичної
теорії менше ніж 0,05,
лінійна форма моделі матиме вигляд:
y*=9,47+0,042*t, (3.3)

Рис. 3.11. Результати аналізу регресії
Розрахунки показникової моделі показані на рис. 3.12.

Рис. 3.12. Модель тренду показникової функції
Будуємо прогнозну модель використовуючи знайдені параметри а0 і а1 для тренда і отримуємо середню абсолютну процентну помилку – 5%.
Для того, щоб візуально порівняти вихідні дані та збудований тренд побудований графік на рис. 3.13. з вихідними даними і трендом

Рис. 3.13. Графік тренду та вихідних даних
Наступним кроком необхідно лінеаризувати степеневу функцію використовуючи таблицю 3.4.
![]()
![]() ,
,
![]() ,
,
![]()
За допомогою вбудованої функції в екселі – аналізу даних регресії , результат можна бачити на рис. 3.14. отримуємо параметри а0=9,39 та а1=0,21, параметри статистично значимі.

Рис. 3.14. Результати аналізу регресії
Розрахунки степеневої моделі показані на рис. 3.15.

Рис. 3.15. Модель тренду степеневої функції
Mape – усього 3%, різницю між степеневою та показниковою можна побачити на рис. 3.16.

Рис. 3.16. Графік за вихідними даними та моделями тренду степеневої і показникової функцій
Кінцева функція завдання власного капіталу виглядає:
Y=11993.5*(Time+12)^0.21, (3.4)
де Time – время.
Вона використовується для завдання власного капіталу як додаткову змінну для прогнозування на наступний рік, тому що дотримані два припущення які дозволяють нам використовувати метод екстраполяції:
-
часовий ряд економічного показника дійсно має тренд, тобто переважну тенденцію;
-
загальні умови, що визначали розвиток показника минулого, залишаться без істотних змін протягом періоду попередження.
Ці рівняння є частиною складної імітаційної моделі. Аналіз регресії показав, що є зв'язок між кредитом та депозитом, тому завдаючи прогноз кредиту на основі депозиту можливо управляти динамікою кредитів через депозити. Для цього необхідно змінювати параметри зняття і поповнення депозитів, і проаналізувавши експерименти прийняти управлінські рішення.
3.3. Аналіз та оптимізація фінансових потоків комерційного банку на базі економіко-математичних моделей
Для того, що спрогнозувати динаміку фінансових потоків комерційного банку, проведемо імітаційний експеримент з моделлю. Для цього в Vensim запустимо модель при початкових даних таких:
Початковий час дорівнює – 1, кінцевий – 4, крок це квартал, що дозволяє прослідкувати динаміку за наступний рік.
Запустимо нашу імітаційну модель, вона показана на рис. 3.17.

Рис. 3.17. Імітаційна модель балансу у Vensim
Власний капітал зростає згідно свого тренду на рис. 3.18.

Рис. 3.18. Графік динаміки власного капіталу
На рис. 3.19. можна побачити залежність кредита від депозиту:

Рис. 3.19. Графіки залежності кредиту від депозиту
Як видно кредит дуже різко реагує на будь які зміну в депозитах, це означає щоб вплинути на тенденцію кредиту достатньо трохи змінити динаміку депозитів та вже можна побачити істотні зміни.
Подивимось на динаміку поточної ліквідності на рис. 3.20.

Рис. 3.20. Динаміка поточної ліквідності
Рекомендований коефіцієнт повинен коливатись у межах від 0,4 до 1. Тому досліджуваний банк має дуже високу платоспроможність.
Наступним кроком прослідкуємо динаміку ліквідності в залежності від вхідних у неї змінних на рис. 3.21.

Рис. 3.21. Графіки кредиту, зобов’язань та залежної від них ліквідності
На графіках видно, що ліквідність у рівній мірі залежить як від зобов'язань, так і від здатності їх погасити.
Отже, для оптимізації руху грошових коштів, проведемо декілька прогонів моделі, використовуючи модель планування імітаційного експерименту зі зміною факторів по одному.
Характер експериментів:
-
Base – зняття та поповнення депозиту відбувається за допомоги функції RANDOM UNIFORM (m, x) – рівномірний розподіл на інтервалі від m до x, змінні вкладення та зняття рахуються як RANDOM UNIFORM (1, 133551) де 133551 – данні по депозиту за останній квартал та початкове значення для змінної рівня – Deposit.
-
Current – змінна вкладення депозиту рахується як RANDOM UNIFORM (1, 66776), де 66776 – половина від вихідних даних, що дозволяє подивитися на динаміку депозиту при рівні вкладень зниженому у 2 рази, змінна зняття незмінна.
-
Current1 – змінна зняття депозиту рахується як RANDOM UNIFORM (1, 66776), що дозволяє подивитися на динаміку депозиту при рівні зняття зниженому у 2 рази, змінна вкладення – RANDOM UNIFORM (1, 133551).
Нижче наведемо результати прогонів моделі, зокрема по депозиту на рис. 3.22.

Рис. 3.22. Динаміка депозиту протягом експериментів
Як видно зменшення зняття депозитів з рахунків набагато покращує динаміку рівня депозиту в цілому, у той час як збільшення вкладень впливає незначною мірою. Тобто, управління «Приватбанк» повинно приділяти більш уваги до збереженню довіри до банку та існуючих клієнтів, ніж проведенню реклами та розробки маркетингових стратегій задля залучення нових резидентів.
Динаміка ліквідності протягом експериментів показана на рис. 3.23.

Рис. 3.23. Динаміка ліквідності
Цю ж думку підтверджує рис. 3.24 та рис. 3.25 з графіками динаміки ліквідності та її залежності від змінних кредиту та зобов’язань, на якому ліквідність зазнає серйозне падіння у другому експерименті, а в третьому навпаки. Тобто, зниження рівню вкладення депозитів серйозно зменшує платоспроможність банку до критичного рівня ліквідності менше 0,4.

Рис. 3.24. Графік динаміки ліквідності
З цього можна зробити висновок, що взявши за критерій по оптимізації коефіцієнт поточної ліквідності необхідно зменшувати кількість зняття з депозиту.

Рис. 3.25. Графіки кредиту, зобов’язань та залежної від них ліквідності протягом експериментів
Динаміка кредиту істотно варіюється залежно від кількості депозитів на рахунках на рис. 3.26.

Рис. 3.26. Динаміка кредиту протягом експериментів
Графік динаміки балансу можна подивитись на рис. 3.27.

Рис. 3.27. Динаміка балансу протягом експериментів
Можна зробити висновок, що оптимізуючи фінансові потоки ПАТ «ПРИВАТБАНК» за всіма основними критеріями такі як: кількість депозитних вкладень, взятих кредитів, рівень поточної ліквідності, отримано певні управлінські рішення. Управління «Приватбанк» повинно приділяти більш уваги до збереженню довіри до банку та існуючих клієнтів вводячи всілякі акції та систему заохочення постійних клієнтів, ніж проведенню реклами та розробки маркетингових стратегій задля залучення нових резидентів. Це призведе до збереження більшої частини поточних резидентів, з невеликими втратами у вигляді зменшення відсотка появи нових клієнтів.

 ;
;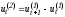 ;
…
;
… .
.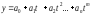
 ,
,
 ,
… ,
,
… ,
 дозволить
представити модель у виді:
дозволить
представити модель у виді:


 ,
,
 ,
,



 дозволить представити модель у виді:
дозволить представити модель у виді:


 ,
,
 ,
,
 дозволить представити модель у виді:
дозволить представити модель у виді:
