инд. задание 1

Одержано базисний розв’язок . Для перевірки підставимо одержаний розв’язок, наприклад, в останнє рівняння системи:

.

Приклад 5. Довести, що вектори , , , утворюють базис і знайти координати вектора в цьому базисі.

Розв’язок. Доведемо, що вказані вектори утворюють базис, для чого покажемо їхню лінійну незалежність. Складемо векторну рівність , яка в координатній формі приводить до системи однорідних лінійних алгебраїчних рівнянь:

, розв’язуючи яку методом Жордану – Гаусса, одержують єдиний тривіальний розв’язок . Таким чином, вектори , , , утворюють базис. Розкладемо вектор в цьому базисі: . Після запису одержаного рівняння в координатній формі та розв’язання системи рівнянь в новому базисі вектор матиме координати: , або .

Приклад 6. Задано координати точок трикутника ; ; . Знайти: а) рівняння прямої, що проходить через сторону трикутника АВ; б) рівняння прямої, яка проходить через перпендикуляр, який падає на сторону АВ з вершини С; в) рівняння прямої, яка проходить через т. С паралельно до сторони АВ; г) відстань від т. С до сторони АВ; д) косинус кута між сторонами АВ та ВС.

Розв’язок. а) Рівняння прямої, яка проходить через дві задані точки, має вигляд , тоді рівняння сторони АВ:

,

або через кутовий коефіцієнт: .

б) Умова перпендикулярності прямих: . Для прямої АВ кутовий коефіцієнт , тоді для перпендикулярної прямої: . Рівняння прямої, яка проходить через задану точку, має вигляд . Тоді шукане рівняння прямої, яка проходить через точку С перпендикулярно до АВ:

.

в) Умова паралельності прямих: . Тоді рівняння прямої, що проходить через т. С паралельно до АВ:

.

г) Відстань від точки до прямої знаходиться за формулою:

,

де – координати нормального вектора прямої.

Запишемо рівняння прямої АВ в загальній формі: , тоді нормальний вектор прямої , .

одиниць.

д) Косинус кута між двома прямими знаходиться за формулою:

.

Знайдемо рівняння прямої, що проходить через сторону ВС:

,

нормальний вектор цієї прямої має координати: . Тоді косинус кута між прямими АВ та ВС:

.

Приклад 7. Задано координати вершин трикутної піраміди ; ; ; . Знайти: а) довжину ребра та рівняння прямої, що проходить через ; б) проекцію вектора на та кут між ними; в) площу грані ; г) рівняння висоти, медіани та бісектриси, проведених з кута на грані ; д) об’єм піраміди; е) рівняння площини АВС; ж) рівняння та довжину висоти, яка проведена з вершини на грань .

Розв’язок. а) Знайдемо координати вектора та його модуль:

, .

Рівняння прямої : .

б) Знайдемо проекцію вектора на за формулою:

.

, .

Нехай – кут між векторами та , тоді:

.

в) Відомо, що . Знайдемо: , , (кв. од.)

г) Запишемо рівняння прямої, яка проходить через сторону . Знайдемо рівняння площини, яка проходе через точку перпендикулярно до даної прямої. За нормальний вектор цієї площини візьмемо напрямний вектор прямої :

, .

Далі знайдемо точку перетину даної площини з прямою , для чого представимо рівняння прямої в параметричній формі та підставимо його в рівняння площини:

, , , .

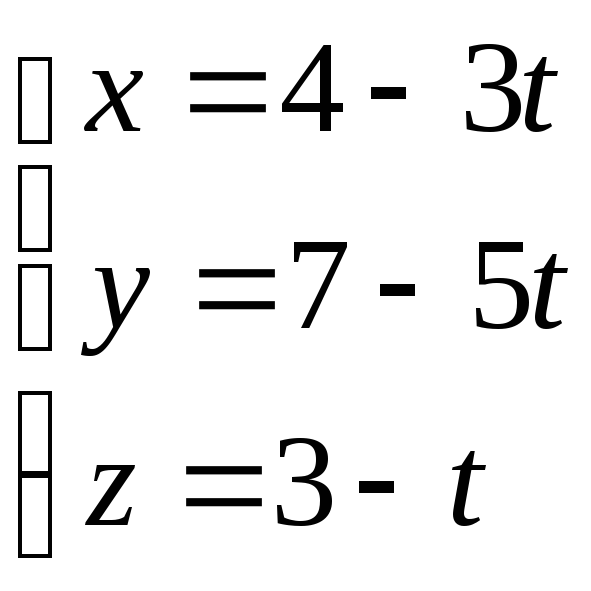Запишемо рівняння висоти : .

Знайдемо координати середини сторони :

; ; ;

тоді рівняння медіани має вигляд .

За напрямний вектор бісектриси можна взяти вектор , запишемо рівняння бісектриси :

.

д) Відомо, що , ,

, (куб. од.)

е) Знайдемо рівняння площини :

, звідки .

ж) За напрямний вектор висоти, яка проведена з вершини на площину , можна взяти нормальний вектор цієї площини , тоді маємо рівняння висоти: . Її довжина: (од.).

28