инд. задание 1
.doc
.
3.
а)
;
б)
.
4.
.
5.
6.
.
7.
;
;
;
.
Варіант 24
1.
;
. 2.
;
.
3.
а)
;
б)
.
4.
.
5.
6.
.
7.
;
;
;
.
Варіант 25
1.
;
2.
;
.
3.
а)
;
б)
.
4.
.
5.
6.
.
7.
;
;
;
.
Варіант 26
1.
;
. 2.
;
.
3.
а)
;
б)
.
4.
.
5.
6.
.
7.
;
;
;
.
Варіант 27
1.
;
. 2.
;
.
3.
а)
;
б)
.
4.
.
5.
6.
.
7.
;
;
;
.
Варіант 28
1.
;
. 2.
;
.
3.
а)
;
б)
.
4.
.
5.
6.
.
7.
;
;
;
.
Варіант 29
1.
;
. 2.
;
.
3.
а)
;
б)
.
4.
.
5.
6.
.
7.
;
;
;
.
Варіант 30
1.
;
. 2.
;
.
3.
а)
;
б)
.
4.
.
5.
6.
.
7.
;
;
;
.
Зразок виконання індивідуального завдання з теми
“Елементи лінійної та векторної алгебри”
Приклад 1. Дано
дві матриці
та
.
Знайти: а)
;
б)
;
в)
.
Розв’язок.
а)
Знайдемо спочатку
та
множенням кожного елемента матриць на
відповідний множник:
,
,
а їх сума знаходиться поелементно, тобто додаються елементи з однаковими номерами:
.
б) Множення матриці
(вимірності
)
на матрицю
(вимірності
)
можливо, коли кількість стовпців першої
матриці дорівнює кількості рядків
другої. Елементи матриці
,
яка є добутком
на
,
знаходимо за формулою:
,
де
;
.
Отже, маємо:
.
в) Знайдемо спочатку
визначник квадратної матриці
за правилом трикутника:
.
Оскільки визначник
матриці
не дорівнює нулю, то для неї існує
обернена матриця
,
яка знаходиться за формулою:
,
де
– алгебраїчні доповнення елементів
транспонованої матриці
.
Алгебраїчні доповнення знаходяться за формулою:
,
де
– мінори елементів
.
Запишемо
транспоновану матрицю
,
для якої далі знайдемо алгебраїчні
доповнення, та одержимо обернену матрицю
:
.
;
;
;
;
; 
;
; 
;
.
.
Перевіримо
правильність її знаходження. Відомо,
що
та
,
де
– одинична матриця. Дійсно,
,
аналогічно,
.
Приклад
2. Знайти визначник
:
а) розклавши його за елементами другого
рядку; б) методом ефективного зниження
порядку.
Розв’язок. а) Обчислимо визначник, розклавши його за елементами 2-го рядку
.
; 
; 
;
.
.
б) Користуючись основними властивостями визначників, можна звести обчислення визначника 4-го порядку до обчислення лише одного визначника 3-го порядку (замість чотирьох), якщо всі елементи будь-якого рядка (стовпця), крім одного, зробити рівними нулю – “метод ефективного зниження”.
Отримаємо нулі, наприклад, у третьому стовпці. Перший рядок залишимо без зміни. До елементів другого рядку додамо відповідні елементи першого, помножені на – 3. До елементів третього рядку додамо відповідні елементи першого, помножені на – 2. До елементів четвертого рядку додамо відповідні елементи першого.
можна й далі, користуючись цим методом, знижувати порядок визначника до 2-го і навіть до 1-го:
.
Приклад 3.
Розв’язати
систему рівнянь
:
а) матричним способом; б) за формулами
Крамера; в) методом Жордану – Гаусса.
Розв’язок. Перевіримо сумісність даної системи за теоремою Кронекеру – Капеллі, для чого, користуючись методом нулів та одиниць, знайдемо ранг матриці системи та ранг розширеної матриці:
.
Таким
чином,
,
система сумісна та має єдиний розв’язок.
а) Розв’язок системи матричним методом виконується за формулою:
.
Знайдемо обернену матрицю системи:
;
;
.
Тобто
розв’язок системи:
,
і
.
Перевіримо правильність розв’язання,
для чого підставимо знайдені корені,
наприклад, у друге рівняння системи:
,
.
б) За формулами Крамера
(тут
– визначник матриці системи,
– визначник, який утворюється з визначника
системи
в результаті заміни
-го
стовпця на стовпець правих частин
).
;
;
;
знаходимо:
;
;
.
в) Суть методу Жордану – Гаусса полягає в послідовному виключенні невідомих з усіх рівнянь окрім одного, провідного, і в приведенні системи до “трикутного вигляду”.
Коефіцієнти при невідомих, вільні члени та суми усіх коефіцієнтів кожного рядка (останній контрольний стовпчик таблиці) запишемо у таблицю Гаусса:
-
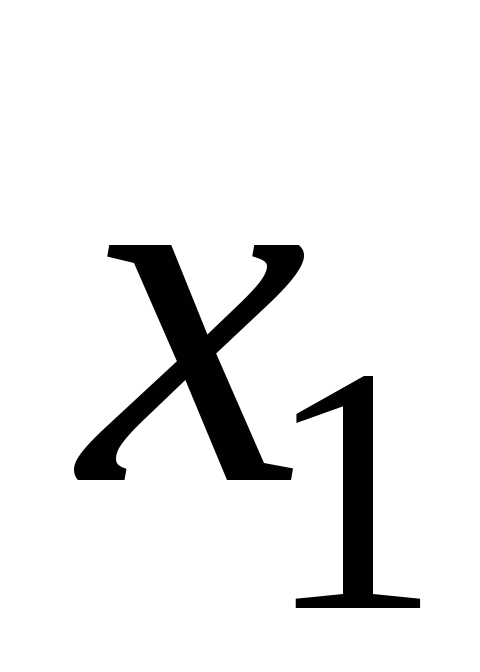
1
1
3
0
5
2
-1
2
3
6
-1
-2
-1
1
-
3
Нехай провідним стовпцем
буде стовпець при
,
а провідним елементом буде
(його взято в рамку), коефіцієнт при
невідомій в цьому випадку дорівнює
одиниці і тому не треба робити додаткових
обчислень. Після перетворень маємо:
-
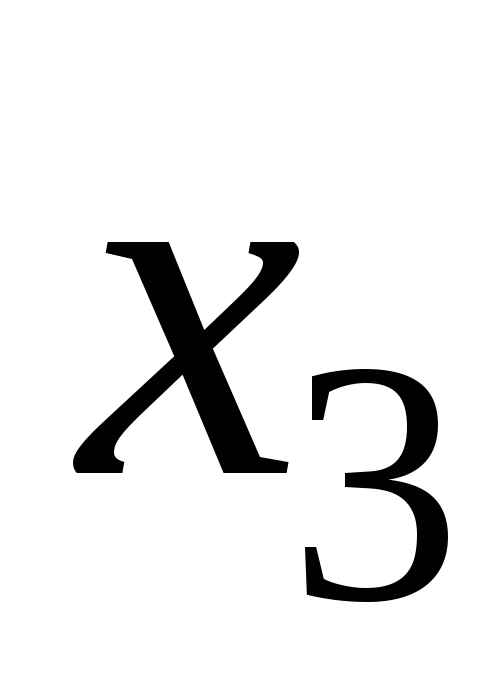
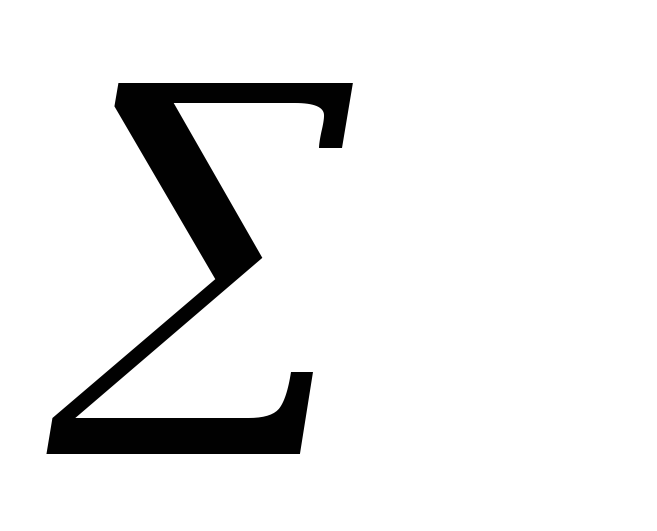
1
1
3
0
5
0
-
3-4
3
-
4
0
-1
2
1
2
Для контролю правильності перетворень просумуємо елементи кожного рядка, які стоять у перших чотирьох стовпцях, і порівняємо з елементом у останньому стовпці. Якщо вони співпадають, усі перерахування зроблено правильно.
-
1
1
3
0
5
0
1
4/3
-1
4
/30
-1
2
1
2
1
0
5/3
1
11/3
0
1
4/3
-1
4/3
0
0
1
0/30
1
0/3
1
0
5/3
1
1
1/30
1
4
/3-1
4
/30
0
1
0
1
1
0
0
1
2
0
1
0
-1
0
0
0
1
0
1
Отже
,
,
.
Як бачимо, незалежно від методу
розв’язання, одержано той самий
результат.
Приклад 4. Перевірити на сумісність систему рівнянь
і
у разі сумісності розв’язати її.
Р
озв’язок.
Перевіримо
на сумісність дану систему рівнянь:
.
-
1
-2
-1
1
0
0
-2
-3
2
0
0
1
-1
0
9
11
-3
1
0
0
1
-1
-16
-18
2
2
1
-1
0
1
23
28
1
-2
-1
1
0
0
-2
-3
0
4
2
-1
-1
0
13
17
0
-5
-3
3
1
-1
-22
-27
0
6
3
-3
0
1
27
34
1
-2
-1
1
0
0
-2
-3
0
-1
-1
2
0
-1
-9
-10
0
-5
-3
3
1
-1
-22
-27
0
6
3
-3
0
1
27
34
1
-2
-1
1
0
0
-2
-3
0
5
2
-1
0
0
18
24
0
1
0
0
1
0
5
7
0
6
3
-3
0
1
27
34
1
0
-1
1
2
0
8
11
0
0
2
-
1-5
0
-7
-11
0
1
0
0
1
0
5
7
0
0
3
-3
-6
1
-3
-8
1
0
1
0
-3
0
1
0
0
0
-2
1
5
0
7
11
0
1
0
0
1
0
5
7
0
0
-3
0
9
1
18
25