
инд. задание 1
.docВступ
Даний збірник містить шість завдань індивідуальних робіт з навчальної дисципліни “Вища математика для економістів” та одне індивідуальне навчально-дослідне завдання. Індивідуальне завдання з кожного змістовного модуля містить 30 варіантів, які обираються студентами згідно зі списком академічної групи. Після кожного індивідуального завдання міститься зразок виконання та оформлення роботи.
Матеріал у збірнику розміщено відповідно до вимог програми.
Вивчення кожного змістовного модуля закінчується захистом індивідуального завдання. Необхідною вимогою отримання студентом підсумкової екзаменаційної оцінки з дисципліни є захист всіх індивідуальних завдань.
Індивідуальне навчально-дослідне завдання призначене для студентів, які мають високий рівень навчальних досягнень.
Індивідуальні завдання з теми “Елементи лінійної та векторної алгебри”
1.
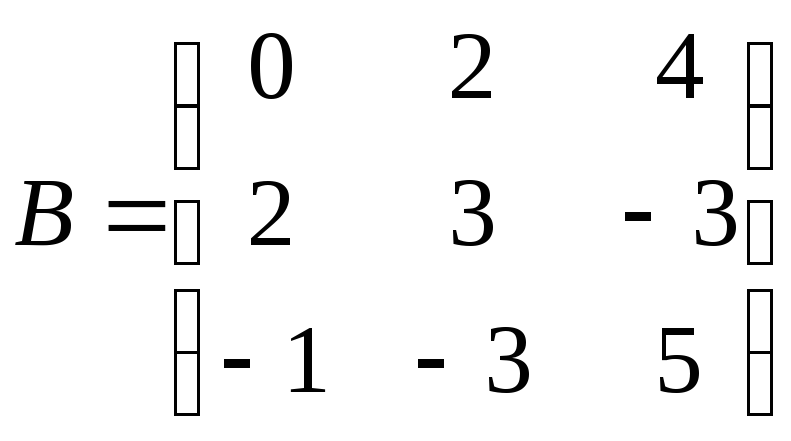
Дано дві матриці
![]() і
і
![]() .
Знайти: а)
.
Знайти: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
2.
Для даного визначника знайти мінор і
алгебраїчне доповнення елемента
![]() .
Обчислити визначник: а) розкладанням
його за елементами
.
Обчислити визначник: а) розкладанням
його за елементами
![]() -ого
рядка; б) розкладанням його за елементами
-ого
рядка; б) розкладанням його за елементами
![]() -ого
стовпця; в) отримавши нулі в
-ого
стовпця; в) отримавши нулі в
![]() -му
рядку.
-му
рядку.
3. Перевірити систему на сумісність і у разі сумісності розв’язати її: а) методом оберненої матриці, б) за формулами Крамера, в) методом Жордана – Гаусса.
4. Перевірити систему на сумісність і у разі сумісності розв’язати її.
5.
Довести, що вектори
![]() ,
,
![]() ,
,
![]() ,
,
![]() утворюють базис та розкласти вектор
утворюють базис та розкласти вектор
![]() за цим базисом.
за цим базисом.
6.
Задано координати вершин трикутника
![]() .
Знайти: а) рівняння прямої, що
проходить через сторону трикутника
.
Знайти: а) рівняння прямої, що
проходить через сторону трикутника
![]() ;
б) рівняння прямої, яка проходить через
перпендикуляр, який падає на сторону
;
б) рівняння прямої, яка проходить через
перпендикуляр, який падає на сторону
![]() з
вершини
з
вершини
![]() ;
в) рівняння прямої, яка проходить через
т.
;
в) рівняння прямої, яка проходить через
т.
![]() паралельно до сторони
паралельно до сторони
![]() ;
г) відстань від т.
;
г) відстань від т.
![]() до сторони
до сторони
![]() ;
д) косинус кута між сторонами
;
д) косинус кута між сторонами
![]() та
та
![]() .
.
7.
Задано координати вершин трикутної
піраміди
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Знайти: а) довжину ребра
.
Знайти: а) довжину ребра
![]() та рівняння прямої, що проходить через
та рівняння прямої, що проходить через
![]() ;
б) проекцію вектора
;
б) проекцію вектора
![]() на
на
![]() та кут між ними; в) площу грані
та кут між ними; в) площу грані
![]() ;
г) довжину та рівняння висоти, медіани
та бісектриси, проведених з кута
;
г) довжину та рівняння висоти, медіани
та бісектриси, проведених з кута
![]() на грань
на грань
![]() ;
д) об’єм піраміди; е) рівняння площини
;
д) об’єм піраміди; е) рівняння площини
![]() ;
ж) рівняння та довжину висоти, яка
проведена з вершини
;
ж) рівняння та довжину висоти, яка
проведена з вершини
![]() на грань
на грань
![]() .
.
Варіант 1
1.
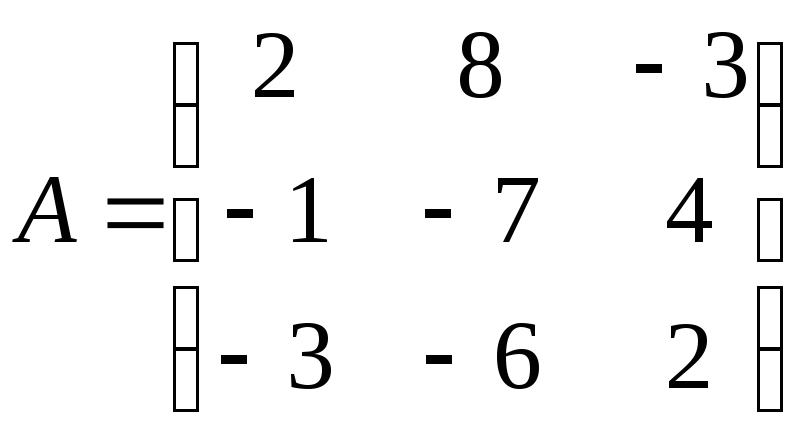 ;
;
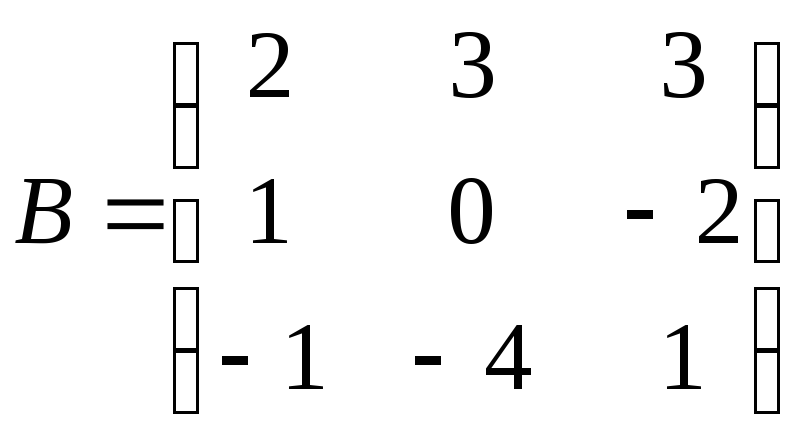 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
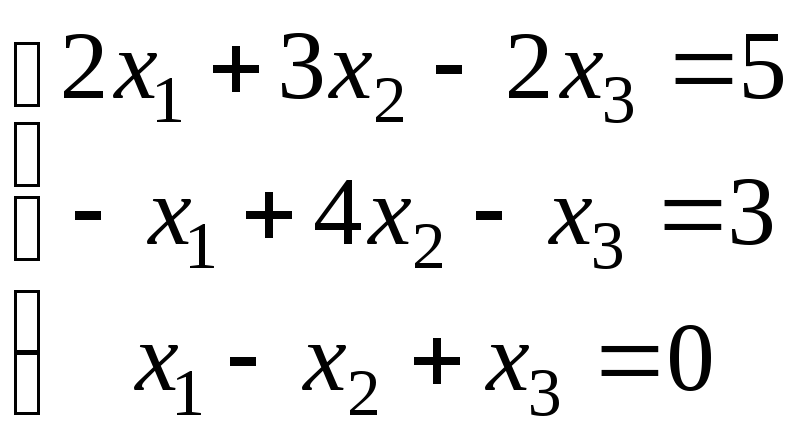 ; б)
; б)
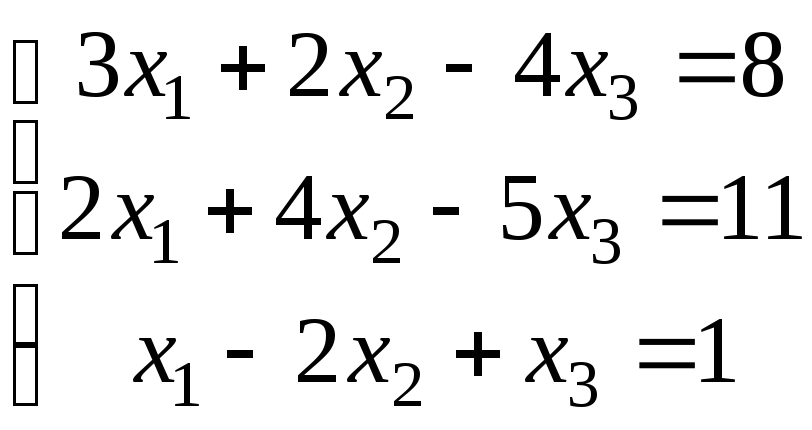 .
.
4.
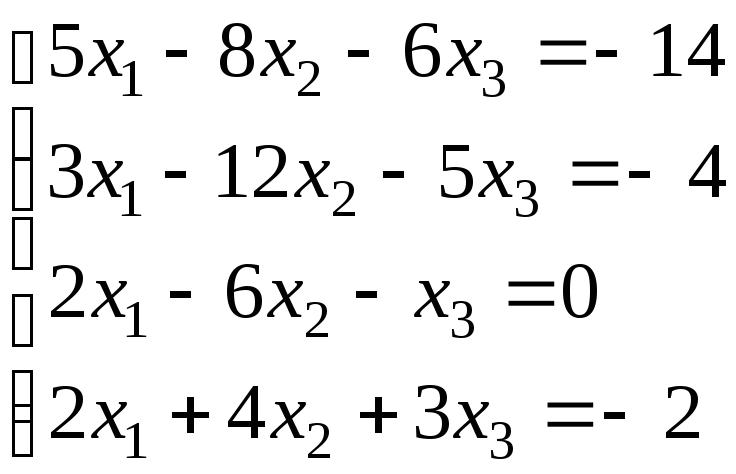 .
5.
.
5.
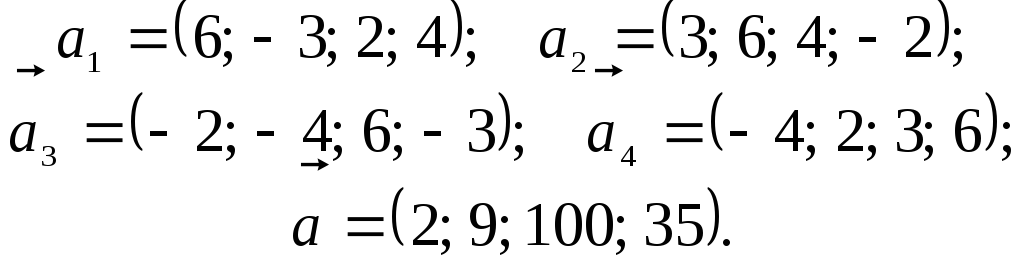
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 2
1.
 ;
;
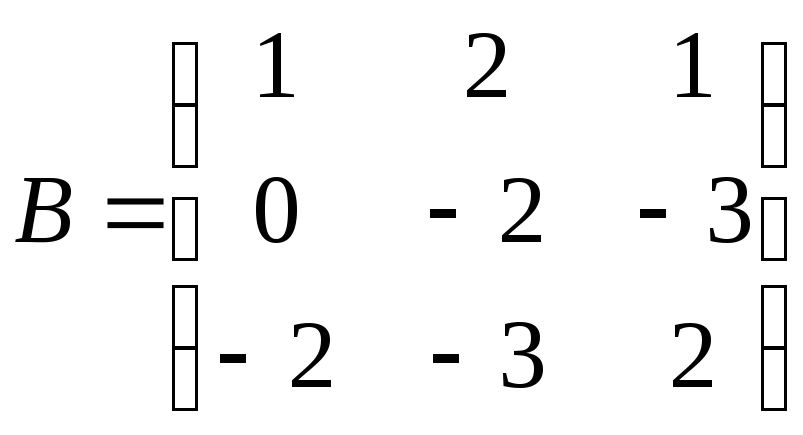 .
2.
.
2.
 ;
;
![]() .
.
3.
а)
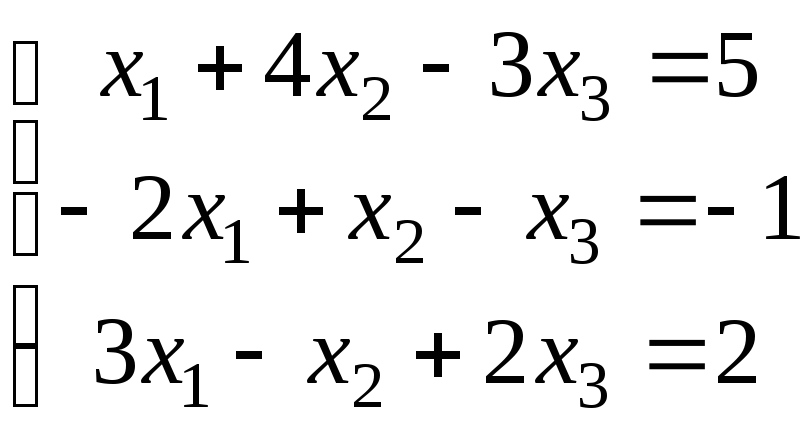 ;
б)
;
б)
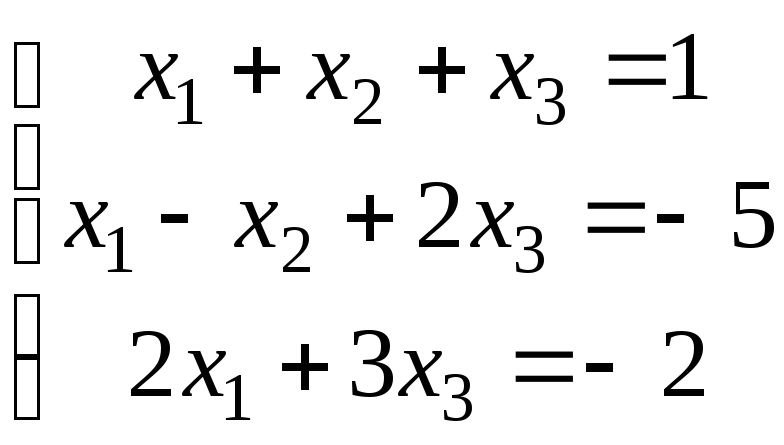 .
.
4.
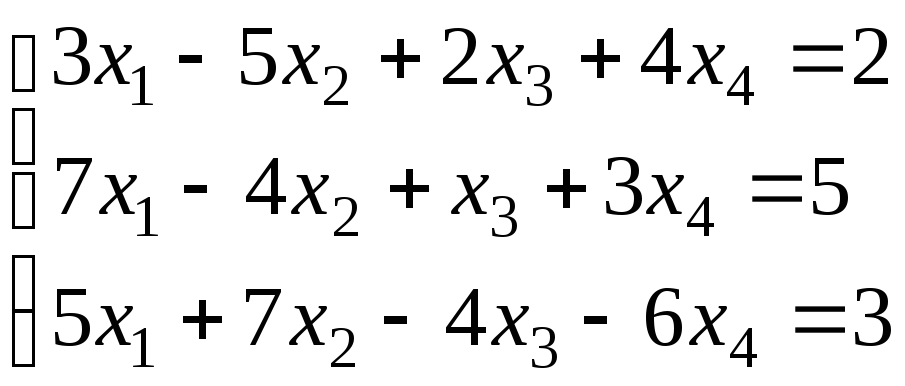 . 5.
. 5.
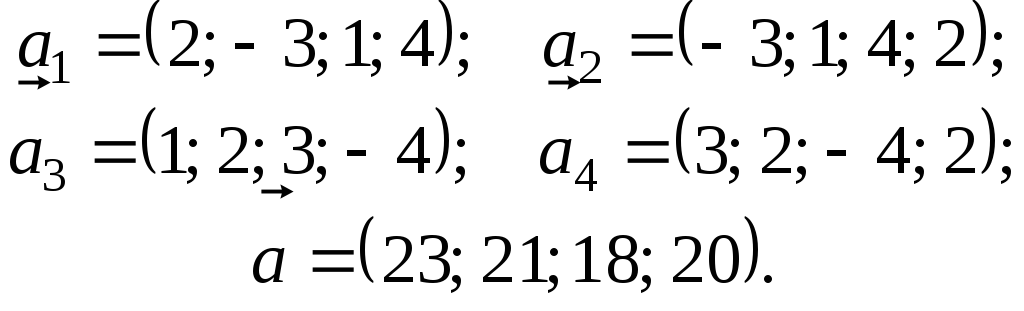
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 3
1.
 ;
;
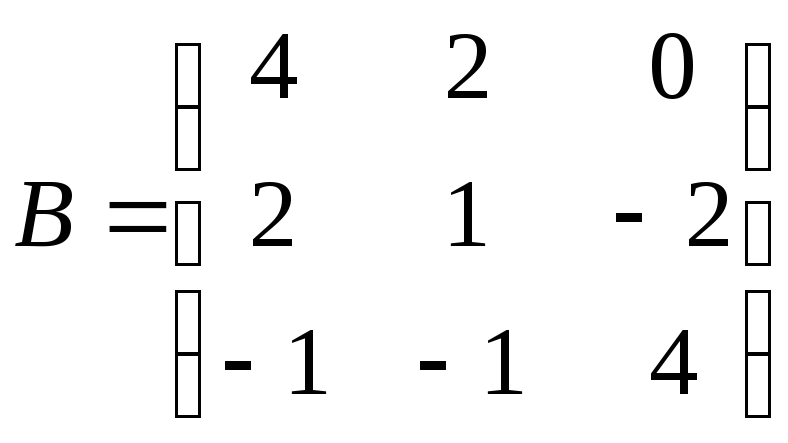 . 2.
. 2.
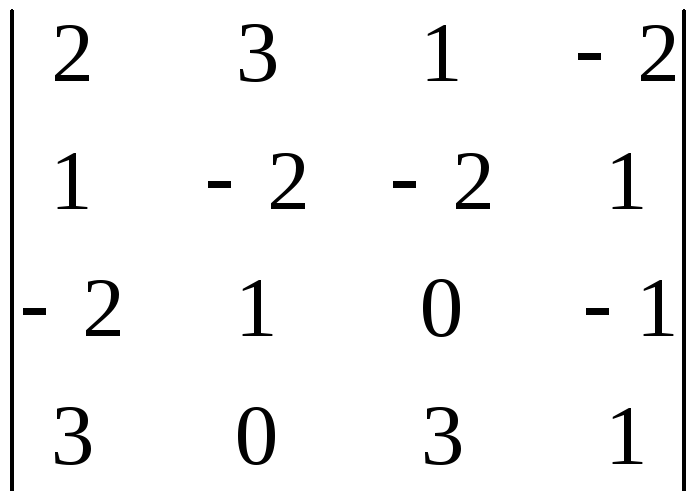 ;
;
![]() .
.
3.
а)
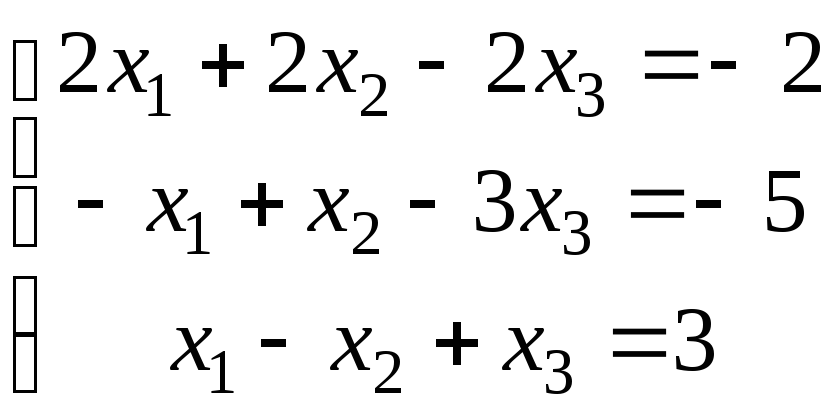 ;
б)
;
б)
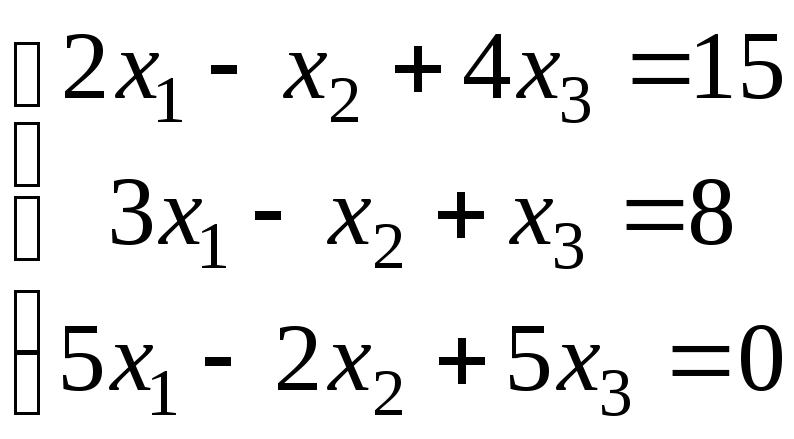 .
.
4.
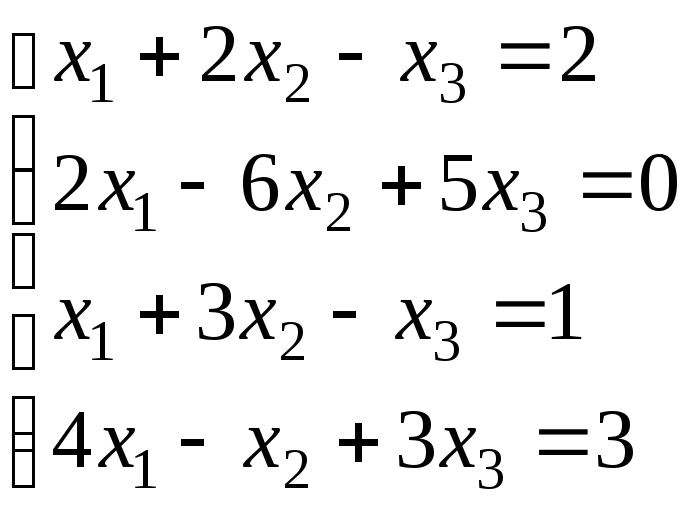 .
5.
.
5.

6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 4
1.
 ;
;
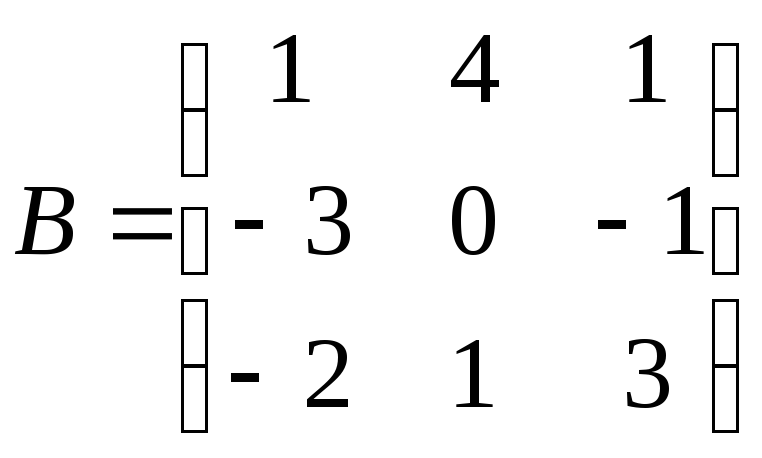 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
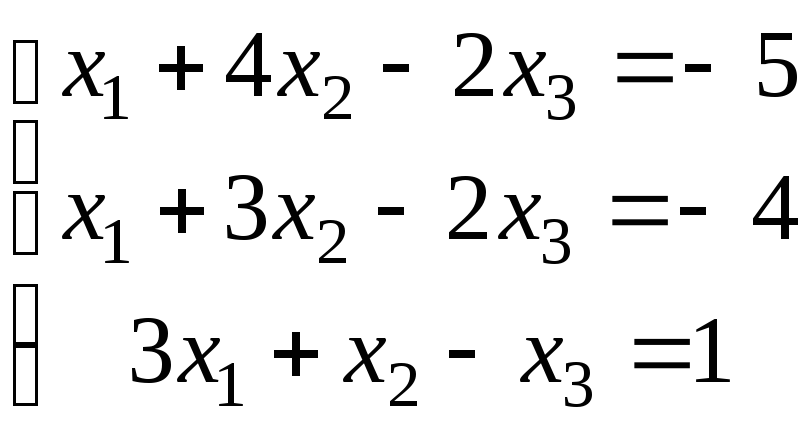 ;
б)
;
б)
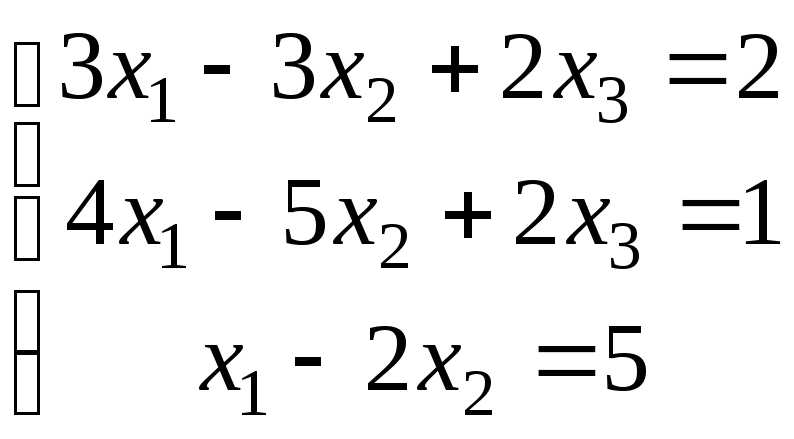 .
.
4.
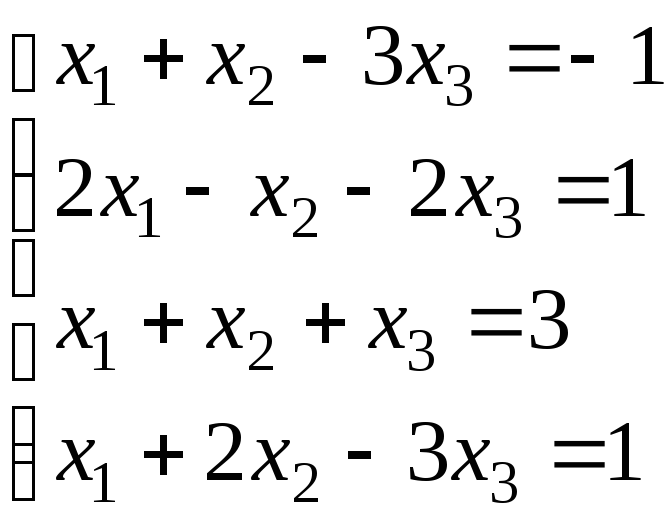 .
5.
.
5.
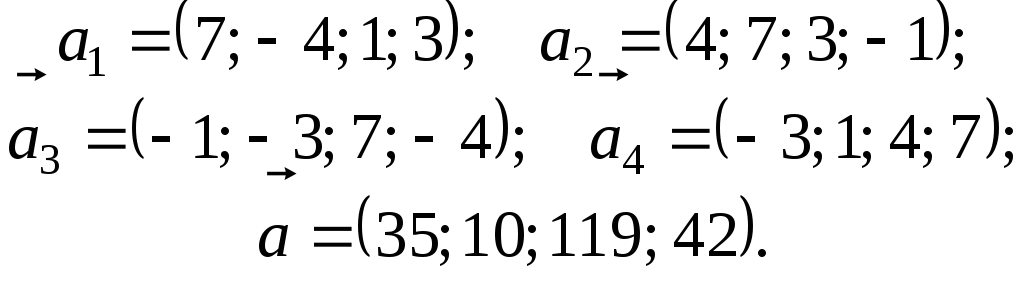
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 5
1.
 ;
;
 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
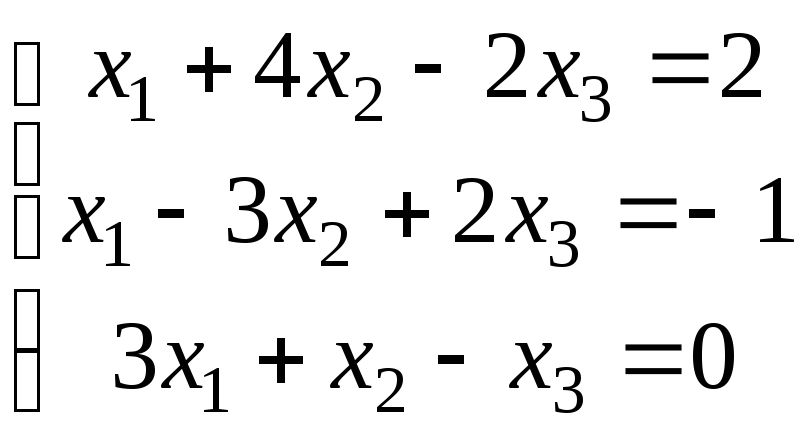 ;
б)
;
б)
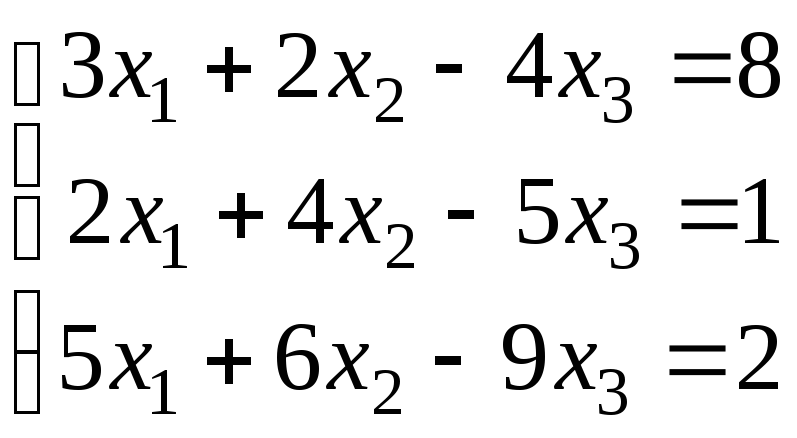 .
.
4.
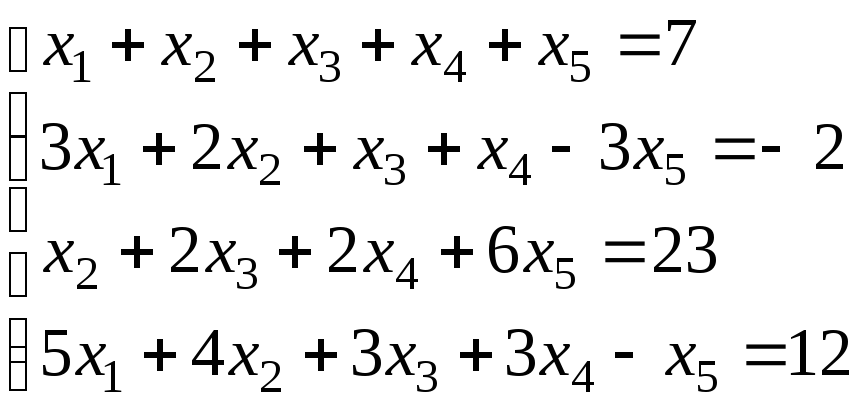 .
5.
.
5.
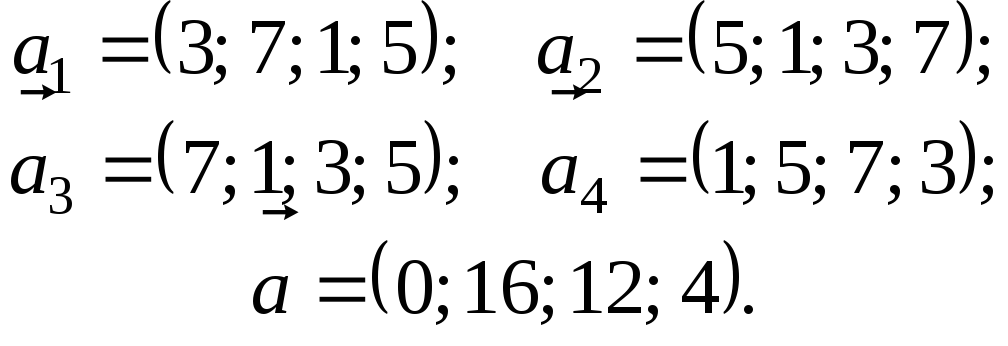
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 6
1.
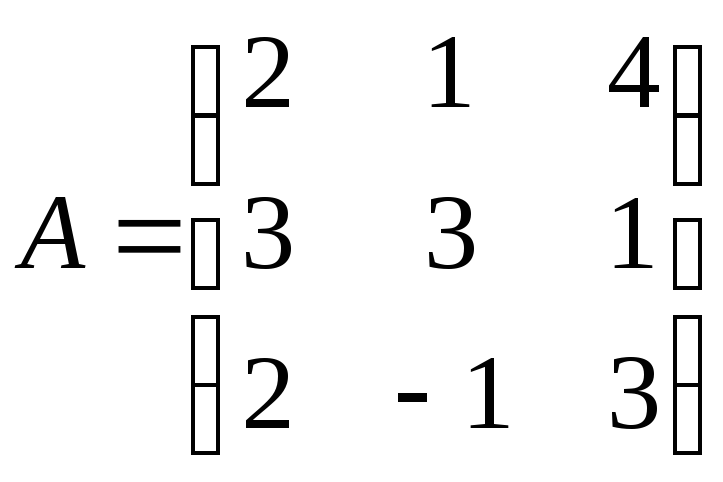 ;
;
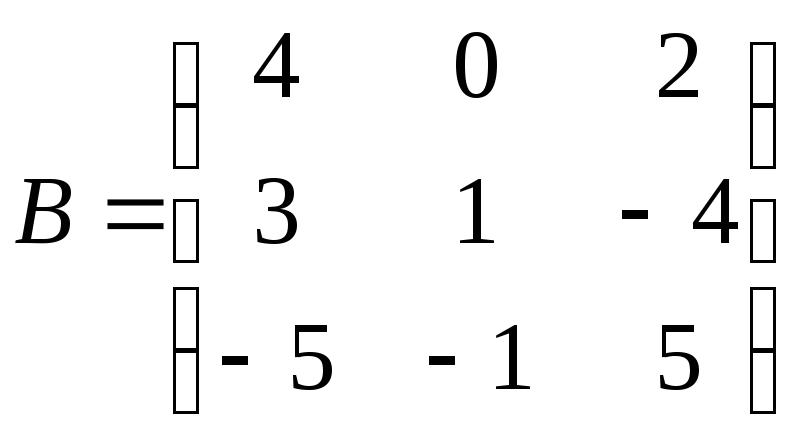 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
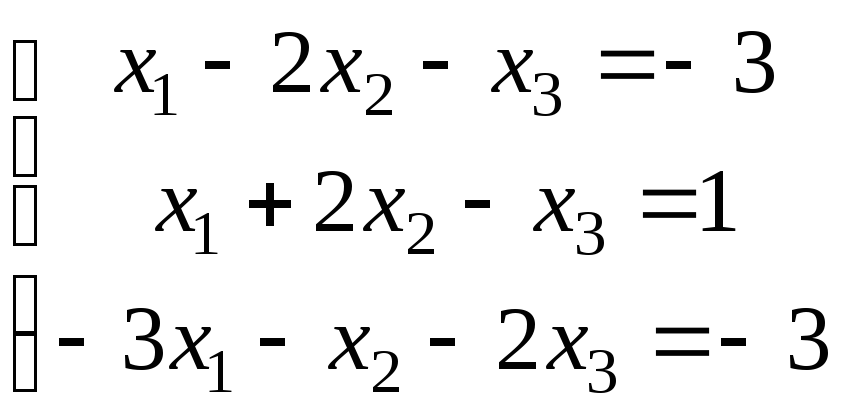 ;
б)
;
б)
 .
.
4.
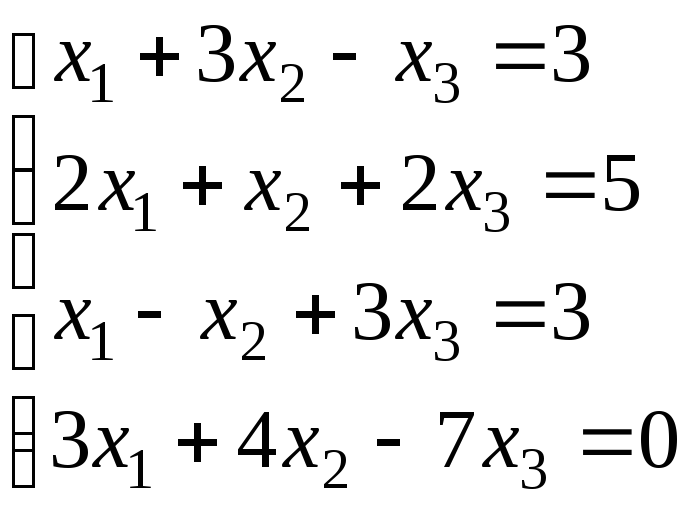 .
5.
.
5.
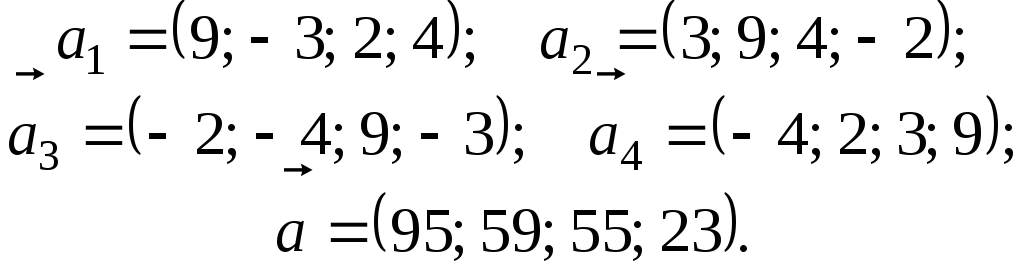
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 7
1.
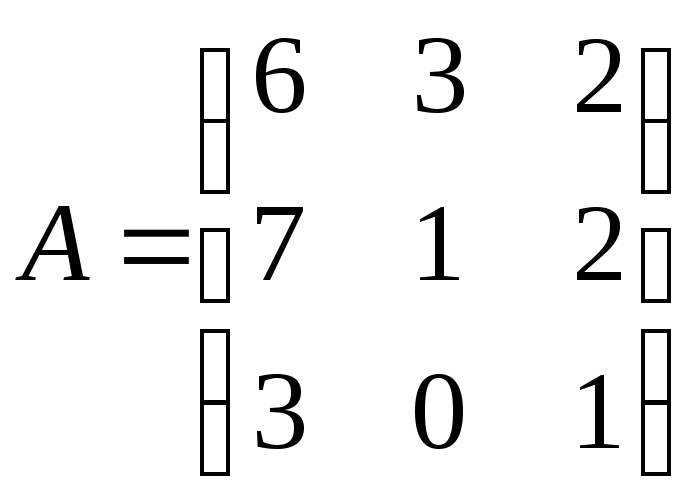 ;
;
 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
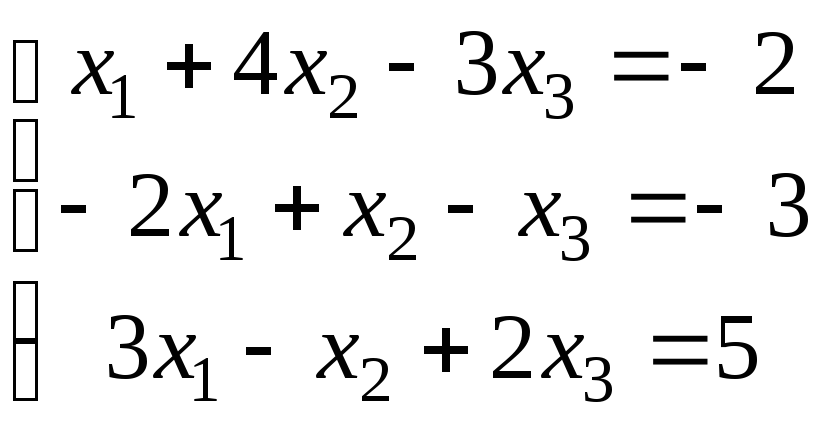 ;
б)
;
б)
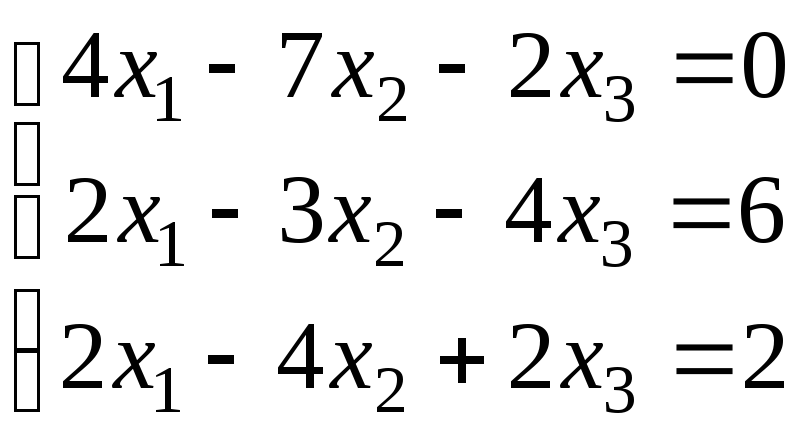 .
.
4.
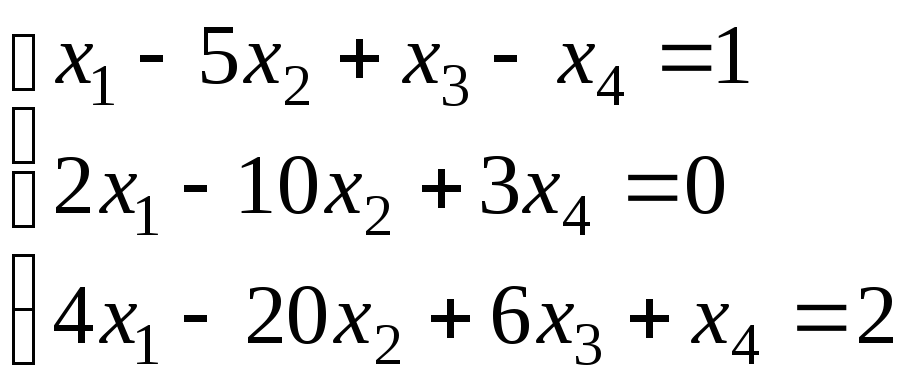 . 5.
. 5.
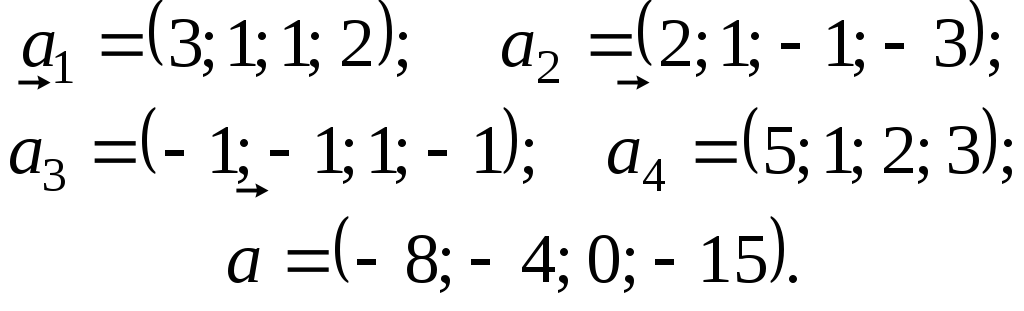
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 8
1.
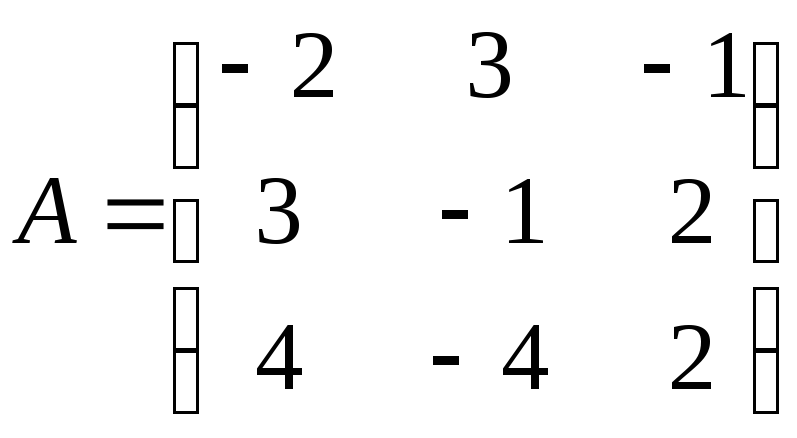 ;
;
 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
 ;
б)
;
б)
 .
.
4.
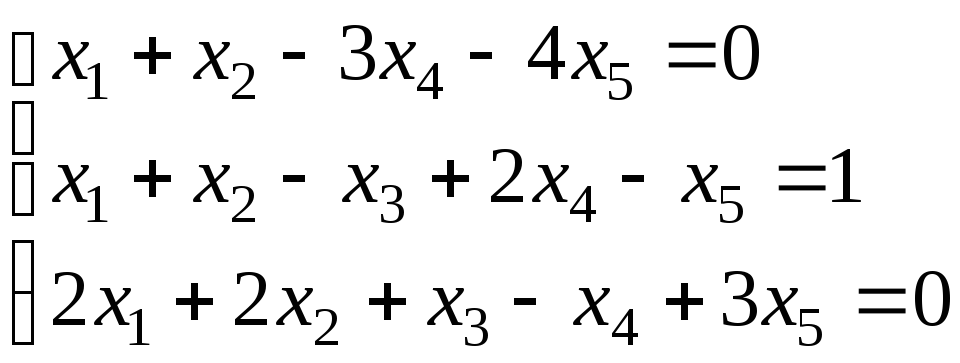 .
.
5.
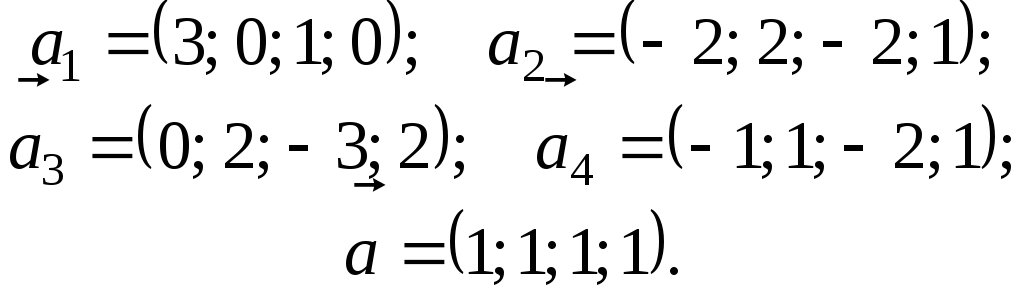 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 9
1.
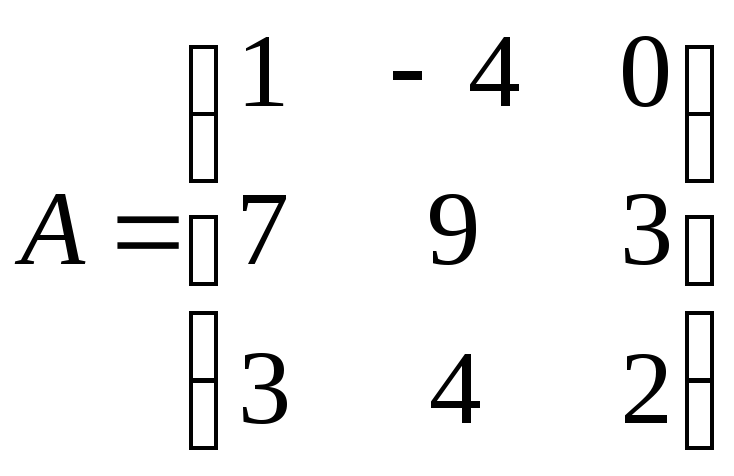 ;
;
 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
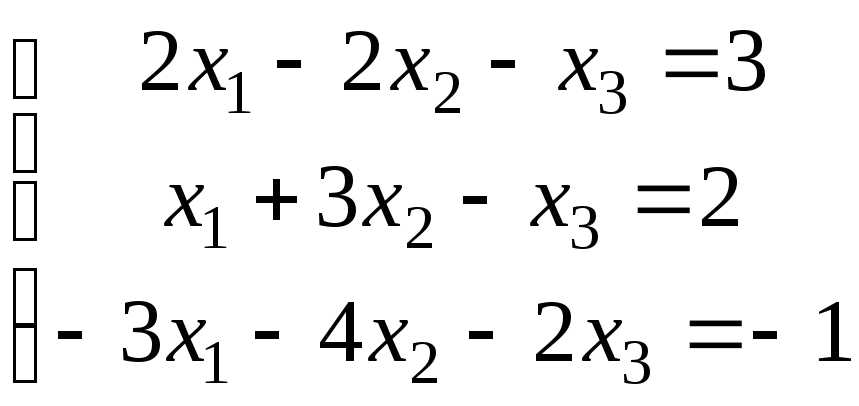 ;
б)
;
б)
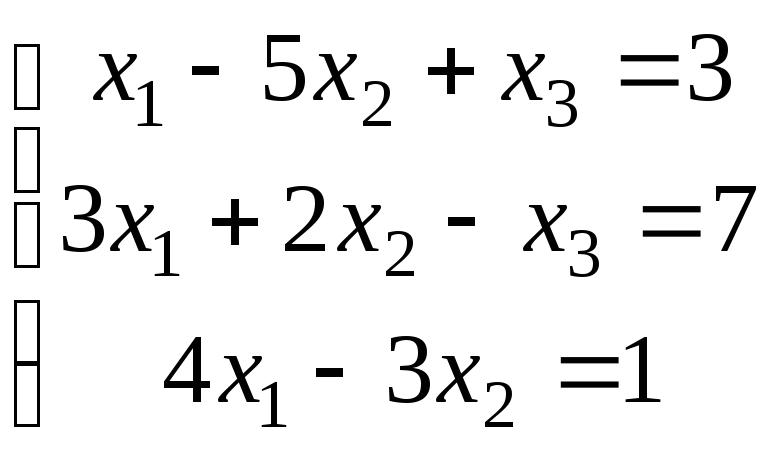 .
.
4.
 .
5.
.
5.
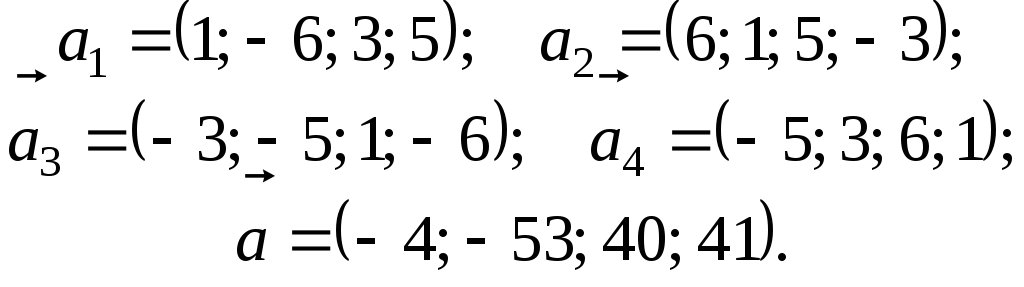
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 10
1.
 ;
;
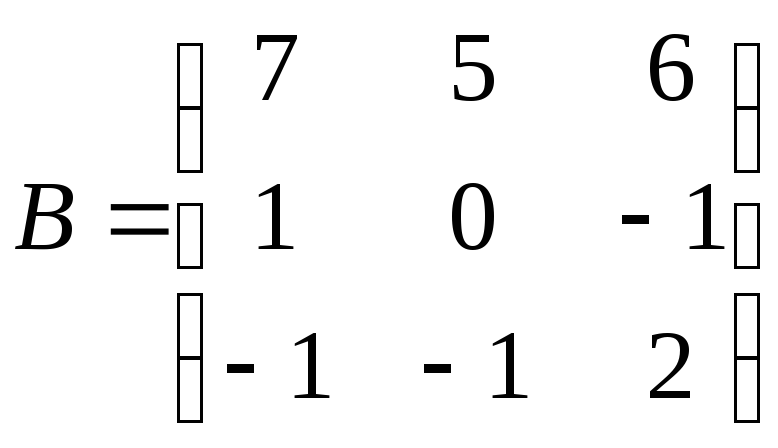 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
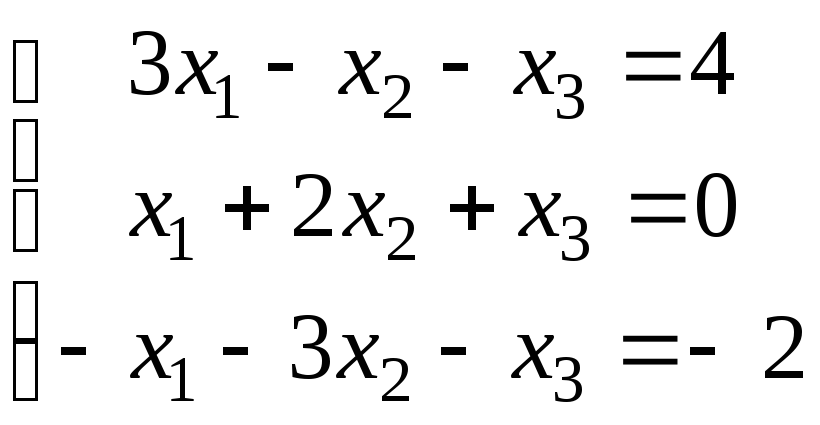 ;
б)
;
б)
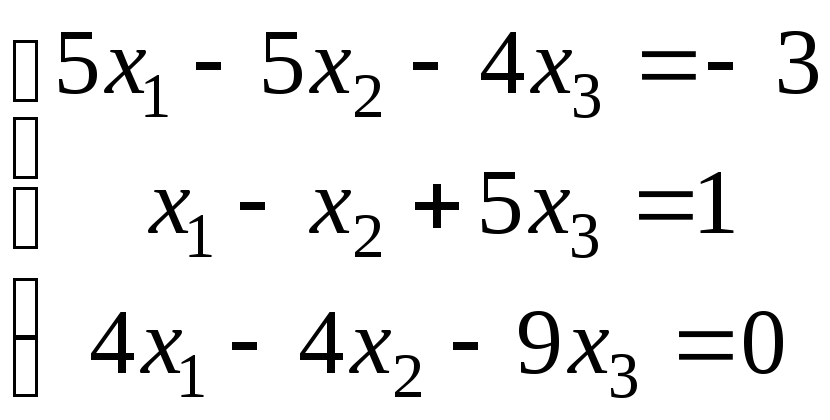 .
.
4.
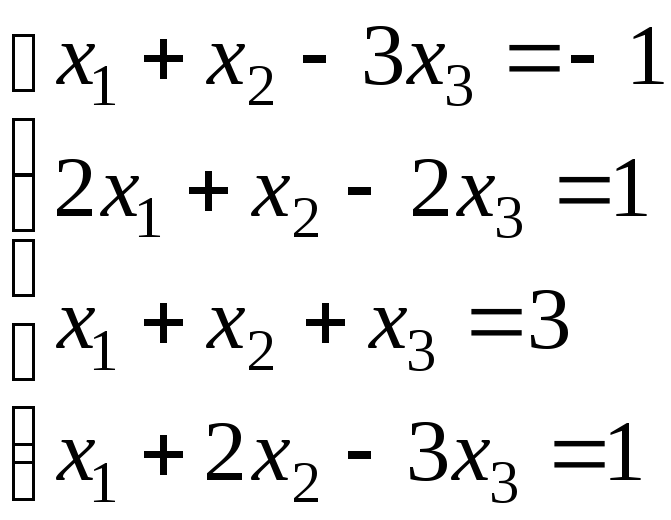 .
5.
.
5.
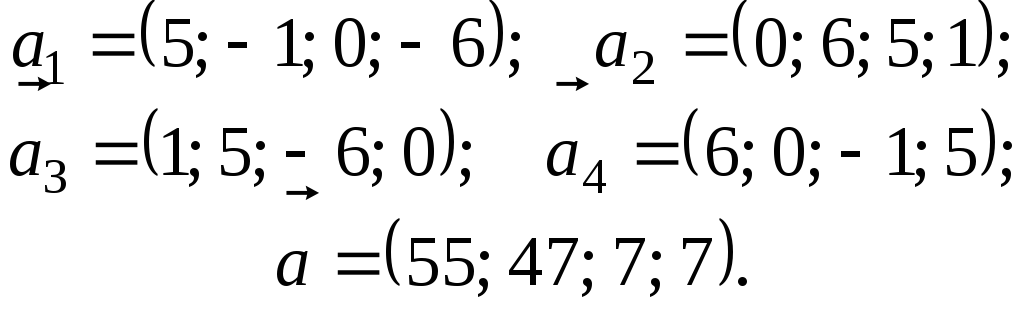
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 11
1.
 ;
;
 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
 ;
б)
;
б)
 .
.
4.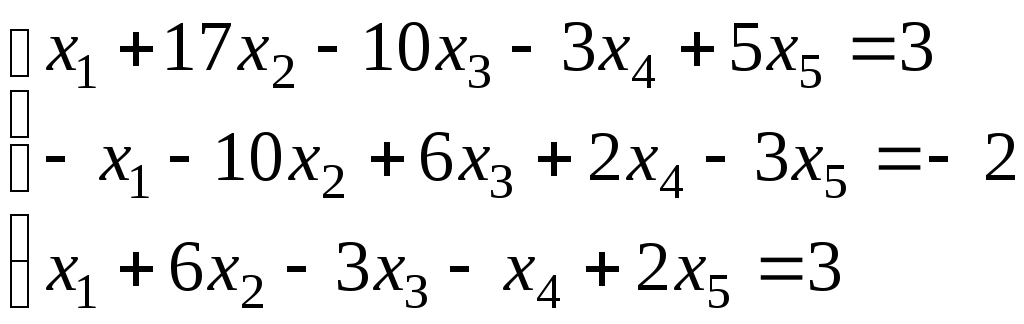 .
.
5.
 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 12
1.
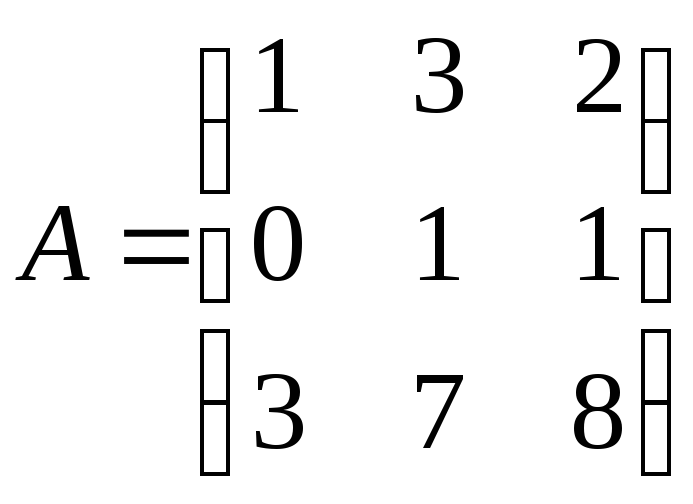 ;
;
 . 2.
. 2.
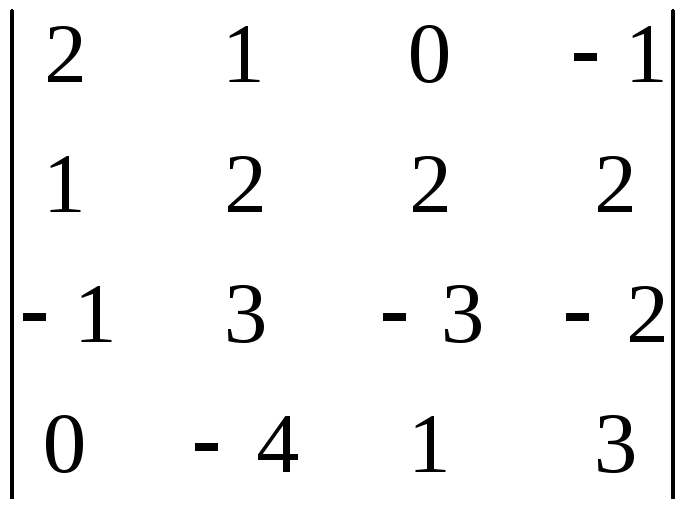 ;
;
![]() .
.
3.
а)
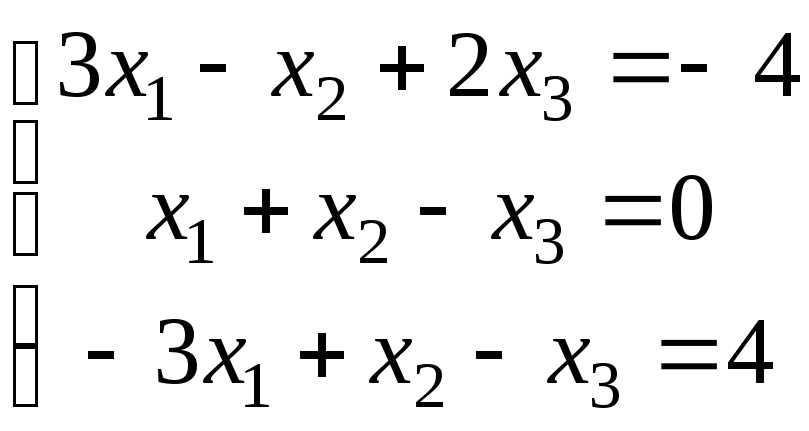 ;
б)
;
б)
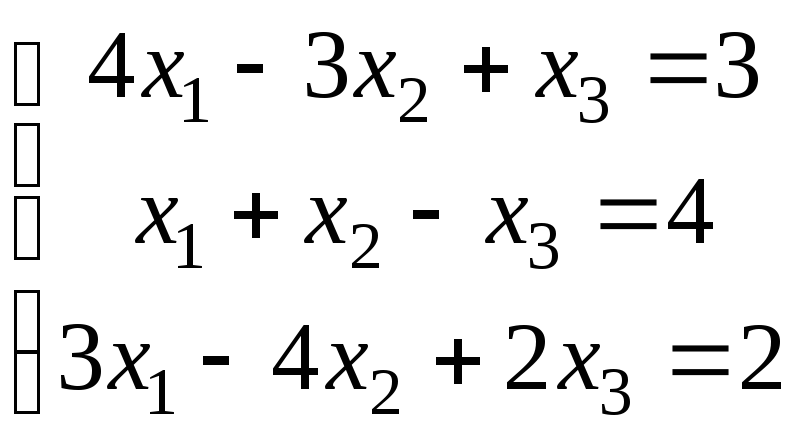 .
.
4.
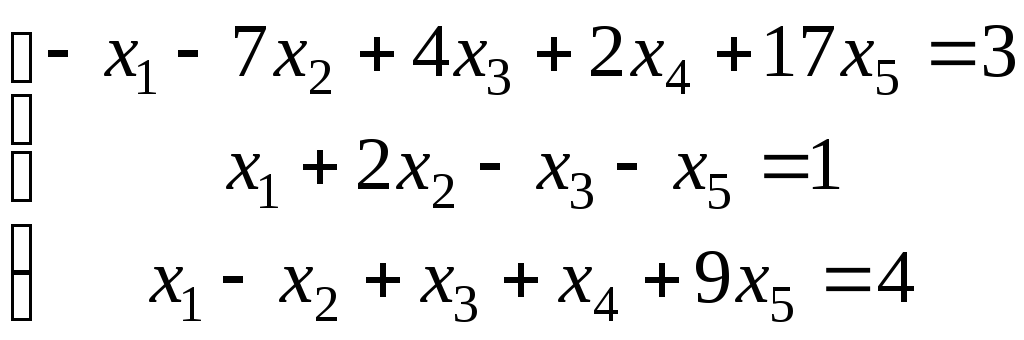 .
.
5.
 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 13
1.
 ;
;
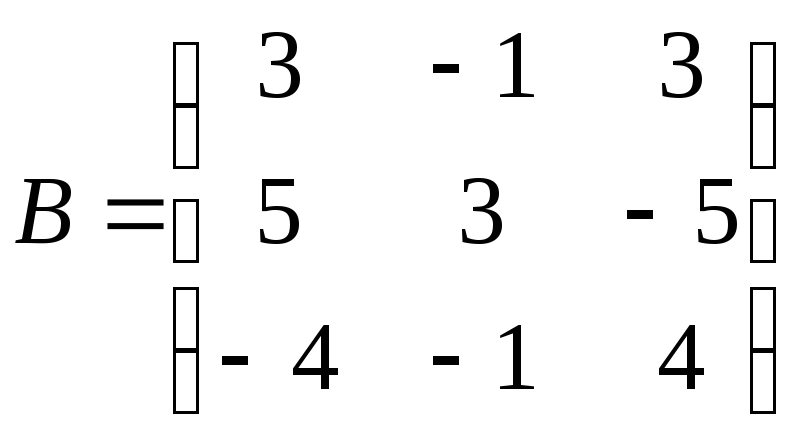 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
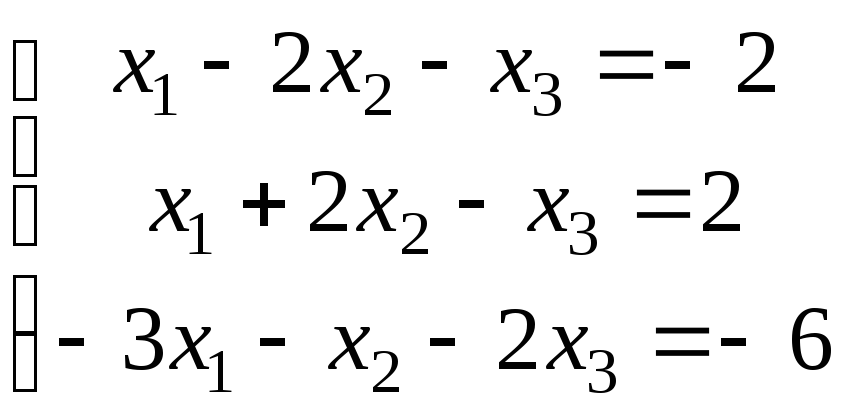 ;
б)
;
б)
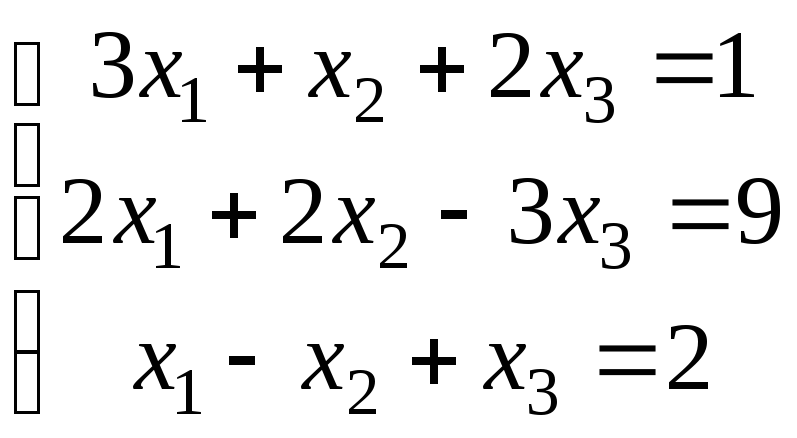 .
.
4.
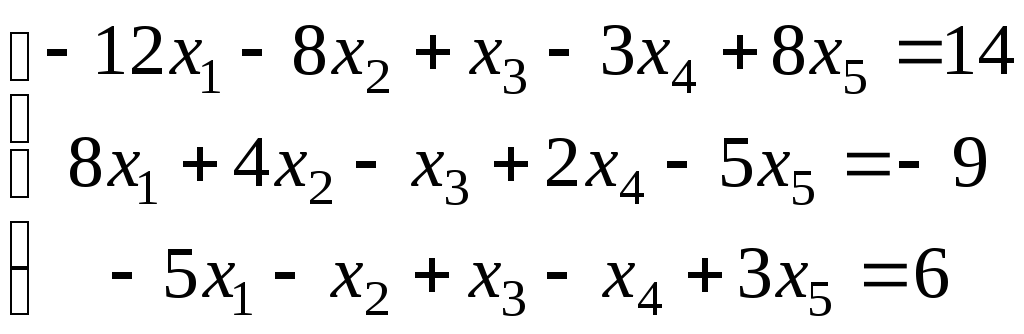 .
.
5.
 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 14
1.
 ;
;
 . 2.
. 2.
 ;
;
![]() .
.
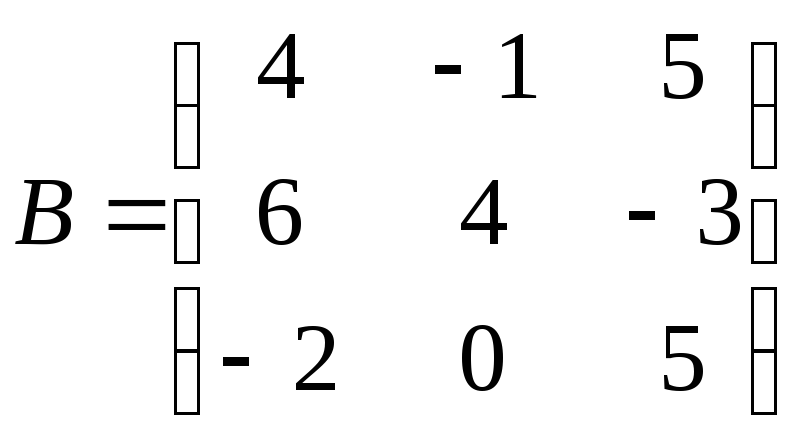
3.
а)
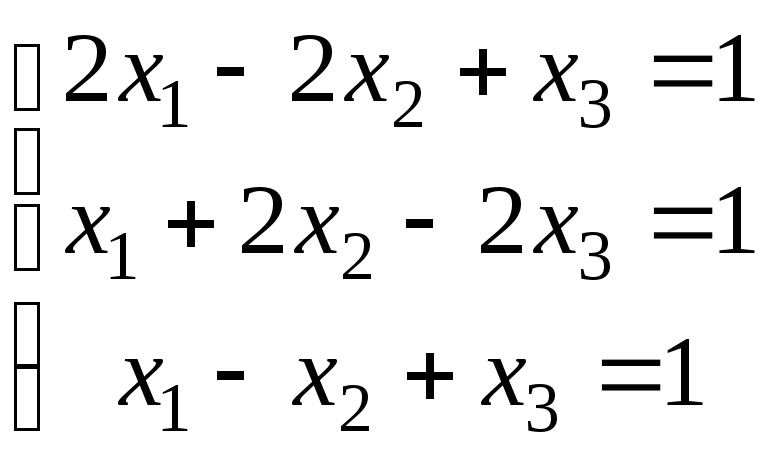 ;
б)
;
б)
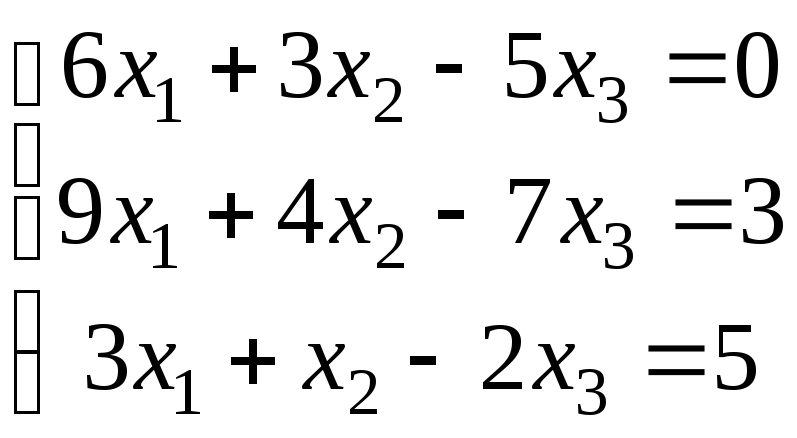 .
.
4.
 .
.
5.
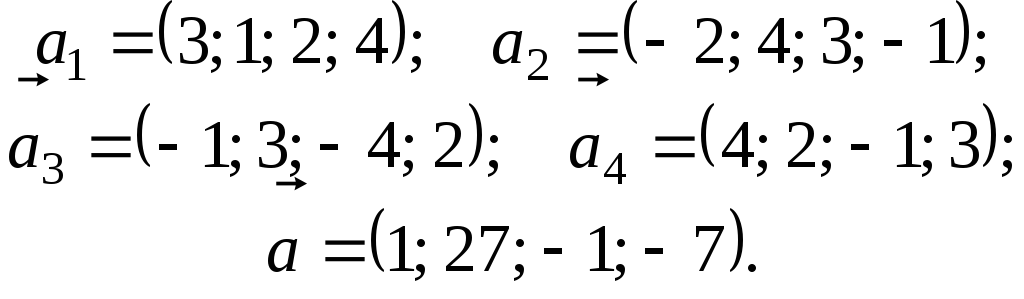 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 15
1.
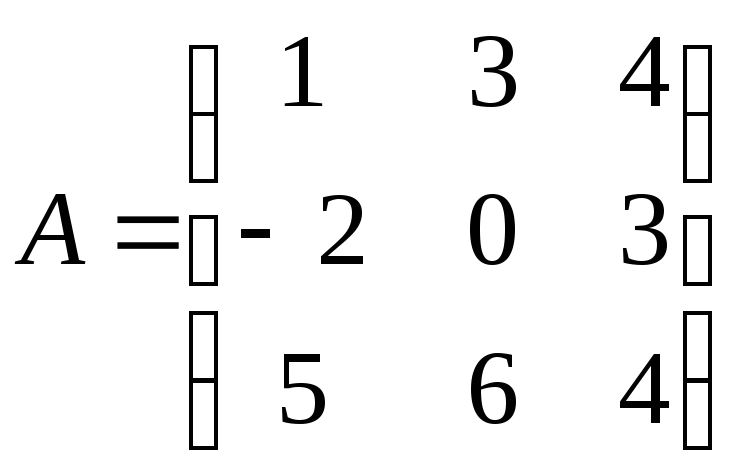 ;
;
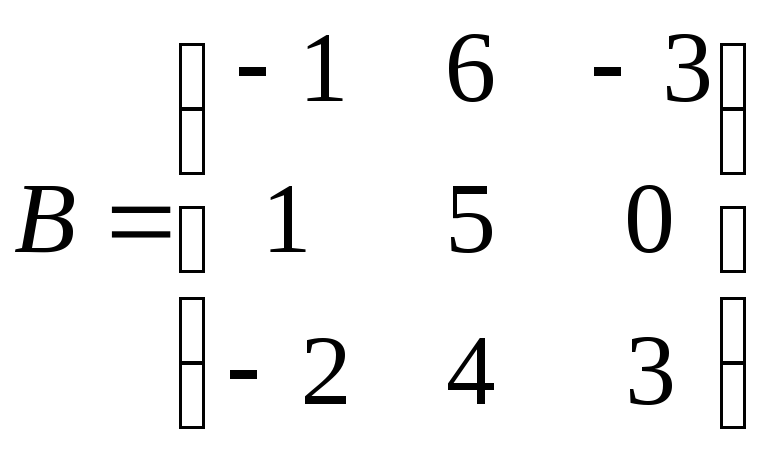 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
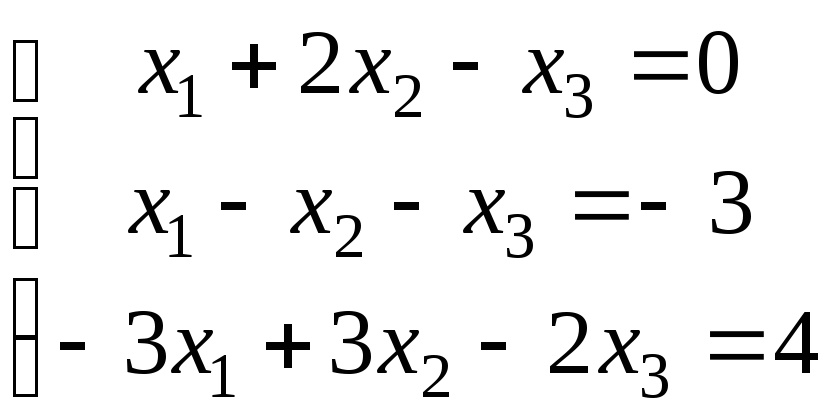 ;
б)
;
б)
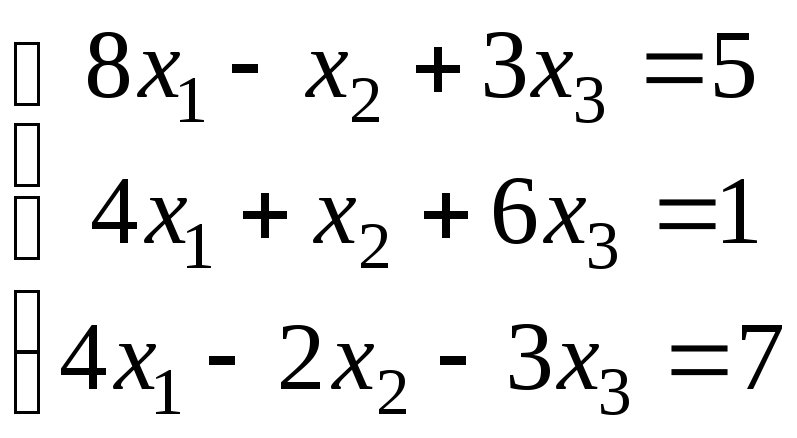 .
.
4.
 .
.
5.
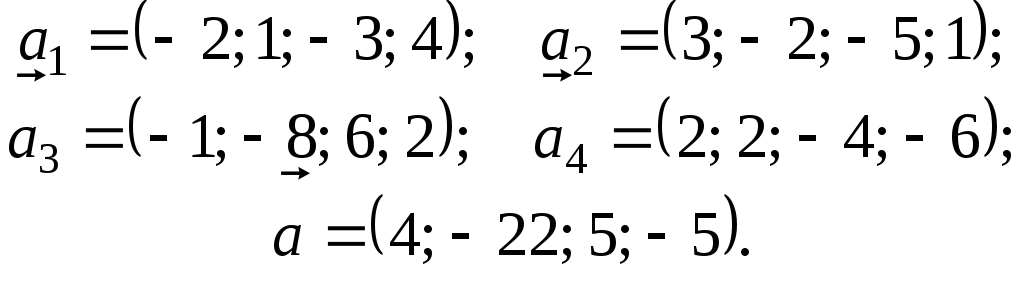 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 16
1.
 ;
;
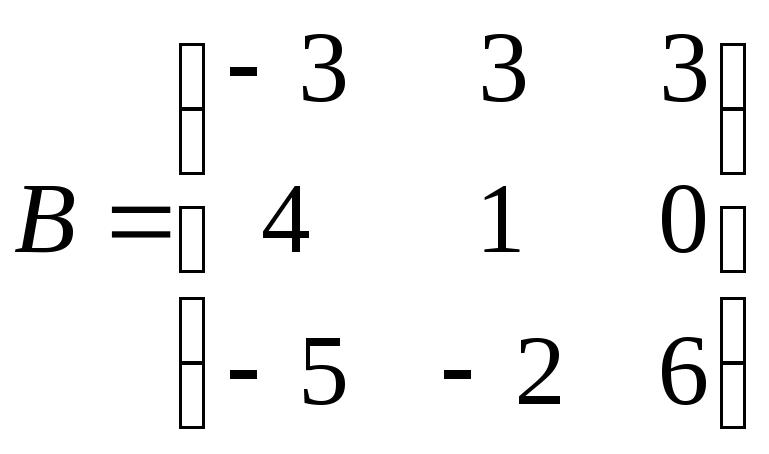 . 2.
. 2.
 ;
; ![]() .
.
3.
а)
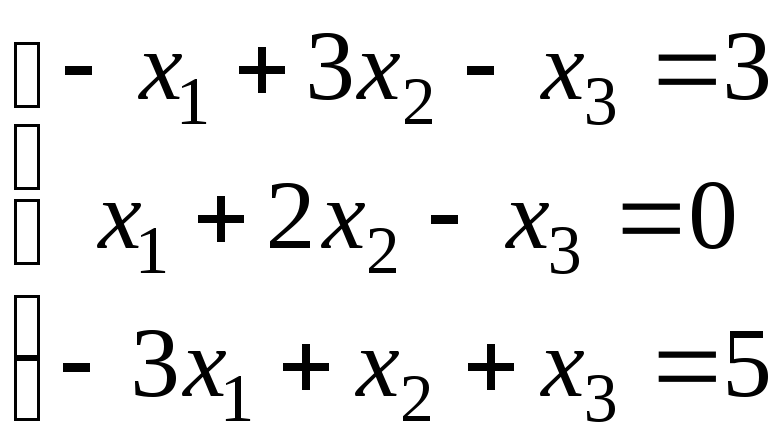 ;
б)
;
б)
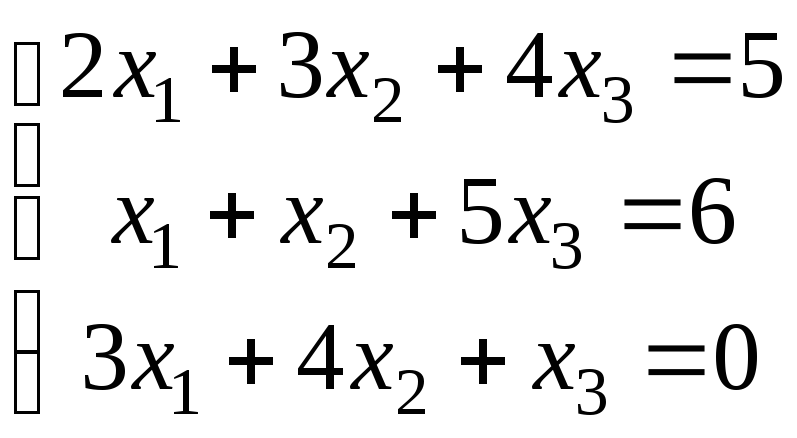 .
.
4.
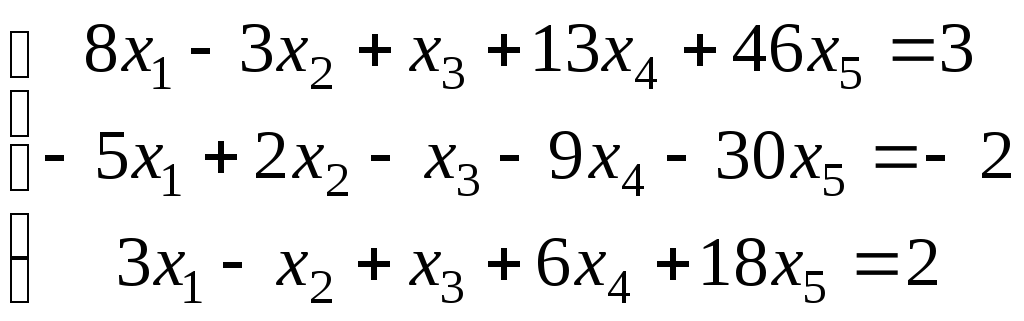 .
.
5.
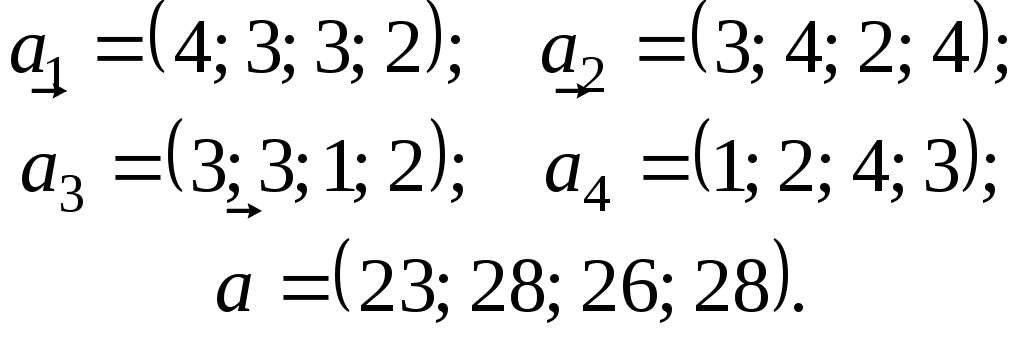 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 17
1.
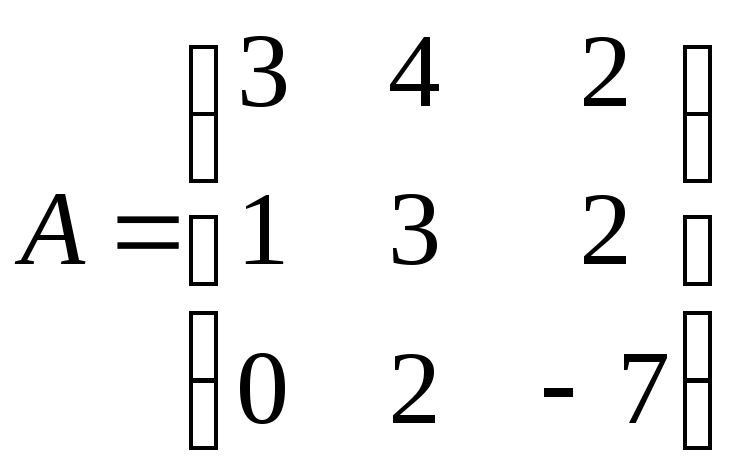 ;
;
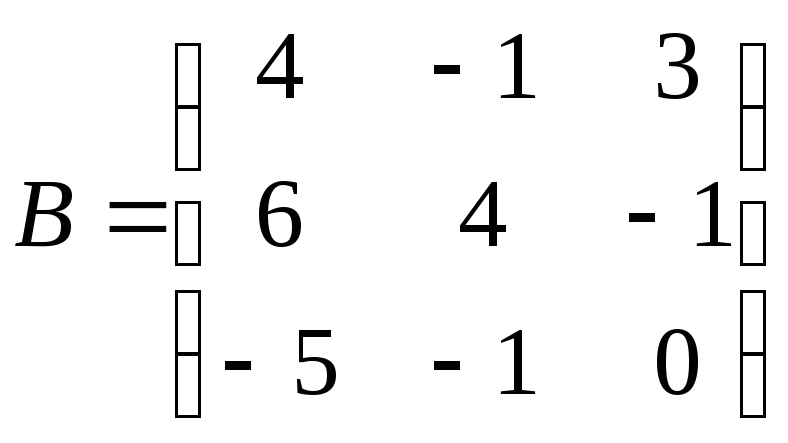 . 2.
. 2.
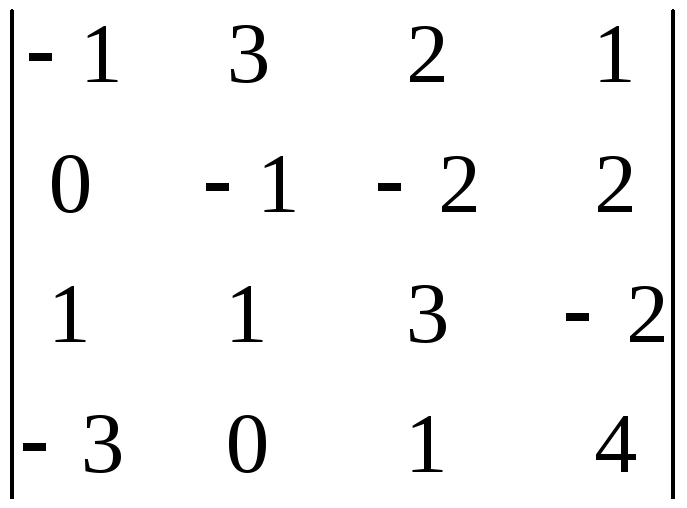 ;
;
![]() .
.
3.
а)
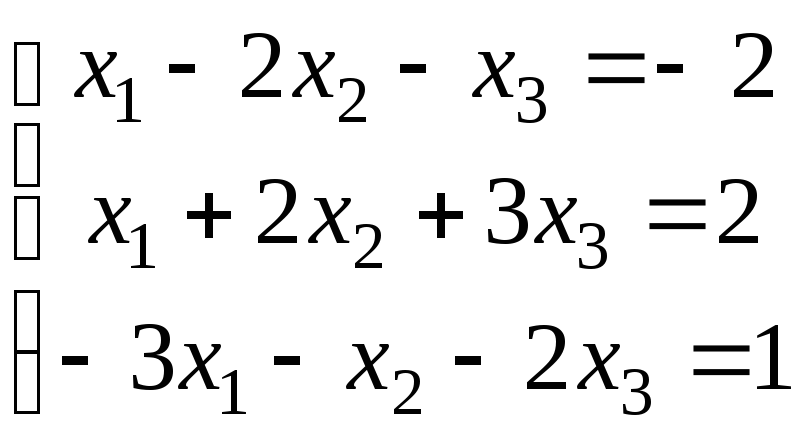 ;
б)
;
б)
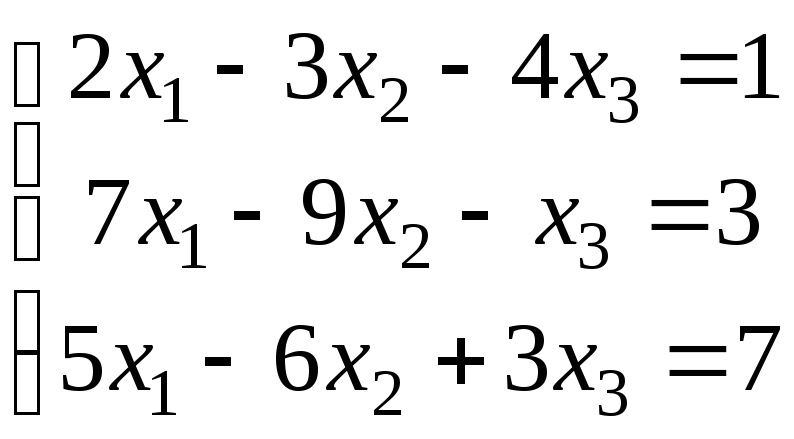 .
.
4.
 .
.
5.
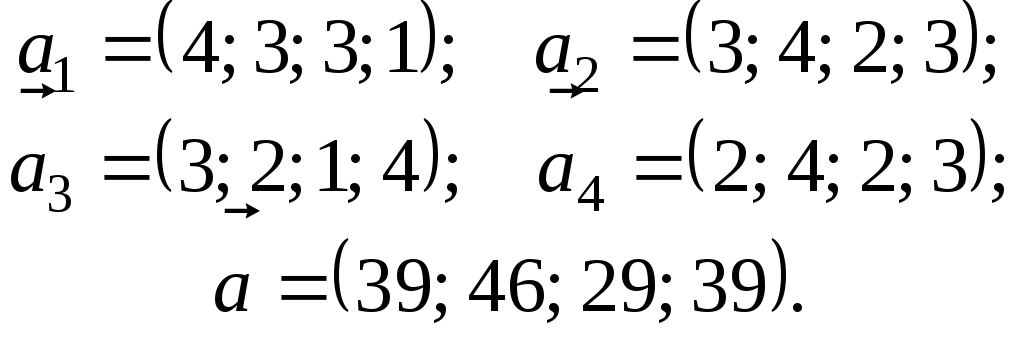 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 18
1.
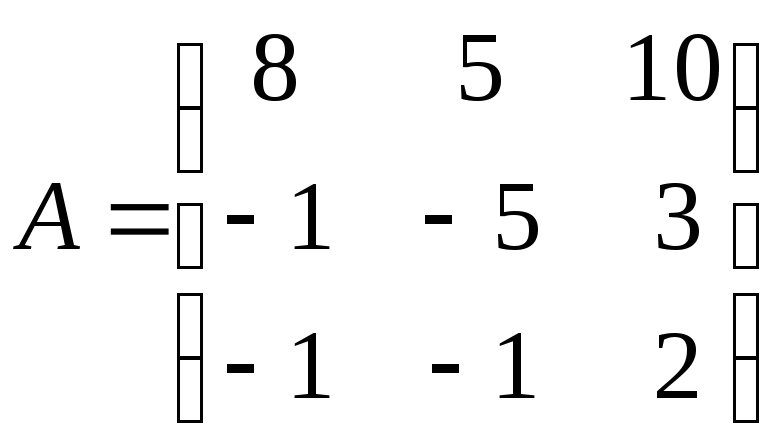 ;
;
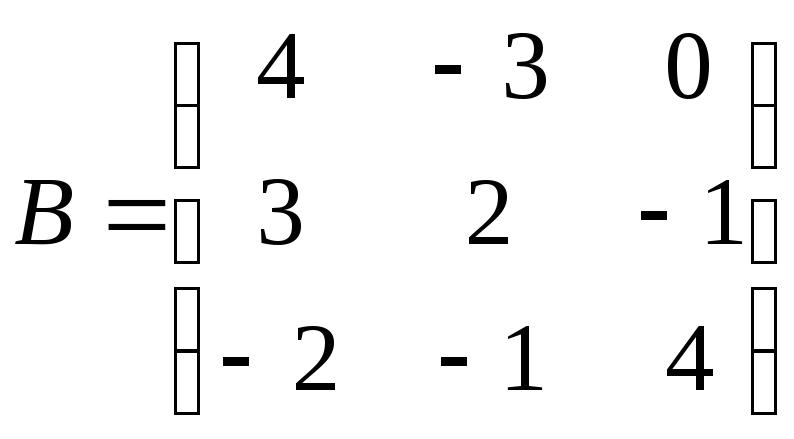 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
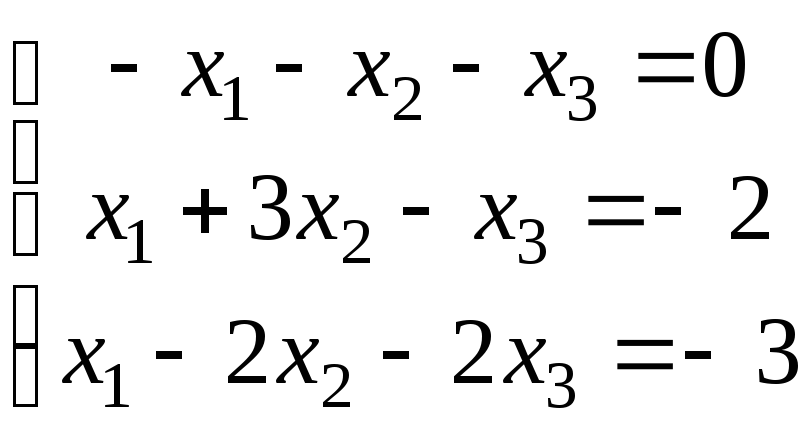 ;
б)
;
б)
 .
.
4.
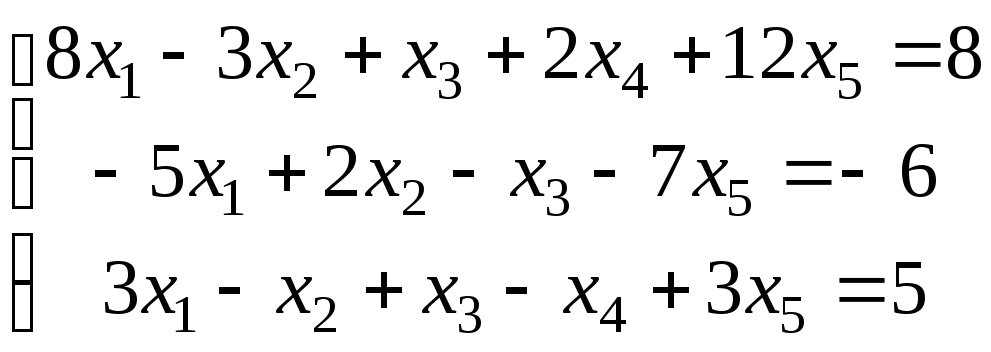 .
.
5.

6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 19
1.
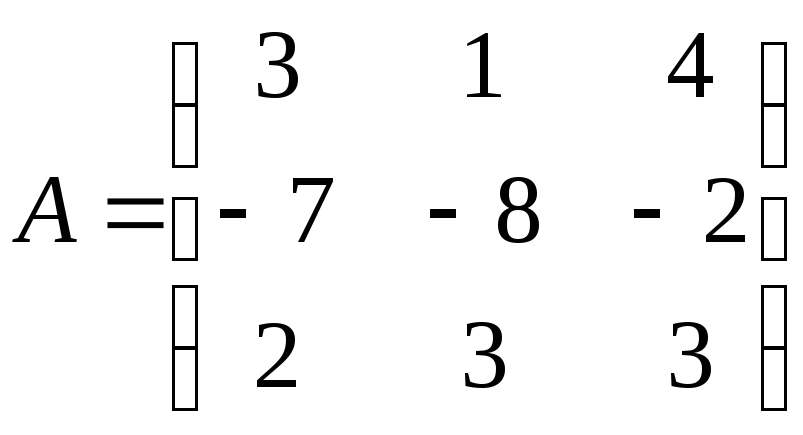 ;
;
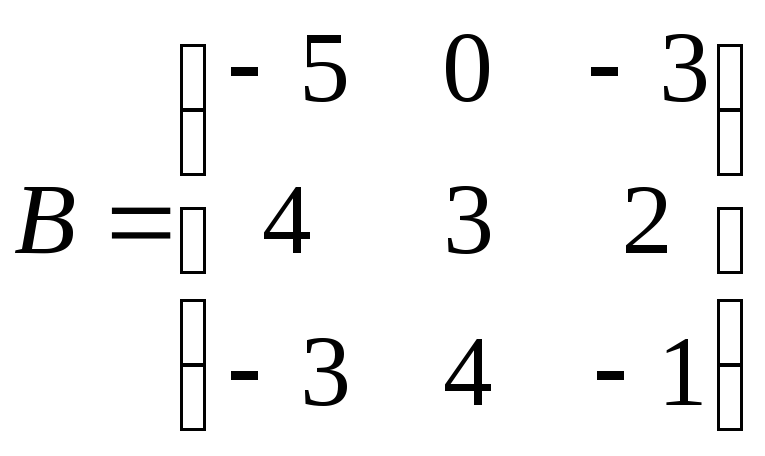 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
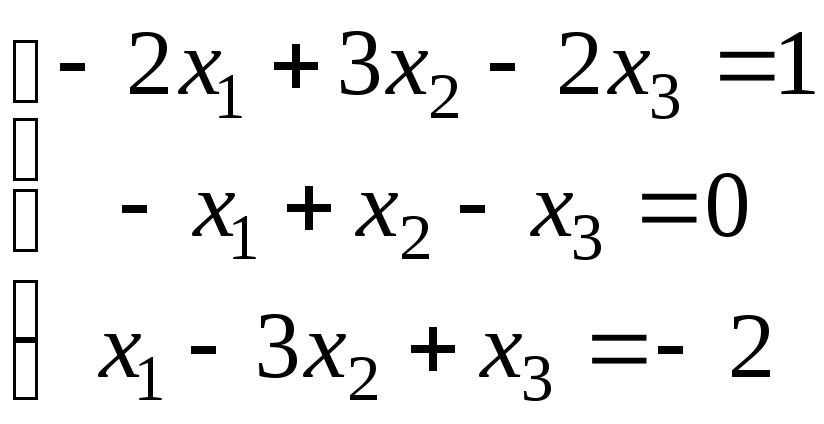 ;
б)
;
б)
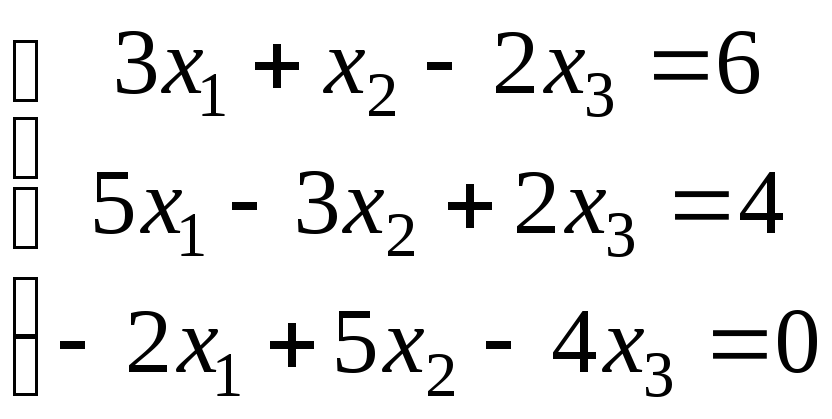 .
.
4.
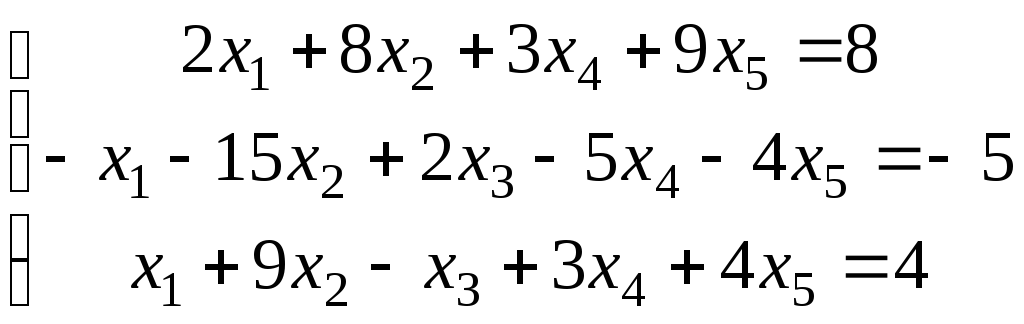 .
.
5.
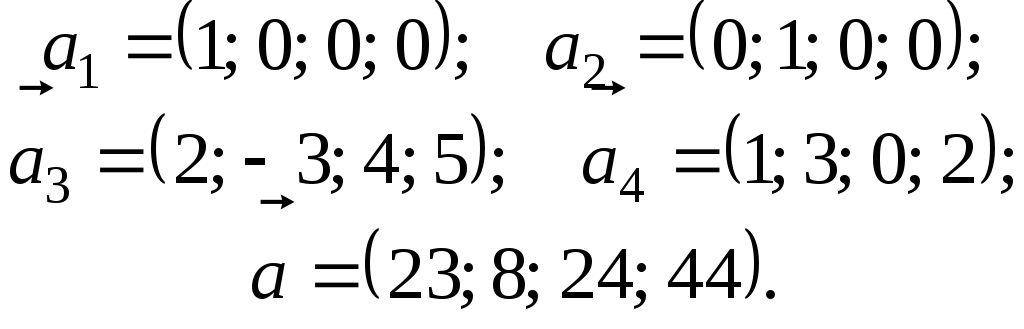 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 20
1.
 ;
;
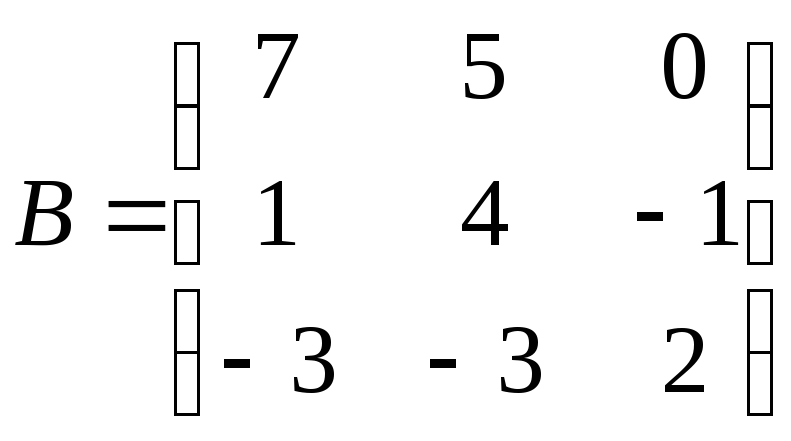 . 2.
. 2.
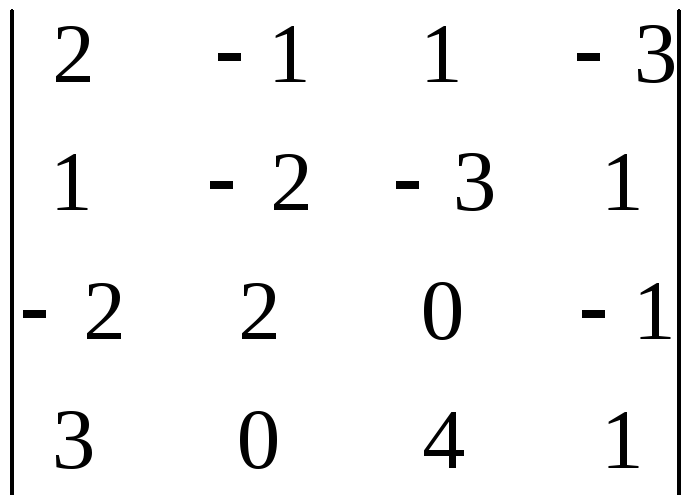 ;
;
![]() .
.
3.
а)
 ;
б)
;
б)
 .
.
4.
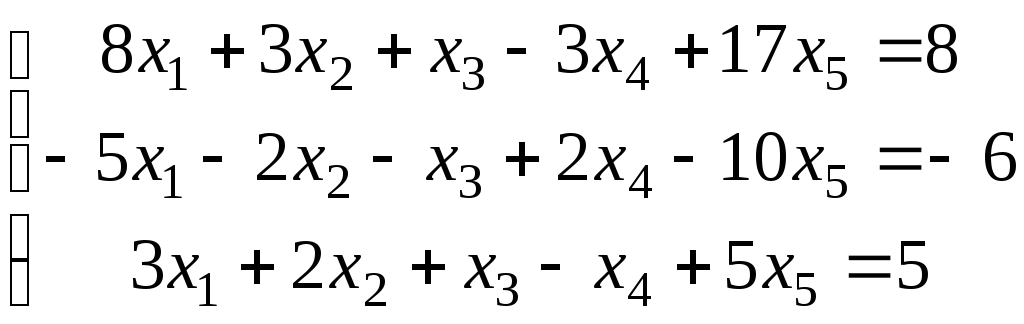 .
.
5.
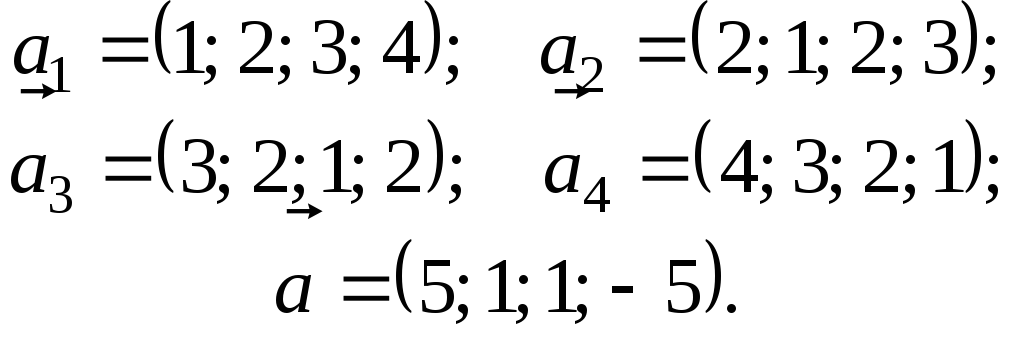 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 21
1.
 ;
;
 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
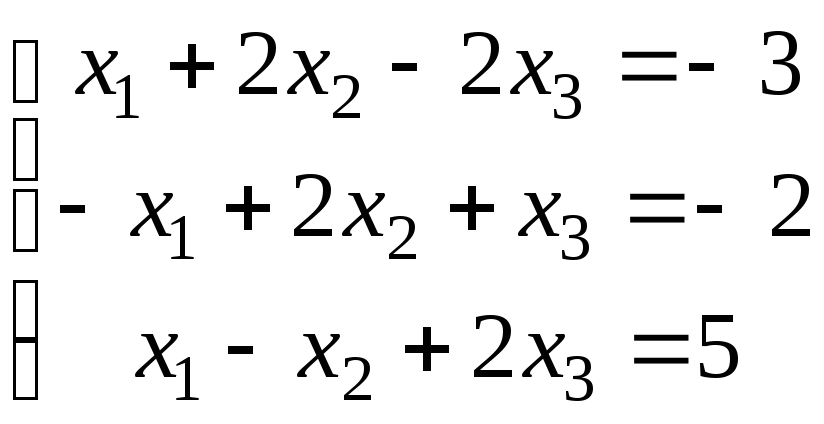 ;
б)
;
б)
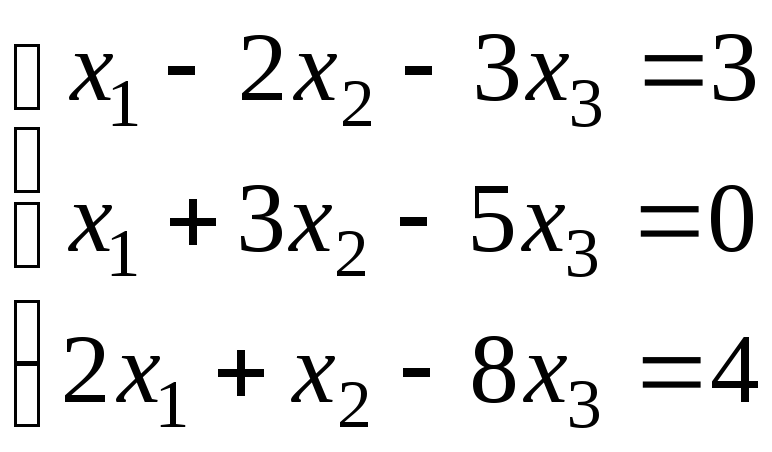 .
.
4.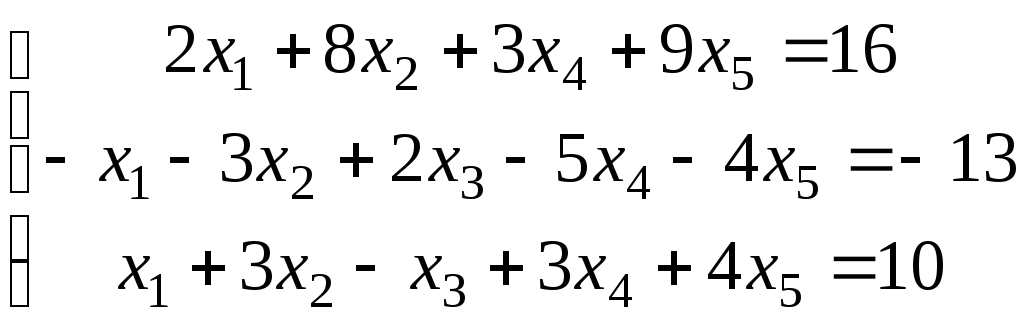 .
.
5.
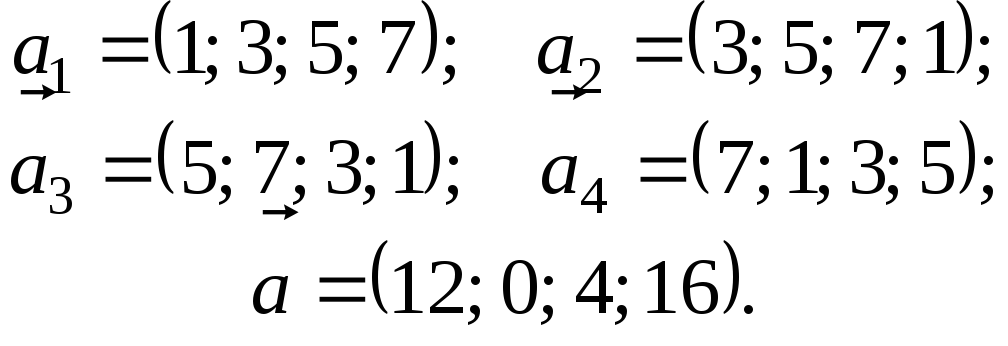 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 22
1.
 ;
;
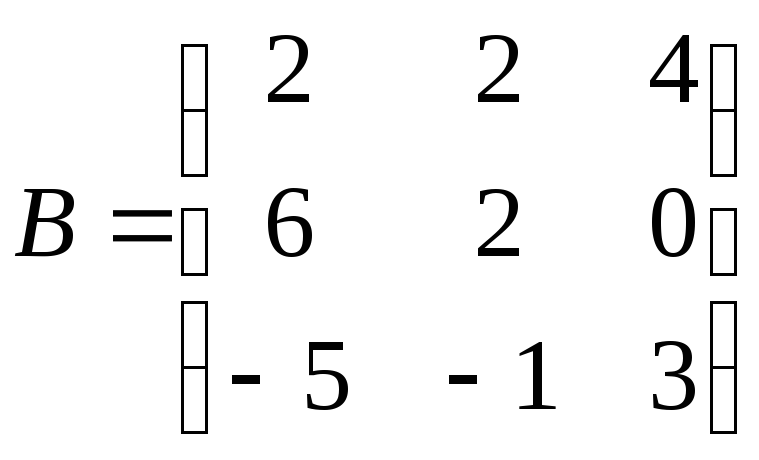 . 2.
. 2.
 ;
;
![]() .
.
3.
а)
 ;
б)
;
б)
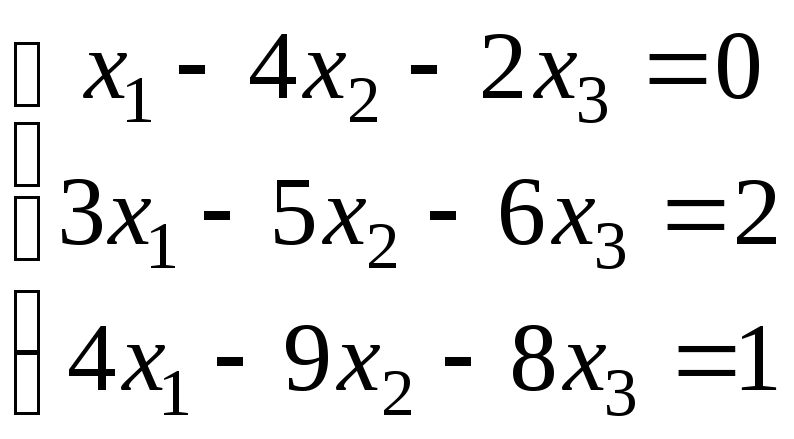 .
.
4.
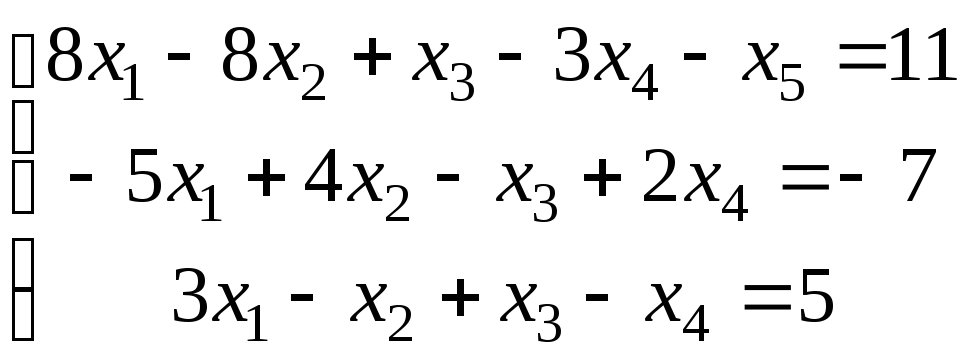 .
.
5.
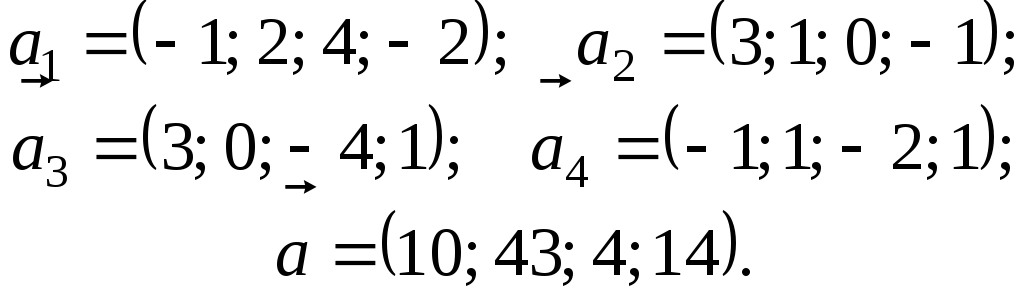 6.
6.
![]() .
.
7.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Варіант 23
1.
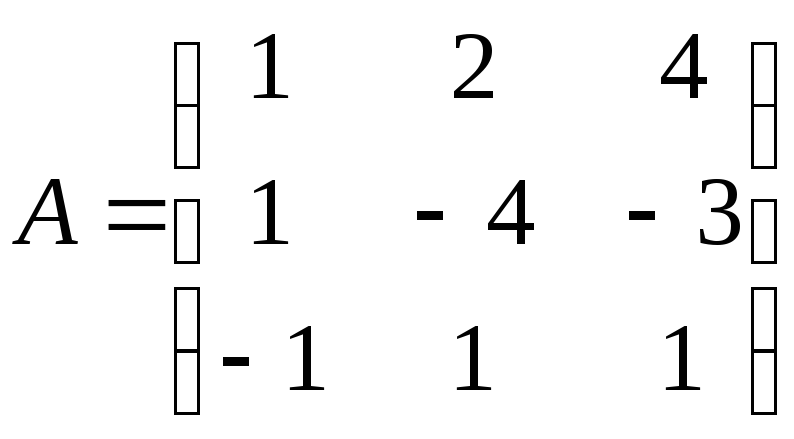 ;
;
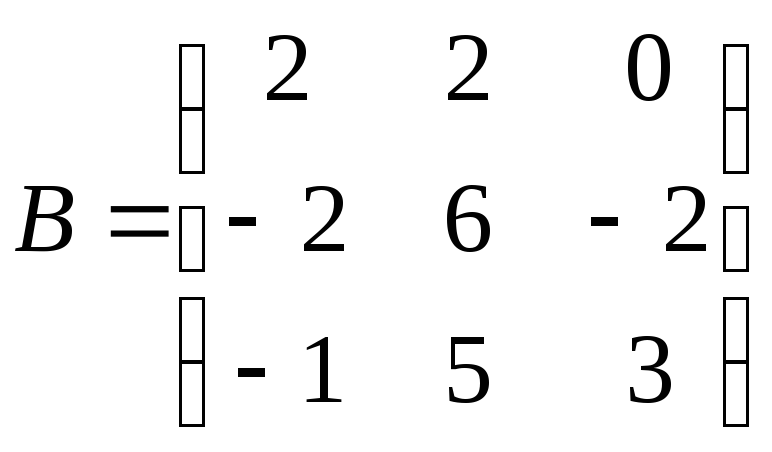 . 2.
. 2.
 ;
;
