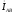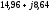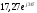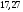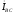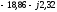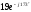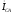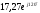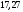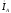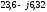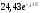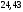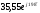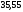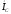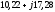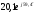- •1.2. Методика расчета линейных электрических цепей постоянного тока
- •2.2. Методика расчета однофазных линейных электрических цепей переменного токи
- •3.2. Методика расчета трехфазных электрических цепей переменного тока
- •3.2.1. Методика расчета трехфазных электрических цепей переменного тока при соединении потребителей звездой
- •3.2.2. Методика расчета трехфазных электрических цепей переменного тока при соединении треугольником
3.2. Методика расчета трехфазных электрических цепей переменного тока
3.2.1. Методика расчета трехфазных электрических цепей переменного тока при соединении потребителей звездой
В цепи, изображенной на схеме (рис. 3.1), потребители трехфазного тока соединены звездой.
Известно
линейное напряжение
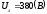 и сопротивления фаз:
и сопротивления фаз:
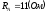 ,
,
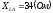 ,
,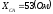 ,
,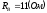 ,
,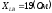 ,
,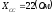 .
.
Определить
полные сопротивления фаз, фазные токи
и ток в нейтральном проводе, активную,
реактивную и полную мощности каждой
фазы и всей цепи.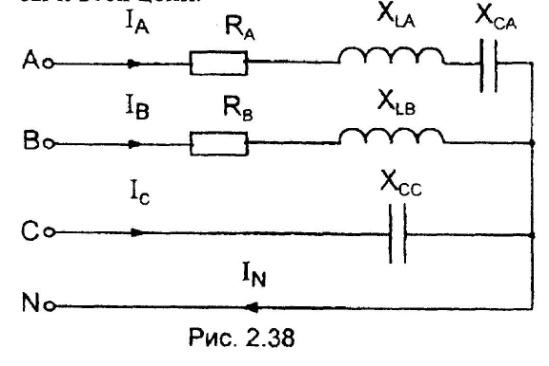
Дано:
 ,
,
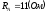 ,
,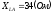 ,
, ,
,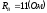 ,
,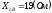 ,
,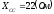 .
.
Определить:

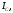
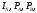
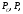
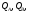
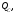
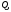
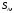
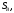
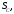
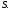
Рис. 3.1
Графоаналитический метод расчета
(расчет с применением векторных диаграмм)
При соединении звездой
 ,
поэтому
,
поэтому

Так
как есть нейтральный провод, то
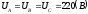
Вычисляем сопротивление фаз и углы φ определяем по диаграммам сопротивлений.

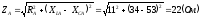 ;
;
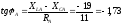 ;
;
 -в
фазе А напряжение отстает от тока на
60°.
-в
фазе А напряжение отстает от тока на
60°.
 ;
;
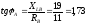 ;
;
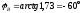 -
в фазе В напряжение опережает ток на
60°
-
в фазе В напряжение опережает ток на
60°
 ;
;
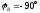 -в
фазе С напряжение отстает от тока на
90°, т. к. в цепь включен конденсатор.
-в
фазе С напряжение отстает от тока на
90°, т. к. в цепь включен конденсатор.
Фазные токи можно определить следующим образом:
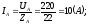
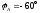 ;
;
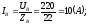
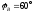 ;
;
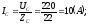
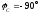 .
.
Чтобы вычислить ток в нейтральном проводе, нужно построить векторную диаграмму цепи.
На векторной диаграмме под углом 120° друг относительно друга строятся векторы фазных напряжений одинаковой длины.
Векторы
фазных токов строятся в масштабе под
вычисленными углами φ
по отношению к фазным напряжениям. В
фазе А
нагрузка носит емкостный характер,
значит, ток
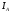 опережает напряжение
опережает напряжение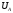 на
угол
на
угол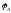 .
.
В
фазе В
нагрузка носит индуктивный характер,
следовательно, ток
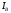 отстает от напряжения
отстает от напряжения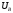 нa
угол
нa
угол
 .
.
В
фазе С
нагрузка емкостная, следовательно, ток
 опережает напряжение
опережает напряжение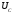 на угол
на угол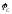 .
.
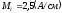 -
масштаб.
-
масштаб.
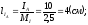
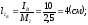
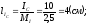
Ток в нейтральном проводе равен геометрической (векторной) сумме фазных токов: Рис. 3.2
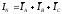
Измерив
длину вектора
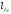 ,
находим
ток
,
находим
ток
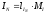
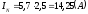
Определим активные мощности фаз:
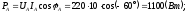

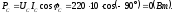
Активная мощность трехфазной цепи:
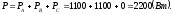
Определяем реактивные мощности фаз:
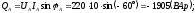
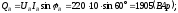

Реактивная мощность трехфазной цепи:

Вычисляем полную мощность каждой фазы и всей цепи:

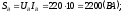
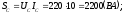
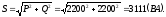
Символический метод расчета
Строгий аналитический расчет трехфазных цепей производится символическим методом, т. е. в комплексной форме.
Выразим в комплексной форме фазные напряжения:

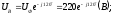

Выразим сопротивления фаз в комплексной форме:
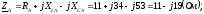
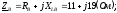
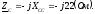
Переведем комплексные сопротивления фаз из алгебраической формы в показательную:
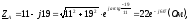
где
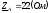 - полное сопротивление фазыА;
- полное сопротивление фазыА;
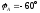 -
угол сдвига фаз между током и напряжением
в фазе А.
-
угол сдвига фаз между током и напряжением
в фазе А.
Аналогично определяем:
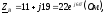
где
 ,
, .
.

где
 ,
,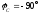 .
.
Находим комплексы фазных токов:

модуль
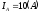 ,
аргумент
,
аргумент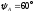 ,
,
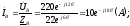
модуль
 ,
аргумент
,
аргумент ,
,
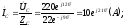
модуль
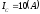 ,
аргумент
,
аргумент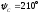 .
.
Находим алгебраическую форму записи комплексов фазных токов:


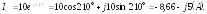
Вычисляем ток в нейтральном проводе:
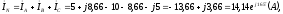
модуль
 ,
аргумент
,
аргумент .
.
Вычисляем мощности фаз и всей цепи:
 где
где
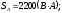
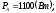

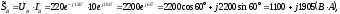 где
где
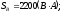

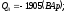
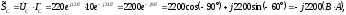 где
где
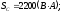

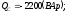
тогда
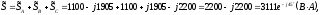
где
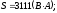
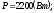

3.2.2. Методика расчета трехфазных электрических цепей переменного тока при соединении треугольником
В
цепи, изображенной на схеме (рис.
3.3),
потребители соединены треугольником.
Известно линейное напряжение
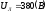 и сопротивления фаз
и сопротивления фаз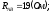
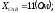


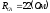 .Определить
фазные, линейные токи, мощности активные,
реактивные, полные мощности каждой фазы
и всей цепи. Построить векторную диаграмму
цепи.
.Определить
фазные, линейные токи, мощности активные,
реактивные, полные мощности каждой фазы
и всей цепи. Построить векторную диаграмму
цепи.

Дано:
 ,
,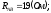
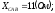
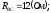

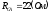 .
.
Определить:
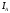 ,
,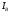 ,
,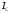 ,
, ,
, ,
,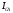 ,
,
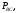
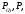
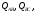
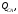
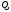
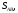


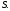
При соединении трехфазной цепи треугольником расчет будем вести
Рис. 3.3 символическим метолом.
Модули фазных напряжений при соединении треугольником равны линейным напряжениям
 ,
то есть
,
то есть
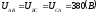 .
.
Комплексы
данных напряжений запишем из условия,
что вектор
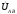 совмещен
с действительной осью комплексной
плоскости
совмещен
с действительной осью комплексной
плоскости


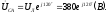
Вычислим комплексы фазных сопротивлений:
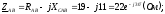
где
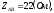


где
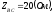
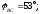

где
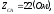
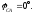
Определяем фазные токи:
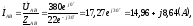
модуль
 ,
,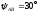 ;
;
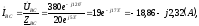
модуль
 ,
,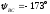 ;
;

модуль
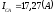 ,
, .
.
Находим линейные токи из уравнений, записанных по первому закону Кирхгофа для узлов В, А, С (рис. 3.3).

модуль
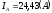 ,
аргумент
,
аргумент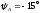 ;
;
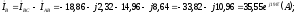
модуль
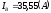 ,
аргумент
,
аргумент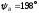 ;
;
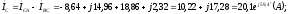
модуль
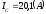 ,
аргумент
,
аргумент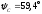 .
.
Вычисляем мощности каждой фазы и всей цепи:
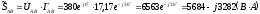 ,
,
где

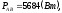
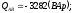
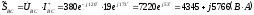 ,
,
где
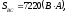
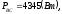
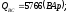
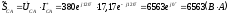 ,
,
где


 где
где
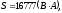


Строим в масштабе векторную диаграмму напряжений и токов.
Векторы
фазных токов
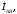
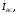
 строятся под углами
строятся под углами
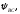
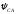 к
действительной оси. К концам векторов
к
действительной оси. К концам векторов
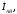
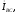
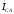 пристраиваются отрицательные фазные
токи согласно уравнениям:
пристраиваются отрицательные фазные
токи согласно уравнениям:
 ;
;
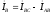 ;
;
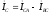 .
.
Замыкающие
векторные треугольники векторов
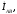
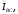
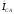 представляют в выбранном масштабе
линейные токи.
представляют в выбранном масштабе
линейные токи.
Выбираем
масштаб:
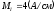
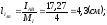
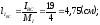
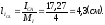
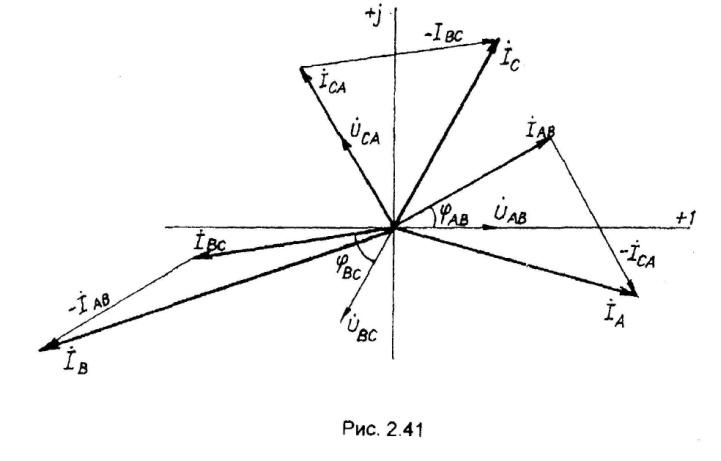
Рис. 3.4
Результаты расчетов занесем в соответствующие таблицы
Результаты расчета токов
|
Фазные и линейные токи |
Алгебраическая форма, А |
Показательная форма, А |
Действующее значение, А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|