
ПРЕДЕЛЫ И ИХ СВОЙСТВА (шпаргалка)
.doc
ПРЕДЕЛЫ И ИХ СВОЙСТВА Составил: |
||
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ И ФУНКЦИИЧисло А наз. пределом Xn при n, где n если для >0 N() > 0, такой, что |Xn - A|< для n>N().
Число
А наз. пределом f(x) в точке X0,
если для 0
()>0,
такое, что |f(x) - A|<
для x:
0< |X- ОДНОСТОРОННИЕ ПРЕДЕЛЫ
A=
СВОЙСТВА ПРЕДЕЛОВесли
|
НЕКОТОРЫЕ ТИПЫ ПРЕДЕЛОВПРЕДЕЛЫ ОТ РАЦИОНАЛЬНЫХ ДРОБЕЙесли Pn(x)=anxn+…+a1x+a0, Qm(x)=bmxm+…+b1x+b0, то 0, n<m – раздели Pn(x) и Qm(x)
1)
2)
ПРЕДЕЛЫ ОТ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
ПРЕДЕЛЫ ОТ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙпусть f(x) и g(x) иррациональные выражения
1)
2)
3)
|
НЕКОТОРЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ ПРАВИЛО ЛОПИТАЛЯ
Если
f(x)
и g(x)
существует при x:
0<|x-a|<ε
и существует
Замечание: 1) правило может быть применено многократно,
2)
случаи -,
0,
преобразованием сводят к
3)
случаи 1,
00,
0
логарифмированием исходного выражения
сводят к ЗАМЕНА ЭКВИВАЛЕНТНЫМИ ВЕЛИЧИНАМИЕсли f(x) ~ φ(x), a g(x) ~ ψ(x) при xa, то ,
Замечание: x ~ sin(x) ~ tg(x) ~ arcsin(x) ~ arctg(x) ~ ex – 1;
МЕТОД ВЫДЕЛЕНИЯ ГЛАВНОЙ ЧАСТИ
f(x)
и g(x)
имеют одинаковые главные части при
xa
до порядка n,
если f(x)
– g(x)=0(|x–a|n).
Если
Замечание:
1) другие неопределенности сводятся
к случаю
Основные
разложения: ex=1+
sin(x)=
|

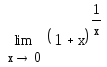 =e,
=e,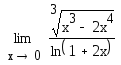 =
=