Проектирования

1. Принципы анализа инвестиционного проекта

2. Стоимость денег во времени. Сложный процент и дисконтирование

3. Показатели эффективности в проектном анализе

1. Принципы анализа инвестиционного проекта

Анализируя доходность инвестиционного проекта, целесообразно сравнивать две будущие альтернативные ситуации: а) фирма осуществила свой проект; б) фирма не осуществляла этот проект. Подобный прием часто называют «с проектом - без проекта». В модифицированном виде этот прием можно представить в виде формулы:

Р_инв=∆Р_пр - ∆С_пр ,

где Р_инв - доходность инвестиционного проекта;

∆Р_пр – изменения в выгодах/доходах благодаря проекту;

∆С_пр - изменения в затратах благодаря проекту.

Предположим, что у фирмы есть проект, рассчитанный на семь лет. Если фирма от него откажется, то ее доходы составят 50, а затраты - 40 млн. руб. В случае реализации проекта доходы возрастут до 90, а затраты - до 60 млн. руб. (табл. 34).

Таблица 34 – Результаты анализа инвестиционного проекта, млн. руб.

Показатели	Выгоды	Затраты	Доходность
С проектом	90	60	30
Без проекта	50	40	10
Изменения	40	20	20

Таким образом, реализация проекта повысит доходность фирмы на 20 млн. руб., несмотря на рост затрат на проект.

На рисунке 52, а видно, что площадь сектора А превышает площадь сектора Б, т.е. чистый доход фирмы Р при варианте выполнения проекта выше, чем при варианте «без проекта». Однако на практике чаще бывали случаи, когда чистые доходы фирмы понижаются, если она не реализует проект (рис. 52, б).

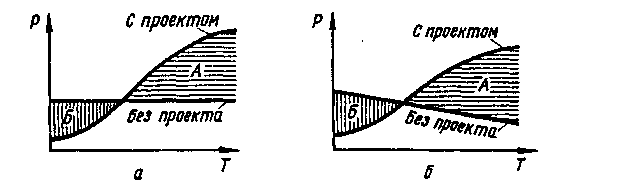
Рис. 52 - Метод «с проектом - без проекта»:

а - рост доходов при реализации

проекта и их неизменность при отказе от него; б - падение доходов

в случае отказа от проекта; Р - чистый доход, Т - годы

2. Стоимость денег во времени. Сложный процент и дисконтирование

Один из принципов проектного анализа состоит в том, что необходимо сопоставлять затраты и доходы (выгоды), возникающие в разное время. Так, затраты на проект осуществляются продолжительное время, а доходы от проекта, кроме того, возникают обычно после осуществления затрат.

Если 1 рубль, ссужается на один год, а не тратится сейчас, то это явится предпосылкой для того, чтобы через год вернулся не 1 рубль, а больше; поскольку рубль, истраченный сейчас, стоит больше, чем рубль через год. Таким образом, имеет место такое понятие, как стоимость денег во времени.

В экономическом и финансовом анализе используют специальный прием для измерения текущей и будущей стоимости одной денеж­ной мерой, который называется дисконтированием.

Дисконтирование является процессом, обратным начислению сложного процента. Процесс роста основной суммы вклада за счет накопления процентов называется начислением сложного процента, а сумма, полученная в результате накопления процентов, называется будущей стоимостью суммы вклада по истечении периода, на кото­рый осуществляется расчет. Первоначальная сумма вклада называется текущей стоимостью.

Предположим, что в банк положена 1 тыс. руб. при ставке 10% в год. Таким образом, текущая стоимость составляет 1 тыс. руб.

Если обозначить будущую стоимость FV; текущую стоимость PV; r - ставку процента; п - число лет, то: FV=PV(1+r)ⁿ (таблица 35).

Таблица 35 - Начисление сложного процента

Год	Будущая стоимость
1 2 3	1+0,1х1=1х1,101=1,1 1,1+0,1х1,1=1х1,12=1,21 1,21+0,1х1,21=1х1,13=1,33

Для того чтобы определить, каков должен быть первоначальный вклад, чтобы к концу третьего года он составил 1330 руб., исходя из ставки процента 10% в год, называемый текущей стоимостью будущей стоимости в 1330 руб., используется формула, обратная начислению сложного процента, представляющая собой процесс дисконтирования:

Текущая стоимость 1330 руб., полученных в будущем, равна:

PV=.

Таким образом, дисконтирование - это приведение потоков доходов и затрат на основе ставки дисконта к текущей (сегодняшней) стоимости.