2 Способ:

max π: 500=198+20,6Q,

Q=14,7.

Цена 400 руб. за единицу продукции. Минимальное значение средних валовых издержек равно 439 руб., т.е. выше сложившейся цены. Но цена выше минимального значения средних переменных издержек (328 руб.). Поэтому в краткосрочном периоде фирмы будет минимизировать убыток.

1 Подход:

=1406+198Q+10,3Q²-400Q,

=1406-202Q+10,3Q²,

min : =20,6Q-202=0,

Q=9,8.

2 Подход:

min : 4000=198+20,6Q,

Q=9,8.

Цена 300 руб. Ее уровень ниже минимального значения средних переменных издержек. Осуществлять производство и в краткосрочном периоде не целесообразно.

Фирма будет производить продукцию в краткосрочном периоде, если цена превысит 328 руб. за единицу. В интервале цены 328-439 руб. фирма будет получать убыток. Объем производства будет находиться в пределах 6,3-11,7 ед.

Если цена превысит 439 руб., фирма получит прибыль. Объем производства составит не менее 11,7 ед.

Предложение фирмы в краткосрочном периоде может быть выражено следующей формулой:

Q_S=0,0485 Р-9,6, (при Р>328 руб.).

В долгосрочном периоде, когда могут меняться все виды затрат, решение фирмы об объеме выпускаемой продукции будет приниматься иначе.

Если при существующей рыночной цене несколько фирм получают убытки и прекращают производство, предложение на рынке сокращается. Результатом сокращения предложения (при постоянном спросе) является повышение цены. Возросшая цена позволит фирмам, оставшимся в отрасли, получать экономическую прибыль. В условиях совершенной конкуренции, когда нет ограничений доступа на рынок, в отрасль вступят новые фирмы, привлеченные возросшей прибыльностью производства. В результате предложение возрастет, а цена сни­зится. При совершенной конкуренции такие колебания носят постоянный характер.

Равновесие на рынке будет достигнуто, когда у фирм не будет стимулов как для входа в отрасль, так и для выхода из нее. Это достигается при условии, если рыночная цена установится на уровне минимума средних валовых издержек и экономическая прибыль, таким образом, будет равна нулю.

Графическое решение представлено на рисунке 42. При цене Р_о объем производства фирмы составит Q_o. При таком объеме предельный доход равен предельным издержкам, а минимальные средние валовые издержки равны рыночной цене, экономическая прибыль равна нулю. При таких условиях фирма не изменяет объемы производства.

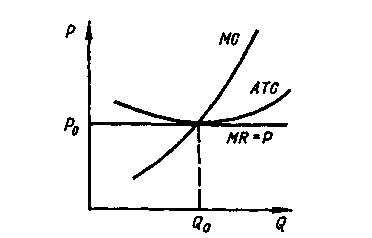
Рис. 42 - Долгосрочное равновесие фирмы в условиях

совершенной конкуренции

Математическая запись условия равновесия фирмы на конкурентом рынке:

P_o=min ATC(Q_o)=MC(Q_o)=MR(Q_o).

Изменения предложения в конкурентной отрасли при изменении спроса.

Предположим, что до изменения спроса на рынке существовало равновесие. График S на рисунке 43 представляет собой кривую предложения всех фирм, производящих данную продукцию, т.е. кривую предложения отрасли; D - кривая рыночного спроса; Р_о - равновесная рыночная цена, a Q_o - равновесный объем производства отрасли:

Q_o=D(P_o)=S(P_o).

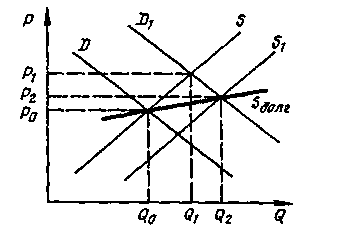
Рис. 43 - Кривая предложения отрасли в долгосрочном периоде:

D, D₁ - отрасле­вой спрос до и после изменения; S, S₁ - отраслевое

предложение до и после изменения; S_долг - долгосрочное

предложение отрасли

Если по каким-либо причинам спрос на данную продукцию возрастет, то кривая спроса сдвинется вправо до уровня D₁. Цена на рынке возрастет до Р₁:

Q₁=D₁(Р₁)=S(P₁).

Для отдельных фирм и отрасли это будет означать, что цена окажется выше минимума средних валовых издержек, а равенство цены и предельных издержек будет достигаться при большем объеме производства. Фирмы начнут получать эко­номическую прибыль, что создаст стимулы для расширения производства и вступления новых производителей в отрасль.

Вступление новых фирм, привлеченных возможностью получения экономической прибыли, сдвинет кривую предложения отрасли до S₁. В результате цена снизится и возникнет новое равнове­сие при цене Р₂ и объеме производства Q₂:

Q₂=D₁(Р₂)=S(P₂).

Если увеличение объема производства в отрасли не приводит к росту издержек, то кривая долгосрочного предложения будет горизонтальной. Однако в условиях ограниченности ресурсов вовлечение в производственный процесс все большего и большего их количества вызовет рост цен на них, поэтому Р₂>Р_о, а кривая долгосрочного предложения будет восходящей: Q_o=S_долг(Р_о); Q₂=S_долг(P₂); Q₂>Q₀.