
- •Экономико-математические методы и модели (курс лекций)
- •Isbn 5-7369-0373-3 © Векленко в.И., 2006 введение
- •Часть I. Экономико-математические
- •Классификация экономико-математических методов
- •1. Методы классической математики
- •Леция 2. Основы линейного программирования
- •1. Общие сведения о линейном программировании
- •2. Задача линейного программирования
- •3. Постановка задачи линейного программирования
- •Лекция 3. Решение и анализ задачи линейного программирования
- •Графический способ решения задачи
- •Симплексный метод и его алгоритм
- •Решение задачи симплексным методом
- •4. Симплекс-метод с искусственным базисом или м-метод
- •Оптимальных решений задач линейного программирования
- •Двойственная задача линейного программирования
- •2. Экономические свойства двойственных оценок
- •3. Анализ оптимального решения по последней симплексной таблице
- •Лекция 5. Распределительный метод решения задачи линейного программирования
- •Постановка и экономико-математическая модель распределительной (транспортной) задачи
- •2. Общая характеристика метода потенциалов
- •3. Решение транспортной задачи
- •Особые случаи решения транспортной задачи
- •Дополнительные ограничения в транспортной задаче
- •Лекция 6. Методы теории игр
- •Основные понятия теории игр
- •Матричные игры
- •Критерии оптимизации в играх с природой. Принятие решений в условиях неопределенности
- •Лекция 7. Методы управления запасами
- •Системы регулирования товарных запасов
- •Модель Уилсона
- •Задача 1
- •Решение
- •Модель планирования экономичного размера партии
- •Формулы модели экономичного размера партии:
- •Задача 2
- •Решение
- •Лекция 8. Балансовые методы и модели
- •Балансовый метод. Принципиальная схема межотраслевого баланса
- •2. Экономико-математическая модель межотраслевого баланса
- •3. Расчеты по модели межотраслевого баланса
- •Определение обратной матрицы Еn-а методом Жордана-Гаусса:
- •Задача 1.
- •Задача 2
- •Лекция 9. Сетевое планирование
- •Основные понятия сетевых методов
- •Методы построения сетевых моделей
- •Основные понятия сетевых методов
- •Методы построения сетевых моделей
- •Задача 1
- •Решение
- •Анализ сетевых моделей
- •Задача 2
- •Решение
- •4. График взаимосвязи работ во времени
- •Задача 3
- •Лекция 10. Методы и модели теории массового обслуживания
- •1. Общие понятия, определения и классификация методов и моделей в системах массового обслуживания
- •2. Модели разомкнутых систем
- •Часть II. Экономико-математические
- •2. Экономическая система
- •Моделирование экономических процессов
- •4. Экономико-математические модели
- •1. Законы спроса и предложения
- •2. Рыночная цена
- •3. Эластичность
- •Закон убывающей предельной полезности. Потребительское поведение
- •2. Эффект дохода и эффект замещения
- •3. Кривые безразличия
- •4. Бюджетные линии
- •Лекция 14. Модели издержек фирмы
- •2. Предельные издержки фирмы
- •Модели поведения фирмы в условиях совершенной конкуренции
- •2 Способ:
- •1 Подход:
- •2 Подход:
- •2. Модели поведения монополии
- •Лекция 16. Оптимальное распределение ресурсов фирмой
- •1. Предельная доходность ресурса
- •2. Предельные издержки ресурса
- •3. Выбор варианта сочетания ресурсов
- •Проектирования
- •1. Принципы анализа инвестиционного проекта
- •2. Стоимость денег во времени. Сложный процент и дисконтирование
- •3. Показатели эффективности в проектном анализе
- •1. Способы представления производственных функций
- •2. Экономико-статистическое моделирование
- •3. Экономические характеристики производственных функций
- •Лекция 19. Модель общего рыночного равновесия эрроу-гурвица
- •1. Алгоритм построения модели
- •2. Проведение модельных расчетов
- •Р. Солоу
- •1. Накопление капитала
- •2. Рост народонаселения
- •3. Научно-технический прогресс
- •Содержание
Модель Уилсона
Математические модели управления запасами (УЗ) позволяют найти оптимальный уровень запасов некоторого товара, минимизирующий суммарные затраты на покупку, оформление и доставку заказа, хранение товара, а также убытки от его дефицита. Модель Уилсона является простейшей моделью управления запасами. Она описывает ситуацию закупки продукции у внешнего поставщика, которая характеризуется следующими допущениями:
интенсивность потребления является постоянной величиной;
заказ доставляется с одного и того же склада;
время поставки заказа является известной и постоянной величиной;
каждый заказ поставляется в виде одной партии;
затраты на осуществление заказа не зависят от размера заказа;
затраты на хранение запаса пропорциональны его размеру;
отсутствие запаса (дефицит) является недопустимым.
Входные параметры модели Уилсона:
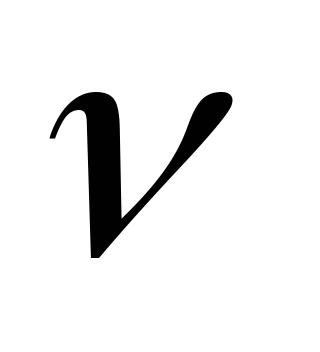 –интенсивность
(скорость) потребления запаса,
[ед.
тов./ед.t];
–интенсивность
(скорость) потребления запаса,
[ед.
тов./ед.t];s – затраты на хранение запаса, [
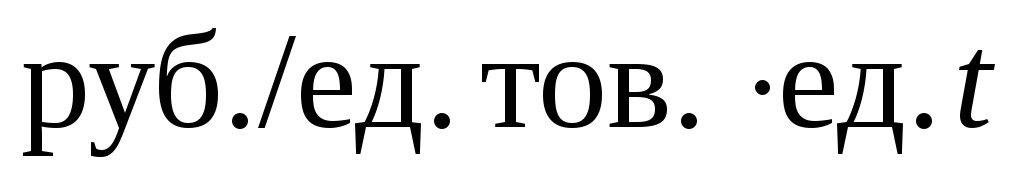 ];
];K – затраты на осуществление заказа, включающие оформление и доставку заказа, [руб.];
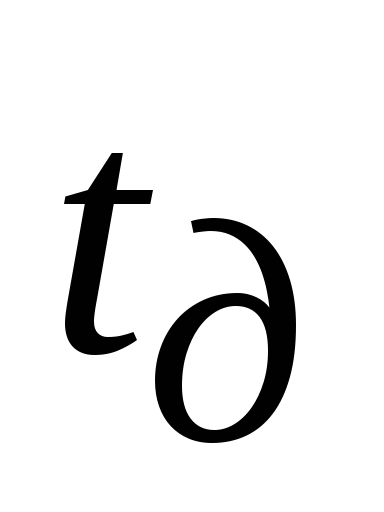 –время
доставки заказа, [ед.t].
–время
доставки заказа, [ед.t].
Выходные параметры модели Уилсона:
Q – размер заказа, [ед. тов.];
L – общие затраты на управление запасами в единицу времени, [руб./ед.t];
 –период
поставки, т.е. время между подачами
заказа или между поставками, [ед. t];
–период
поставки, т.е. время между подачами
заказа или между поставками, [ед. t];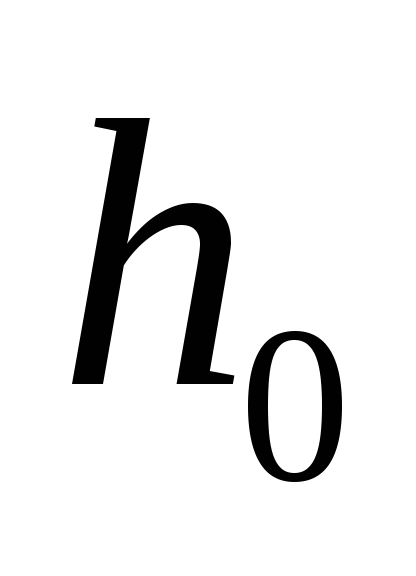 –точка
заказа, т.е.
размер запаса на складе, при котором
надо подавать заказ на доставку очередной
партии, [ед. тов.].
–точка
заказа, т.е.
размер запаса на складе, при котором
надо подавать заказ на доставку очередной
партии, [ед. тов.].
Циклы изменения уровня запаса в модели Уилсона графически представлены на рис. 5. Максимальное количество продукции, которое находится в запасе, совпадает с размером заказа Q.
Точка
заказа
h0
Q
tд
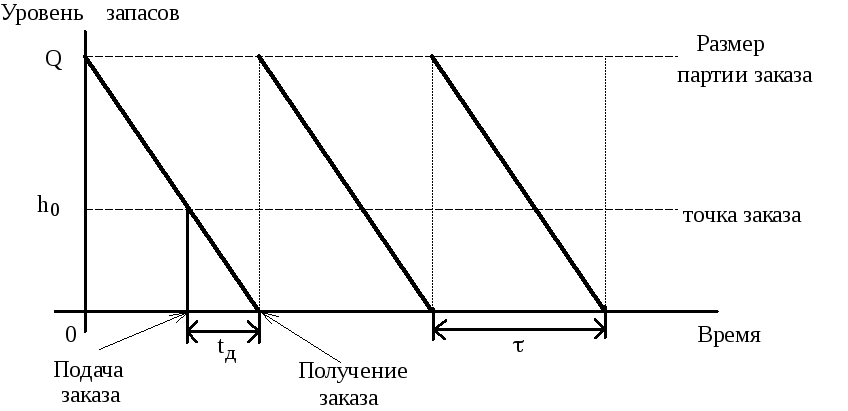
Рис. 5 - График циклов изменения запасов в модели Уилсона
|
|
|
где
![]() –
оптимальный размер заказа в модели
Уилсона;
–
оптимальный размер заказа в модели
Уилсона;
![]() ;
;
![]() ;
;
![]()
![]() .
.
График затрат на управление запасами в модели Уилсона представлен на рис. 6.
L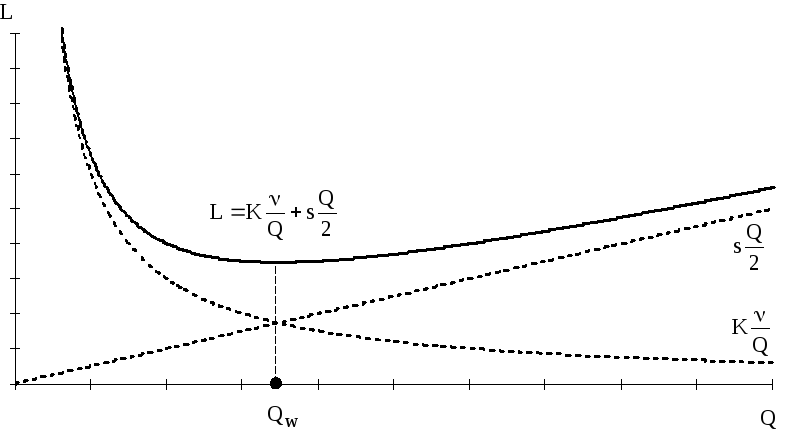
Рис. 6 - График затрат на управление запасами в модели Уилсона
Задача 1
Потребность птицефабрики в комбикорме 2 т в сутки. За доставку комбикорма птицефабрика должна заплатить 10 тыс. руб. Время доставки заказа от комбикормового завода составляет 12 рабочих дней (при 6-дневной рабочей неделе). По оценкам специалистов, издержки хранения в год составляют 400 руб. за 1 т комбикорма. Необходимо определить: какой объем комбикорма должна заказывать птицефабрика для одной поставки; частоту заказов; точку заказа (Qw, I, ho).
Решение
Примем
за единицу времени год, тогда
![]() 2
2![]() 365
= 730 т в год,
365
= 730 т в год,![]() тыс. руб.,
тыс. руб.,![]() 400
400![]() .
Используем модель Уилсона:
.
Используем модель Уилсона:
![]()
Годовые затраты на управление запасами равны:
тыс.
![]() руб.
руб.
Подача каждого нового заказа должна производиться через:
![]() года
или
года
или
![]() дней.
дней.
Заказ следует подавать при уровне запаса, равном:
![]() ,
v
= 2
т/сутки,
,
v
= 2
т/сутки,
т.е. эти 26 т будут потреблены в течение 13 дней, пока будет доставляться заказ.
Модель планирования экономичного размера партии
Модель Уилсона, используемую для моделирования процессов закупки продукции у внешнего поставщика, можно модифицировать и применять в случае собственного производства продукции. На рис.7 схематично представлен некоторый производственный процесс, в котором на первом станке производится партия деталей, а затем она используется на втором станке.
![]()
Рис.7 - Схема производственного процесса
Входные параметры модели планирования экономичного размера партии:
 –интенсивность
производства продукции первым станком,
[ед.тов./ед. t];
–интенсивность
производства продукции первым станком,
[ед.тов./ед. t];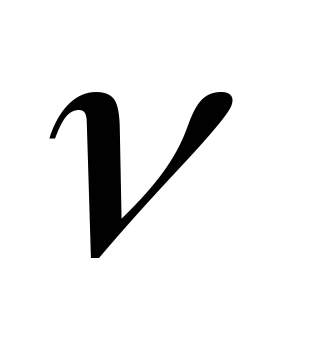 –интенсивность
потребления запаса, [ед.тов./ед. t];
–интенсивность
потребления запаса, [ед.тов./ед. t];s – затраты на хранение запаса, [руб./ед.тов. ед. t];
K – затраты на осуществление заказа, включающие подготовку (переналадку) первого станка для производства продукции, потребляемой на втором станке, [руб.];
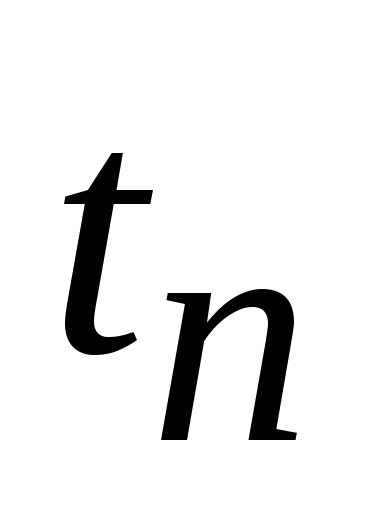 –время
подготовки производства (переналадки),
[ед. t].
–время
подготовки производства (переналадки),
[ед. t].
Выходные параметры модели планирования экономичного размера партии:
Q – размер заказа, [ед. тов.];
L – общие затраты на управление запасами в единицу времени, [руб./ед. t];
 –период
запуска в производство партии заказа,
т.е. время между включениями в работу
первого станка, [ед. t];
–период
запуска в производство партии заказа,
т.е. время между включениями в работу
первого станка, [ед. t];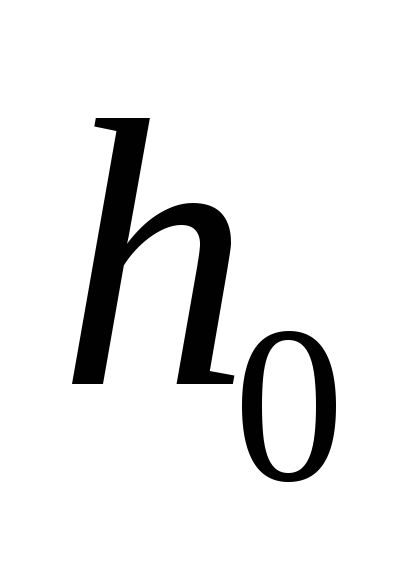 –точка
заказа, т.е. размер запаса, при котором
надо подавать заказ на производство
очередной партии, [ед. тов.].
–точка
заказа, т.е. размер запаса, при котором
надо подавать заказ на производство
очередной партии, [ед. тов.].
Изменение уровня запасов происходит следующим образом (рис. 8):
в течение времени
 работают оба станка, т.е. продукция
производится и потребляется одновременно,
вследствие чего запас накапливается
с интенсивностью (
- v)
;
работают оба станка, т.е. продукция
производится и потребляется одновременно,
вследствие чего запас накапливается
с интенсивностью (
- v)
;
в течение времени
 работает только второй станок, потребляя
накопившийся запас с интенсивностью
v.
работает только второй станок, потребляя
накопившийся запас с интенсивностью
v.
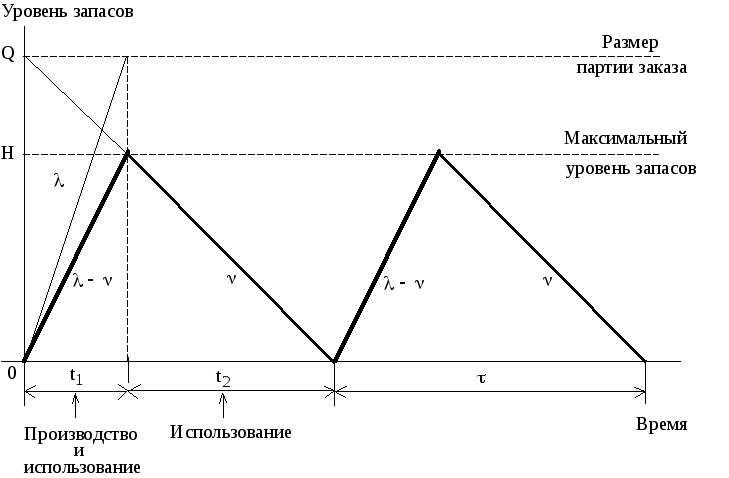
Рис. 8 - График циклов изменения запасов в модели планирования
экономичного размера партии
