6. Производная вектора

Пусть вектор меняется по известному закону со временем.

.

Производная такого вектора по аргументу tвычисляется как производная сложной функции

где: ,и— единичные векторы направленийx, y, z.

2. Кинематические характеристики криволинейного движения

   1. Скорость движения

Зададим криволинейное движение частицы Мзависимостью её радиус-вектора от времени (рис. 2.7):

. (2.7)

Рис. 2.7

Пусть и— радиус-векторы частицы в моменты времениt и (t + t) (рис. 2.8). Разность этих векторов называется вектором перемещения частицы.

M

Рис. 2.8

По определению, вектором средней скоростидвиженияв интервале времени отtдоt+tназывается отношение вектора перемещения ко времени, за которое оно произошло:

. (2.8)

Направление вектора средней скорости совпадает с направлением вектора перемещения .

Если уменьшать интервал времени, устремляя его к нулю, то вектор средней скорости стремится к значению, которое называется мгновенная скорость:

(2.9)

Учитывая (2.7) запишем вектор мгновенной скорости в виде векторной суммы её составляющих по координатам x,y,z:

(2.10)

где: V_x,V_y,V_z— проекции вектора скорости на осиx,y,z(рис. 2.9)

Рис. 2.9

Модуль вектора скорости

Вектор мгновенной скорости всегда направлен по касательной к траектории (рис. 2.10)

Рис. 2.10

2. Ускорение. Нормальное и тангенциальное ускорение. Радиус кривизны траектории

Движение по криволинейной траектории всегда происходит с переменной скоростью. Пусть — скорость частицы в момент времениt, а— скорость частицыtсекунд спустя.

Отношение вектора изменения скорости к промежутку времени, за который это изменение произошло, определяет вектор среднего ускорения движения

(2.11)

.

Вектор среднего ускорения всегда направлен в сторону вогнутости траектории (рис. 2.11)

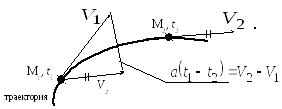
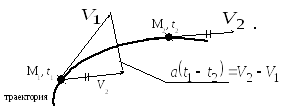
Рис. 2.11

Предел среднего ускорения при t0 называетсявектором мгновенного ускорениячастицы в момент времени t.

. (2.12)

Скорость можно представить векторной суммой её составляющих (см. (2.10))

.

Тогда вектор ускорения можно записать так:

. (2.13)

Здесь ,,.

Модуль вектора ускорения

.

Часто проецируют вектор ускорения не на оси неподвижной системы координат, а на направления касательное () и нормальноек траектории (рис. 2.12):

. (2.14)

Здесь а_ иа_n— проекции вектора ускорения,и— единичные векторы тангенциального (касательного) и нормального направлений.

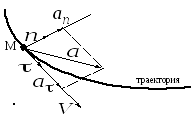
Рис. 2.12

Смысл такого представления ускорения (2.14) в том, что тангенциальное ускорение а_определяет изменение вектора скорости только по величине, а нормальная составляющаяа_nсвязана с изменением вектора скорости только по направлению. Покажем, что это именно так.

Пусть за время dtскорость частицы изменилась наотдо.

(2.15)

Представим сначала, что нормальное ускорение отсутствует . Тогда изменение скорости связано только с тангенциальным ускорением:

.

Полученный результат означает, что изменение скорости совпадает по направлению с самой скоростью!

Таким образом, скорость, сохраняя свое направление, будет меняться только по величине

или

(2.16)

Касательная составляющая ускорения равна производной модуля скорости по времени.

Теперь пусть отсутствует касательное ускорение . В этом случае:

Новое значение скорости равно:

Возведем эту скорость в квадрат

В правой части этого уравнения вторым слагаемым можно пренебречь по сравнению с V²(t), а в третьем слагаемом скалярное произведение взаимно-перпендикулярных векторов равно нулю. Таким образом, за времяdtскорость частицы не изменилась по величине

!

Это означает, что нормальная составляющая ускорения определяет изменение вектора скорости только по направлению. Известно, что численно нормальное (центростремительное) ускорение равно отношению квадрата линейной скорости к радиусу кривизны траекторииR:

. (2.17)

Чтобы пояснить этот параметр R, рассмотрим небольшой фрагмент плоской криволинейной траектории. В близких точках М и М’ проведём касательные к траекториии’, а к ним восстановим перпендикуляры N и N’ (рис. 2.13). Они пересекаются в точке C’.

Рис. 2.13

Начнем приближать точку М’ к М. При этом угол между нормалями и дугаустремляются в пределе к нулю. По определению радиусом кривизны плоской линии называется следующий предел

(2.18)

В процессе этой операции точка C’ сместится в новое положение — точку С — центр кривизны.

Теперь обратимся к рассмотрению важного частного случая криволинейного движения.