3. Момент инерции тела. Теорема Гюйгенса-Штейнера. Примеры вычисления моментов инерции тел

Момент инерции тела аддитивная величина, равная сумме моментов инерции всех частиц тела:

.

Здесь m_i— массаi-той частицы, которую можно связать с плотностью вещества_iи объёмом частицы:

m_i=_iV_i.

Тогда .

Если тело однородно, то есть его плотность повсюду одинакова, то можно вынести за знак суммы:

.

Разделяя тело на всё более мелкие частицы, сведём задачу отыскания момента инерции к вычислению интеграла:

.

Интегрирование проводится по всему объёму тела V.

В качестве примера вычислим момент инерции тонкого однородного стержня относительно оси z, проходящей через его центр масс — точку С (рис. 9.3). Длина стержня —l, его масса —M.

На расстоянии x от оси вращения выделим элемент dx, масса которогоdm=.

0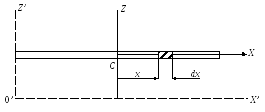

Рис. 9.3

Момент инерции этой частицы стержня равен:

.

Вычислив подобным образом, моменты инерции всех элементов стержня, сложим их, взяв интеграл:

.

Таким образом:

I_z=. (9.7)

Интегрирование проведено по xв пределах отдо.

Как изменится момент инерции этого стержня, если ось вращения перенести в другое место? Провести её, например, через край стержня?

В этом случае прежний интеграл нужно рассмотреть в пределах от 0 до l:

. (9.8)

Новое значение момента инерции того же стержня заметно возросло. Связано это с тем, что момент инерции тела определяется не только его массой, но и её распределением относительно оси вращения.

Вычислим момент инерции ещё одного тела: сплошного цилиндра относительно его геометрической оси.

Рис. 9.4

Пусть M— масса, аR— радиус цилиндра (рис. 9.4). Выделим в этом цилиндре цилиндрический слой радиусомrи толщинойdr. Масса этого слоя:

dm=dV=2rdrl,

где: — плотность материала цилиндра;

l— его длина.

Все частицы этого слоя находятся на одинаковом расстоянии от оси вращения — геометрической оси цилиндра, значит, момент инерции слоя равен:

dI = dm  r² =   2r  dr  l  r².

Для отыскания момента инерции цилиндра проинтегрируем последнее выражение:

.

Отметим, что R²l=V— объём цилиндра, аR²l=V=M— его масса.

Тогда момент инерции цилиндра относительно его геометрической оси можно окончательно записать в таком виде:

.

Теорема Гюйгенса-Штейнера

Момент инерции тела относительно произвольной оси (I) равен сумме момента инерции I_c относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела М на квадрат расстояния между осями:

I=I_c+Ma², (9.9)

где а— расстояние между осями.

На рисунке 9.5 оси вращения перпендикулярны плоскости чертежа: через точку 0 проходит произвольная ось; параллельная ей ось проведена через центр масс тела — точку С. Расстояние между осями —а.

Выделим элемент тела массой m_i. Его момент инерции относительно оси 0 равен:

. (9.10)

Как следует из рисунка , откуда:

. (9.11)

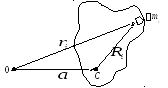
Рис. 9.5

Теперь момент инерции частицы m_i(9.10) можно представить такой суммой:

.

Для отыскания момента инерции всего тела, нужно сложить моменты инерции всех его частиц:

. (9.12)

Здесь за знак суммы вынесена постоянная величина — расстояние между осями а. Первое слагаемое справа=Ма², так как=М— масса тела. Второе слагаемое=I_С— момент инерции тела, относительно оси, проходящей через центр масс. Третье слагаемое равно нулю, так как суммаравна произведению массы тела на вектор, проведённый от оси С к центру масс тела. Но ось С проходит через центр масс, поэтому= 0 и=М= 0.

Собрав эти результаты в уравнение (9.12), получим выражение теоремы Гюйгенса-Штейнера:

I_O=I_C+Ma².

Эта теорема значительно упрощает задачу вычисления моментов инерции.

Известен, например, момент инерции стержня относительно оси, проходящей через его центр масс (9.7):

.

Воспользовавшись теоремой Гюйгенса-Штейнера, легко вычислим момент инерции этого же стержня относительно оси z’, проходящей, например, через край стержня (рис. 9.3):

I_z’=I_z+Ma²,a=l/2.

.

Это значение момента инерции совпадает с результатом (9.8), который был получен методом прямого интегрирования.