Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Магнитогорский государственный технический университет им. Г.И.Носова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Uchebnye_karty_Chast_2

.pdf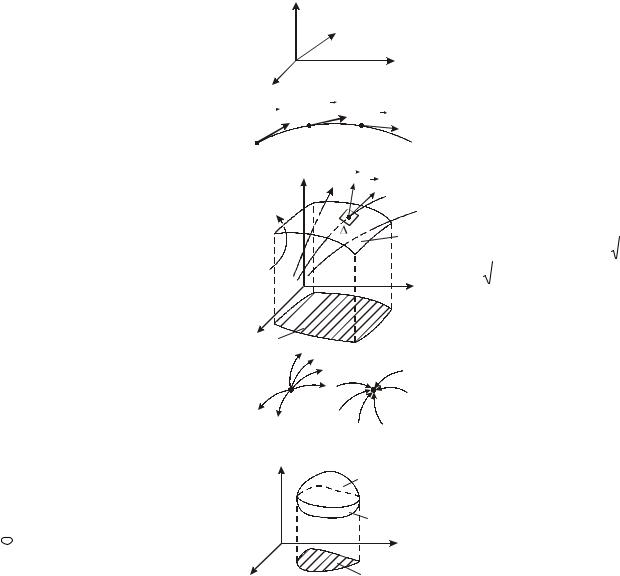

Скачиваний:

Добавлен:

11.02.2015

Размер:

1.24 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

18. Векторное поле. Характеристики векторного поля

Понятие

Определение и назначение

Геометрическое изображение

Вычисление

Каждой точке M (x, y, z)

M(x,y,z)

P(x, y, z), Q(x, y, z), R(x, y, z) – проекция вектора

(M )

1.Векторное

соответствует значение

поле a

векторной функции

a(M)

на оси ox , oy , oz

a = {P(x, y, z),Q(x, y, z), R(x, y, z)}

a(M2)

2.векторная

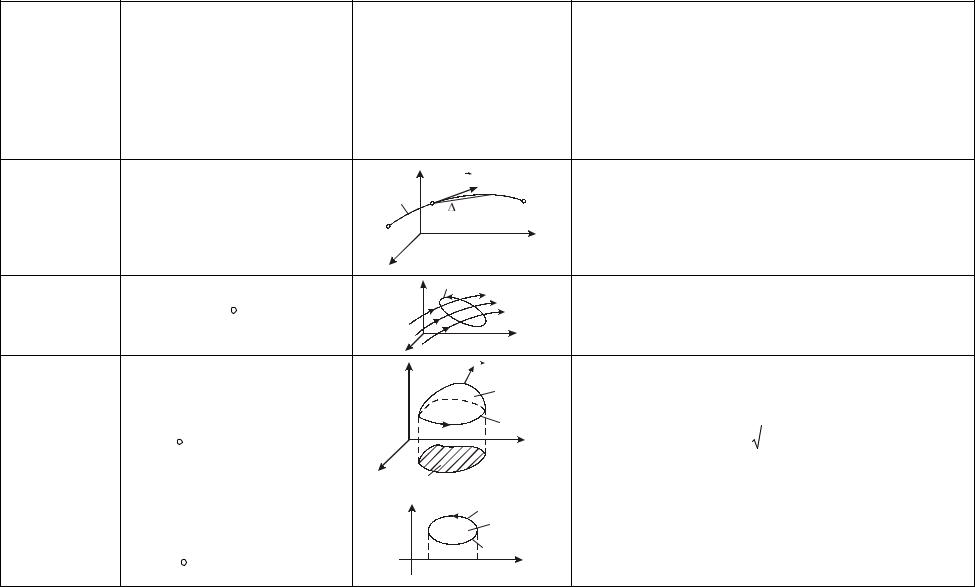
Линия, во всякой точке которой

a(M1)

a(M )

Q(x, y, z)

R(x, y, z)

(силовая) линия

вектор a направлен по

P(x, y, z)

поля a

касательной к ней.

Система дифференциальных уравнений, определяющая

векторные линии

a(Mi )

a = {P,Q, R}

П =

∞ R

Q : z = f (x, y) z − f (x, y) = 0

′,− f

′,1}

lim

∑a(Mi ) ni0 qi =

grad(z − f (x, y))

{− f

max qi →0 i−1

0 =

grad(z − f (x, y))

3.Поток поля a

( fx′)2 + ( f ′)2 +1

R 0

через

= ∫∫a(M )n

(M )dq

dq =

( f

′)2

+ ( f ′)2 +1 dxdy

поверхность Q

R 0

- единичный вектор

П = ∫∫[P(x, y,z)(− fx′) + Q(x, y, z)×(− fy′) + R(x, y, z)]dxdydz,

где n

нормали к поверхности

Dxy

где z = f (x, y)

Dxy

= {P,Q, R}

R R

поля

diva = a =

, =

i +

j +

k -

V→0 V ∫∫

4. Дивергенция

diva(M ) = lim

a n0dq

∂P

∂Q

∂R

∂

∂ R

(расходимость

∂x

∂y

∂z

∂x

∂y

∂z

V -объем, ограниченный

(M ) > 0;

(M )< 0

оператор Гамильтона, ( - набла)

поля)

поверхностью

diva

Поле a - соленоидальное (трубчатое), если diva = 0

т. M - исток;

т. M - сток

z=f2 (x,y)

Формула Гаусса –

= {P,Q, R}

5. Поток поля a

Остроградского (связь между

R: f1 (x, y) ≤ z ≤ f2 (x, y)

через

потоком и дивергенцией поля)

z=f1 (x,y)

замкнутую

∂P

∂Q

∂R

поверхность Q

∫∫a

dq =

∫∫∫diva dV

П = ∫∫∫(

)dxdydz

∂x

∂y

∂z

Dxy

a = {P,Q, R}

∂R

−

∂Q R

∂P

−

∂R R

∂Q

−

∂P R

rota

= × a

rota

∂y

∂z

∂x

6. Ротор (вихрь)

∂z

∂y

Поле a(M) – потенциальное (безвихревое) если rota = 0

∂

поля a

∂x

∂y

∂z

U(M ) = ∫P(x, y0 , z0 )dx + ∫Q(x, y, z0 )dy + ∫R(x, y, z)dz + C -

P(x, y, z)

Q(x, y, z)

R(x, y, z)

потенциал поля a(M )

= {P,Q, R}

7. Работа поля

a(M)

Г : x = x(t), y = y(t), z = z(t),α ≤ t ≤ β

∞

a(M ) по

A = lim

)

перемещению

∑a(Mi

= ∫a

точки вдоль

D( l)→0

i=1

A = ∫[P(x(t), y(t), z(t))x

(t) +Q(x(t), y(t), z(t))y

(t) +

кривой L

+ R(x(t), y(t), z(t))z' (t)]dt

8. Циркуляция

Вычисляется аналогично пункту 7.

поля a по

Ц = ∫a

А=Ц, если Г – замкнутый контур.

контуру L

(В потенциальном поле Ц=0).

9. Циркуляция

a = {P,Q, R}

grad(z − f (x, y))

поля a(M ) по

Формула Стокса устанавливает

Q : z = f (x, y),n0

замкнутому

связь потока вектора rota с

grad(z − f (x, y))

контуру L ,

циркуляцией поля

являющемся

Ц = ∫a dl

= ∫∫rot a

0 dq

rota = × a

(см п. 5), dq = 1+ ( fx )

+ ( f y

)

dxdy

границей

Ц = ∫∫rota n0dq вычисляется как в пункте 3

поверхности Q

Dxy - проекция Q на xoy

Формула Грина устанавливает

10.Циркуляция

y=f2(x)

a = P(x, y)i + Q(x, y) j

связь вихря с циркуляцией

плоского поля

D : f1 (x) ≤ y ≤ f2 (x)

плоского поля

a по

∂Q

∂P

y=f1(x)

∂Q ∂P

замкнутому

∫

∫∫

0 a

∫∫

Ц = A =

a dl

−

dxdy

Ц = A =

−

dxdy

контуру L

D ∂x

∂y

∂x

∂y

19. Дифференциальные уравнения первого порядка

Тип уравнения

Вид уравнения

Признак типа уравнения

Указания к решению уравнения

а) y = ∫ f (x)dx + c

а)

y′ =

f (x)

а) нет явно y

б)

∂y

= p(x) q(y) ∫

∂y

= ∫ p(x)dx + c

1. Уравнение с

б)

f (x, y) = p(x) q(y)

разделяющимися

б)

y′ =

f (x, y)

∂x

q(y)

в)

P(x, y) = p1

(x) p2 (y),

p1 (x) p2 (y)dx + q1(x) q2 (y)dy = 0

переменными

в)

P(x, y)dx + Q(x, y)dy = 0

в)

Q(x, y) = q1

(x) q2 (y)

∫

(x)

dx + ∫

q2 (y)

dy = c

q (x)

(y)

а)

= u y = u x, y′ =

x + u

f (tx,ty) = t0 f (x, y) = f (1,

а)

)

а) y′ = f (x, y)

2. Однородное

уравнение

б) P(x, y)dx + Q(x, y)dy = 0

P(tx,ty) = tk P(x, y)

x = f (1,u) − u уравнение типа 1

б)

P(x, y)

Q(tx,ty) = tk Q(x, y)

б)

y′ = −

= f (x, y) уравнение вида 2 а)

Q(x, y)

∫P(x, y0)dx + ∫Q(x, y)dy = c или

3. Уравнение в

∂P

∂Q

P(x, y)dx + Q(x, y)dy = 0

полных

∂y

∂x

∫P(x, y)dx + ∫Q(x0, y)dy = c ,

дифференциалах

где (x0, y0) точка области определения P(x, y) и Q(x, y)

y = u v, y′ =

v +

u +

p(x) uv

y′ = f (x, y)

q(x)

4. Линейное

или

f (x, y) = p(x) y + q(x)

= p(x) u,

u = e−∫ p(x)dx

= ϕ(x)

уравнение

y′ + P(x)y = q(x)

= ∫

q(x)

u = q(x)

dx + c

y = u v

ϕ(x)

5. Уравнение

y′ = f (x, y)

f (x, y) = p(x) y + q(x) yk ,

Бернулли

или

Решается тем же методом, что тип 4.

(линейное

k ≠ 0,k ≠ 1

y′ + P(x)y = q(x)yk

обобщенное)

Замечание. Если удобнее рассматривать уравнение не в виде y′ = f (x, y) , а в виде x′ = f (x, y), где x′ =

, то всюду в указаниях к

y′

решению уравнения y′ = f (x, y) надо поменять местами x и y .

20. Виды дифференциальных уравнений высших порядков, допускающих понижение порядка

Вид уравнения

Признаки

Метод понижения порядка

Частный вид при n=2

нет явно

Последовательное интегрирование (n-

y′′ = f (x)

последовательное

1. y

(n)

= f (x)

или F(x, y

(n)

) = 0

интегрирование (2 раза)

y, y′, y′′,...y(n−1)

квадратур)

y = ϕ(x,c1,c2 )

Подстановка

F(x, y′, y′′) = 0

нет явно

y(k) = z,

z = z(x)

2. F(x, y

(k)

, y

(k+1)

,...y

(n)

) = 0

явно нет y

y, y′, y′′,...y(k−1)

. . . . . . . . . . . . . . .

′

= z(x) ,

′′

= z

′

F(x,z, z

′

= 0)

y(n) = z(n−k) (x)

Подстановка y′ = P,

P = P(y)

F(y′, y′′) = 0

явно нет x

′

′′

(n)

) = 0

явно нет x

y′ = P(y),

3. F(y, y , y , y

y′′ =

P, y′′′ =

P2 +

P,...

y′′ =

P F(P,P′) = 0

Применяются последовательно

′

′′

4. F(y(k) , y(k+1) ,...y(n) ) = 0

подстановки y(k) = z(x) и z′ = P ,

обладает признаками видов

F(y , y

) = 0

2 и 3

P = P(z)

y′ = z , z = z(x)

21. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами

Вид уравнения:

Характер корней характеристического уравнения

Корни

Корни действительные,

Корни комплексные,

Корни комплексные, есть

действительные,

различные

y(n)

+ p

y(n−1) +...+ p

y = 0

есть повторяющиеся, т.е.

повторяющиеся

различные,

k1,2 = α1 ± β1 i

= k

= ... = k

= k

α ± β i

- пара корней

pi - числа

т. е.

k3,4 = α 2 ± β 2 i и т. д.

кратности m

≠ k2 ≠ k3

≠ ... ≠ kn

(корень кратности m)

= c1 y1 + c2 y2 + ...+ cn yn - общее

Вид частных решений y1, y2 , y3...yn , соответствующих корням характеристического уравнения

решение денного уравнения, где

y1 = e

k x

α1 x

αx

c ,c

...c

- произвольные постоянные,

y1 = ek1 x ,

,k x

y1 = e α1 x

cosβ1x,

y1 = e

αx cosβx,

y2 = e

k2 x

y2 = x e , ,

y2 = e

sinβ1x,

= e

sin βx,

y1 , y2 , y3 ...yn - фундаментальная система

y3 = x2 ek x ,

y3 = eα2 x

cosβ2 x,

= x eαx cosβx,

решений данного уравнения.		M			M	. . . . . . . . . . . .			M
k n + p1 k n−1 +...+ pn = 0	-	yn = ekn x	ym = xm−1 ek x				ym−1 = xm−1 eα x cosβx
k n + p1 k n−1 +...+ pn = 0	-		y		= ekm+1 x		ym = x	m−1	e	α x	sinβx
характеристическое уравнение			y	m+1	= ekm+1 x		ym = x		e		sinβx
характеристическое уравнение				m+1
			. . . . . . . . . . . .

22. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами

Вид уравнения:

y(n) + p1 y(n−1) +...+ pn y = f (x)

Структура общего решения: y = y + y* ,

где y - общее решение соответствующего однородного уравнения,

y* - частное решение неоднородного уравнения.

Если y1 - частное решение уравнения

y(n) + p1 y(n−1) +...+ pn y = f1 (x) y2 - частное решение уравнения

y(n) + p1 y(n−1) +...+ pn y = f2 (x) , то y1+ y2 - частное решение

уравнения

y(n) + p1 y(n−1) +...+ pn y = f1 (x) + f2 (x)

Метод вариации произвольных постоянных

Метод подбора частного решения

Если y1, y2 ,...yn

- фундаментальная система

f (x) = eα x [P (x) cosβx + Q (x) sinβx]-

решений соответствующего однородного

специальный вид правой части

уравнения, то общее решение неоднородного

неоднородного уравнения (пусть n > m)

уравнения находится по формуле

Частное решение y* ищется в виде

y = c1 (x) y1 +...+ cn (x) yn ,

= xr eα x

cos βx +

sin βx]

[P (x)

(x)

если

= c1 y1 + c2 y2 + ...+ cn yn

где r – кратность корней α ± β i

где ci (x),(i = 1,2...n) находится из системы

характеристического уравнения:

уравнений

n−1

Pn (x) = An x

+ An−1 x

+ ...+ A1 x + A0

(x) yi

Qn (x) = Bn xn + Bn−1 xn−1 +...+ B1 x + B0

∑ci′

= 0,

i=1

То есть y

зависит от правой части

∑ci′(x) yi′ = 0,

f (x) и от корней характеристического

i=1

ci (x) = ∫ci′(x)dx + ci ,i = 1,2...n

уравнения.

(x) yi

(n−2) = 0,

∑ci′

i=1

(x) yi

(n−1) = f (x)

∑ci′

i=1

Частный случай: n = 2

y = c1 (x) y1 + c2 (x) y2 ,

= c1 y1 + c2 y2

где c1(x) и c2 (x) находятся из системы уравнений

c′

(x) y + c′

(x)

= 0,

найти c′

(x) и c′ (x)

(x)

= f (x)

c′

(x) y′ + c′

′

c1(x) = ∫c1′(x)dx + c1, c2 (x) = ∫c2′ (x)dx + c2 ,

где c1,c2 - постоянные

23. Числовые ряды. Основные понятия

№		Понятие	Определение и обозначение
п/п		Понятие	Определение и обозначение
п/п
			∞
1.	Ряд		∑Un	= U1 +U2 +U3 +...+Un + ...
			n=1
2.	Члены ряда, общий ( n – ый ) член		U1 ,U2 ,U3 ,...Un - бесконечная числовая
2.	ряда		последовательность, где Un = f (n)
	ряда		последовательность, где Un = f (n)

			S1 = U1,
			S2 = U1 +U2 ,
3.	Частичные суммы ряда		S3 = U1 +U2 +U3 ,
3.	Частичные суммы ряда

			Sn = U1 +U2 +U3 + ...+Un ,

4.	Последовательность частичных сумм		S1, S2 , S3 ,...Sn ,...

							∞
5.	Сходящиеся ряды		lim Sn		= S , где S – сумма ряда
5.	Сходящиеся ряды		lim Sn		= S , где S – сумма ряда		∑Un	= S
			n→∞				n=1
							n=1
			lim Sn	=	∞
6.	Расходящиеся ряды		lim Sn	=
			n→∞		не существует
			U +U	2 +U3 +...+Un		+Un+1 +Un+2	+...+
7.	Остаток ряда		14444244443			14424443
7.	Остаток ряда				Sn	Rn
			Rn = U n+1 +Un+2 +...
		Основные свойства сходящихся рядов
∞
∑Un		сходится	Rn - сходится
n=1
∞			∞
∑Un		сходится, S – его сумма	∑λ Un сходится, λS - его сумма
n=1			n=1
∞			∞
∑Un		сходится, S – его сумма	∑(Un ±Vn ) - сходится
n=1			n=1
∞
∞
∑Un		сходится, σ – его сумма	S + σ - его сумма
n=1
		Необходимый признак сходимости ряда
∞
∑Un		- сходится	limUn = 0
n=1
			∞
Замечание: limUn ≠ 0			∑Un - расходится

n=1

24. Числовые ряды с положительными членами

∞

Определение ∑Un

= U1 +U2 +U3 +...+Un +..., Un

> 0, n, Un - действительные числа

n=1

∞

1 = 1+ 1 + 1 + ... + 1 + ... расходится

Гармонический ряд ∑

n=1 n

Обобщенный гармонический ряд

∞ 1

при

p > 1− сходится

(p > 0)

∑

Некоторые ряды и их

n=1 n p

p ≤ 1−

расходится

(a ≠ 0)

поведение

∞

∑a qn

q < 1− сходится S

Ряд геометрический

при

1- q

n=0

q ≥ 1− расходится

В частности при a = 1,

q = 1 ряды

1+1+1+ ...+1+ ...

расходится

−1+1−...+ (−1)

+...

Достаточные признаки сходимости числовых рядов с положительными членами

Признаки сравнения

Интегральный признак Коши

Признак Даламбера

Признак Коши

∞

∑Un

= U1 +U2

+U3 + ...+Un + ...

(1)

∑Un ,

∑Un

= U1 +U2 +...+Un +Un+1...

∑Un

= U1 + U2

+ ... + Un ...

n=1

∞

U1 ≥ U2 ≥ U3 ≥ ... ≥ Un ≥ ...

lim Un+1 = l

∑Vn

= V1 +V2 +V3 + ...+Vn

+...

(2)

lim n Un = l

n=1

n→∞ U

f (x) x > 1 : непрерывная,

n→∞

∞

положительная,

1. lim

= A(0 < A < ∞)

∑Un

и ∑Vn

а) l < 1 ∑Un

- сход.

а) l < 1 ∑Un

- сход.

n→∞ U

n=1

невозрастающая

f (n) = Un

n=1

= 0 ,

lim Vn = 0

где

lim Un

одновременно

∞

n→∞

сходятся или

б) l > 1 ∑Un

- расход.

б) l > 1 ∑Un

- расход.

(при

A = 1 U n Vn )

расходятся

n=1

∞

Замечание:

2. а) Un

≤ Vn ,∑Vn сход.

∑Un

сход

1. Если l =1, то признак Даламбера и Коши не дают ответа о

∞

сход.

n=1

A ∑Un −

∫

n=1

поведении ряда.

∞

f (x)dx =

∞

2. Признак Даламбера иногда используется без предельного

б) Un

≤ Vn ,∑Un расход.

∑Vn

расход.

∞

∑Un −

расход.

перехода:

n=1

m=1

∞

Замечание: В качестве рядов для сравнения

Замечание:

Un+1

< 1 ∑Un

сход., Un+1 > 1 ∑Un

расход.

∞

n=1

удобно выбирать ряды ∑

и ∑a qn

∫

f (x)dx = lim ∫ f (x)dx

n=1 n

n=0

n→∞

25. Знакопеременные числовые ряды

∞

∑Un = U1 +U2 +U3 + ...+Un '+..., Un - действительные числа

n=1

Определение

произвольного признака

∞

В частности, ∑(−1)n−1 n = U1 −U2 +U3 − ..., Un > 0, n -

n=1

знакочередующийся ряд

Абсолютная и

∞

1. ∑Un

и ∑

сходятся ∑Un - абсолютно сходится

условная

n=1

сходимость

∞

знакопеременных

2. ∑Un

сходится, а ∑

расходится

∑Un - условно сходится

рядов

n=1

Достаточные признаки сходимости знакопеременных рядов

Признак абсолютной

Признак Лейбница

сходимости

∞

∑Un - знакопеременный

1) U1 −U2

+U3 −... = ∑(−1)n−1 Un

∑(−1)n−1 Un

сходится

n=1

∞

2) U1 > U2

> U3

> ... > Un > ...

< U1

∑

сходится

∑Un

n=1

3) lim Un = 0

< U

n+1

абсолютно сходится

n→∞

Замечание:

1. В сходящемся знакочередующемся ряде U −U2 +U3 −...+ (−1)n−1 Un + (−1)nUn+1

+ ...

1444442444443

1442443

сумма S может быть заменена Sn (S ≈ Sn ). Получаемая погрешность Rn = S − Sn < Un+1

2. Убывание модулей членов знакопеременного ряда можно доказать с помощью

∞

производной. Если

'< 0 с некоторого номера, то члены ряда ∑

убывают с этого

n=1

номера.

∞

3. Если расходимость ряда ∑

установлена признаком Даламбера или признаком

n=1

∞

Un+1

Коши, то и ряд ∑Un

расходится, т. к. если lim

> 1 или lim n

> 1, то limUn ≠ 0 .

n=1

n→∞

∞

Алгоритм исследования знакопеременного ряда ∑Un на сходимость.

n=1

∞

1. Составить ряд из абсолютных членов данного ряда ∑

и исследовать его

n=1

сходимость.

∞

2. а) ∑

сходится ∑Un абсолютно сходится; б) ∑

расходится 3 исследуй

n=1

3. Проверить условия признака Лейбница

Если 1) члены чередуются по знаку;

> ...;

∞

3) lim

= 0 то 1) ∑Un

сходится по признаку Лейбница

n→∞

n=1

	∞		∞
2) ∑Un условно сходится, т. к. ∑				Un	расходится
2) ∑Un условно сходится, т. к. ∑				Un	расходится
	n=1		n=1
26. Функциональные ряды. Основные понятия

Понятие		Определение и обозначение
			∞
1. Функциональный ряд	U1(x) +U2(x) + ...+Un (x) + ... = ∑Un (x)
			n=1
2. Члены ряда	U1(x),U2(x),...,Un (x),... - функции от x

	∞		∞
3. Сходимость ряда в точке	∑Un (x0 )	сходится	∑Un (x) сходится в т. x0
3. Сходимость ряда в точке	n=1		n=1
x0	∞		∞
	∑Un (x0 )	расходится	∑Un (x) расходится в т. x0
	n=1		n=1
	∞
	∑Un (x) сходится x D D - область сходимости; D -

n=1

4.Область сходимости ряда находится:

Un+1(x)

l(x)

< 1,

lim

< 1 или lim n

(x)

n→∞

(x)

n→∞

5. Последовательность

S1(x), S2 (x),..., Sn (x),..., где

частичных сумм

Sn (x) = U1(x) +U2 (x) + ...+Un (x), n = 1,2,3...

6. Сумма сходящегося ряда

lim Sn (x) = S(x), x D S(x) - сумма ряда

n→∞

7. Остаток ряда

Rn (x) = S(x) − Sn (x)

8. Равномерная сходимость

∞

ε > 0 N(ε) : n ≥ N(ε) и x D

Rn (x)

< ε

ряда ∑Un (x) на D

n=1

9. Абсолютная и

Un (x)

≤ Un , n и x D

∞

равномерная сходимость

∞

∑Un (x) - сходится

n=1

ряда (признак

2. числовой ряд ∑Un

абсолютно и равномерно

Вейерштрасса)

n=1

сходится

на D

Свойства равномерно сходящихся рядов

∞

1. S(x) - непрерывна на D

1. ∑Un (x) = U1(x) +U2 (x) + ...+Un (x) + ...

2. ∫U1(x)dx + ...+ ∫Un (x)dx + ... = ∫S(x)dx , где

n=1

- равномерно сходится на D

[a,b] D (почленное интегрирование)

2. Un (x) - непрерывна n и x D

∞ x

∞

3. ∑∫Un

(x)dx - равномерно сходится на D ,

3. S(x) - его сумма S(x) = ∑Un (x)

n=1

n=1 a

где [a, x] D

∞

1. ∑Un (x) = U1(x) + ... + Un (x) + ... -

n=1

сходится на D , S(x) - его сумма

2.Un (x) - дифференцируемые n и x D

3.Un′ (x) - непрерывны n и x D

∞

1. ∑Un (x) - равномерно сходится на D

n=1

∞

2.∑Un′ (x) = U1′(x) + ...+ Un′ (x) + ... = S′(x) x D

n=1

(почленное дифференцирование)

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.11.2019190.46 Кб2Tx_3_Dec_Zan.doc
#
16.11.2019250.37 Кб5Tx_5_ Dec_Zan.doc
#
31.07.20192.3 Mб27TYeHNOLOGIChYeSKIJ_PROTsYeSS_PROIZVODSTVA_SLYaB....doc
#
20.11.20191.81 Mб299Uchebnoe_posobie_po_okhrane_truda.doc
#
11.02.2015778.78 Кб60Uchebnye_karty_Chast1.pdf
#
11.02.20151.24 Mб37Uchebnye_karty_Chast_2.pdf
#
27.11.2019482.3 Кб45UMK_GMU.doc
#
11.02.20156.48 Mб53Untitled.FR11.doc
#
16.12.2018149.5 Кб76upravlenie_personalom_kursovaya_rabota_2011.doc
#
21.08.2019307.71 Кб50Upravlenie_ZhKKh.doc
#
01.05.2025684.44 Кб4UP_Smazka_i_EGD_2_03_13.docx