
- •Тема1 Кинематика поступательного и вращательного движения
- •Тема 2 Динамика поступательного движения
- •Тема 3 Динамика вращательного движения
- •Тема 4 Работа. Энергия
- •Тема5 Законы сохранения в механике
- •Тема6 Электростатическое поле в вакууме
- •Тема7 Законы постоянного тока
- •Тема 8 Магнитостатика
- •Тема 9 Явление электромагнитной индукции
Тема1 Кинематика поступательного и вращательного движения
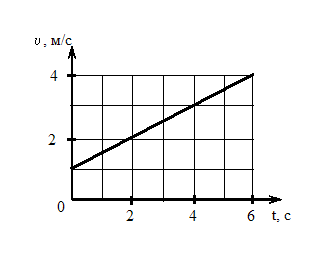
Твердое тело вращается вокруг неподвижной оси. Скорость точки, находящейся на расстоянии 10 см от оси, изменяется со временем в соответствии с графиком, представленным на рисунке.
 Угловое
ускорение тела (в единицах СИ) равно…
Угловое
ускорение тела (в единицах СИ) равно…
Решение:
По
определению угловое ускорение тела,
вращающегося вокруг неподвижной оси,
![]() ,
где
,
где![]() –
угловая скорость тела. Связь между
модулями угловой скорости вращения
тела и линейной скоростью точки, отстоящей
от оси вращения на расстояниеR,
имеет вид
–
угловая скорость тела. Связь между
модулями угловой скорости вращения
тела и линейной скоростью точки, отстоящей
от оси вращения на расстояниеR,
имеет вид
![]() .
Отсюда
.
Отсюда![]() ,
причемR
= 10 см
=
0,1 м.
Из представленного графика начальная
скорость
,
причемR
= 10 см
=
0,1 м.
Из представленного графика начальная
скорость
![]() м/с,
ускорение
м/с,
ускорение
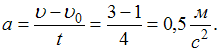 Итак,
зависимость скорости точки от времени
в единицах СИ задается уравнением
Итак,
зависимость скорости точки от времени
в единицах СИ задается уравнением![]() ,
а зависимость угловой скорости вращения
тела – уравнением
,
а зависимость угловой скорости вращения
тела – уравнением![]() .
Тогда
.
Тогда![]()
Диск вращается вокруг своей оси, изменяя проекцию угловой скорости
 так,
как показано на рисунке. Вектор угловой
скорости
так,
как показано на рисунке. Вектор угловой
скорости и
вектор углового ускорения
и
вектор углового ускорения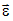 направлены
в одну сторону в интервалы времени …
направлены
в одну сторону в интервалы времени …
Решение:
По
определению угловое ускорение тела
![]() ,
где
,
где![]() –
его угловая скорость. При вращении
вокруг неподвижной оси векторы
–
его угловая скорость. При вращении
вокруг неподвижной оси векторы![]() и
и![]() коллинеарны,
причем направлены в одну и ту же сторону,
если вращение ускоренное, и в противоположные
стороны, если вращение замедленное.
Направление вектора
коллинеарны,
причем направлены в одну и ту же сторону,
если вращение ускоренное, и в противоположные
стороны, если вращение замедленное.
Направление вектора![]() связано
с направлением вращения тела правилом
правого винта. В интервале времени от
0 до
связано
с направлением вращения тела правилом
правого винта. В интервале времени от
0 до![]() вектор
угловой скорости направлен вдоль оси
OZ и, поскольку скорость увеличивается,
вектор углового ускорения направлен
так же. В интервале времени от
вектор
угловой скорости направлен вдоль оси
OZ и, поскольку скорость увеличивается,
вектор углового ускорения направлен
так же. В интервале времени от![]() до
до![]() вектор
угловой скорости направлен против оси
OZ, но скорость при этом также увеличивается,
следовательно, вектор углового ускорения
сонаправлен с вектором угловой скорости.
вектор
угловой скорости направлен против оси
OZ, но скорость при этом также увеличивается,
следовательно, вектор углового ускорения
сонаправлен с вектором угловой скорости.
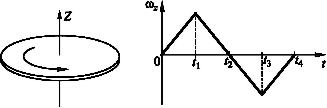
Диск равномерно вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. В некоторый момент времени к ободу диска была приложена сила, направленная по касательной.
 Решение:
Решение:
До остановки диска правильно изображает направление угловой скорости вектор …
Направление
вектора угловой скорости
![]() связано
с направлением вращения тела правилом
правого винта. В данном случае вектор
связано
с направлением вращения тела правилом
правого винта. В данном случае вектор![]() ориентирован
в направлении 4. После приложения силы
движение становится замедленным.
ориентирован
в направлении 4. После приложения силы
движение становится замедленным.
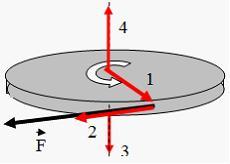
Точка М движется по спирали с равномерно убывающей скоростью в направлении, указанном стрелкой. При этом величина полного ускорения точки …
Решение:
Величина
полного ускорения определяется
соотношением
![]() ,
где
,
где![]() и
и![]() тангенциальное
и нормальное ускорения соответственно,
причем
тангенциальное
и нормальное ускорения соответственно,
причем![]() ,
,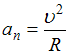 ,
гдеR
– радиус кривизны траектории. Так как
по условию скорость убывает равномерно,
величина тангенциального ускорения
остается постоянной. В то же время
величина нормального ускорения
уменьшается, поскольку при этом радиус
кривизны траектории увеличивается, что
видно из рисунка. Таким образом, полное
ускорение точки уменьшается.
,
гдеR
– радиус кривизны траектории. Так как
по условию скорость убывает равномерно,
величина тангенциального ускорения
остается постоянной. В то же время
величина нормального ускорения
уменьшается, поскольку при этом радиус
кривизны траектории увеличивается, что
видно из рисунка. Таким образом, полное
ускорение точки уменьшается.
Тема 2 Динамика поступательного движения
Автомобиль поднимается в гору по участку дуги с постоянной по величине скоростью.
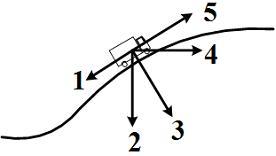 Равнодействующая
всех сил, действующих на автомобиль,
ориентирована в направлении …
Равнодействующая
всех сил, действующих на автомобиль,
ориентирована в направлении …
Решение:
Согласно
второму закону Ньютона
![]() ,
где
,
где![]() –
равнодействующая всех сил, действующих
на тело,
–
равнодействующая всех сил, действующих
на тело,![]() –
его ускорение. Вектор ускорения удобно
разложить на две составляющие:
–
его ускорение. Вектор ускорения удобно
разложить на две составляющие:![]() .
Тангенциальное ускорение
.
Тангенциальное ускорение
![]() направлено
по касательной к траектории в данной
точке и характеризует быстроту изменения
модуля скорости; нормальное ускорение
направлено
по касательной к траектории в данной
точке и характеризует быстроту изменения
модуля скорости; нормальное ускорение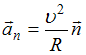 направлено
по нормали к траектории в данной точке
(направление 3) и характеризует быстроту
изменения направления скорости. При
движении по криволинейной траектории
направлено
по нормали к траектории в данной точке
(направление 3) и характеризует быстроту
изменения направления скорости. При
движении по криволинейной траектории![]() 0,
при движении с постоянной по величине
скоростью
0,
при движении с постоянной по величине
скоростью![]() 0.
Следовательно, вектор
0.
Следовательно, вектор![]() ориентирован
в направлении 3. В этом же направлении
ориентирован и вектор
ориентирован
в направлении 3. В этом же направлении
ориентирован и вектор
![]() .
.
Материальная точка движется под действием силы, изменяющейся по закону
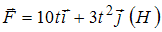 .
В момент времени
.
В момент времени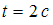 проекция
импульса (в
проекция
импульса (в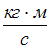 )
на ось ОХ равна …
)
на ось ОХ равна …
Решение:
Согласно
второму закону Ньютона, скорость
изменения импульса материальной точки
равна действующей на нее силе:
![]() .
В проекции на ось ОХ
.
В проекции на ось ОХ![]() .
Отсюда,
.
Отсюда,![]() следовательно,
следовательно,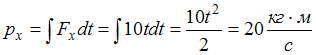
Механическая система состоит из трех частиц, массы которых
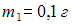 ,
,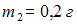 ,
,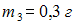 .
Первая частица находится в точке с
координатами (2, 3, 0), вторая – в
точке (2, 0, 1), третья – в точке
(1, 1, 0) (координаты даны в сантиметрах).
Тогда
.
Первая частица находится в точке с
координатами (2, 3, 0), вторая – в
точке (2, 0, 1), третья – в точке
(1, 1, 0) (координаты даны в сантиметрах).
Тогда –
координата центра масс (всм)
– равна …
–
координата центра масс (всм)
– равна …
Решение:
Центром
масс системы материальных точек
называется точка С, радиус-вектор которой
определяется соотношением
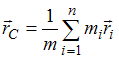 .Тогда
.Тогда
Импульс материальной точки изменяется по закону
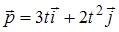 (кг·м/с).
Модуль силы (в Н),
действующей на точку в момент времени
t
= 1 c,
равен …
(кг·м/с).
Модуль силы (в Н),
действующей на точку в момент времени
t
= 1 c,
равен …
Решение:
Согласно
второму закону Ньютона скорость изменения
импульса материальной точки равна
действующей на нее силе:
![]() .
Тогда зависимость силы от времени имеет
вид
.
Тогда зависимость силы от времени имеет
вид![]() .
Модуль силы
.
Модуль силы![]() ,
и в момент времени t
= 1 c
,
и в момент времени t
= 1 c
![]()
