Коэффициент кинематической вязкости ν, коэффициент теплопроводности λ и критерий Прандтля Pr для воздуха и дымовых газов среднего состава(11% н2о и 13% со2)

Температура, 0С	Воздух			Дымовые газы среднего состава
	ν·106, м2/с	λ·102, вт/(м*град)	Pr	ν·106, м2/с	λ·102, вт/(м*град)	Pr
0	13,3	2,44	0,707	12,2	2,28	0,72
100	23,0	3,21	0,688	21,5	3,13	0,69
200	34,8	3,93	0,68	32,8	4,01	0,67
300	48,2	4,61	0,674	45,8	4,84	0,65
400	63,0	5,21	0,678	60,4	5,7	0,64
500	79,3	5,75	0,687	76,3	6,56	0,63
600	96,8	6,23	0,699	93,6	7,42	0,62

Продолжение таблицы 2.1

Температура, 0С	Воздух			Дымовые газы среднего состава
	ν·106, м2/с	λ·102, вт/(м*град)	Pr	ν·106, м2/с	λ·102, вт/(м*град)	Pr
700	115	6,71	0,706	112	8,27	0,61
800	135	7,18	0,713	132	9,15	0,60
900	155	7,63	0,717	152	10,01	0,59
1000	178	8,12	0,719	174	10,9	0,58
1100	199	8,47	0,722	197	11,75	0,57
1200	223	8,89	0,724	221	12,56	0,56
1300	-	-		245	13,49	0,55
1400	273	9,96		272	14,42	0,54
1500	-	-		297	15,35	0,53
1600	328	11,22		323	16,28	0,52

2.2. Динамический и тепловой пограничные слои

Для изучения турбулентного движения изложенный выше теоретический подход невозможен. По этой причине получают большое значение решения, основанные на теории пограничного слоя, основы которой были заложены Л. Прандтлем в 1904 г. применительно к гидродинамике.

В теории пограничного слоя предполагается, что можно выделить в потоке две области: внешний поток и тонкий пограничный динамический слой, внутри которого сильно проявляется вязкость, сказывающаяся в резком изменении скорости потока.

На рис.2.2 показана схема пограничного слоя хорошо обтекаемой пластины. Скорость ω₀ и температура t₀ набегающего потока постоянны. Предполагается безотрывное обтекание поверхности. Около поверхности скорость течения очень быстро падает до нуля вследствие действия сил вязкости. Жидкость как бы прилипает к поверхности, вследствие чего образуется тонкий динамический пограничный слой, в котором скорость изменяется от нуля на поверхности до скорости потока вдали от поверхности.

Из рис. 2.2 видно, что чем больше расстояние х от начала пластины, тем толще пограничный слой δ, так как по мере движения влияние вязкости распространяется все больше на невозмущенный поток. Строго говоря, изменение скорости в пределах пограничного слоя асимптотически приближается к скорости внешнего потока, и поэтому за толщину пограничного слоя принимают обычно такое ее значение, при котором скорость отличается от скорости внешнего потока на определенную, заранее принятую, величину (≈1%).

При увеличении скорости набегающего потока пограничный слой как бы сдувается и делается тоньше; наоборот, при увеличении вязкости, характеризуемой коэффициентом μ, толщина слоя увеличивается. При малых значениях х в пограничном слое происходит ламинарное течение. Но поскольку при увеличении

значения х толщина пограничного слоя увеличивается, движение в нем становится неустойчивым и переходит в турбулентное. Однако и в турбулентном пограничном слое можно выделить ламинарный вязкий подслой, в пределах которого скорость особо круто возрастает.

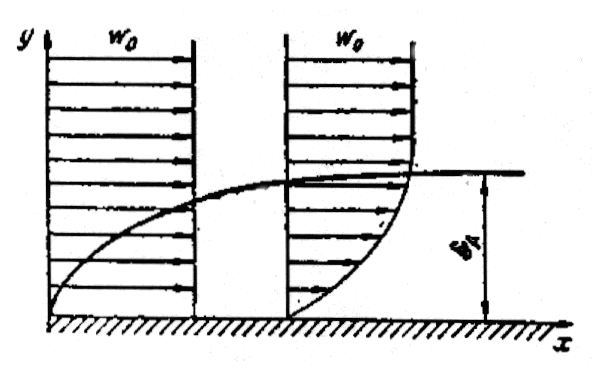
Рис.2.2.Изменение скоростей в гидродинамическом пограничном слое

Толщина пограничного слоя зависит от формы и размеров теплоотдающей поверхности, так как при изменении формы и размеров ее изменяется и характер обтекания. Следовательно, будет изменяться и интенсивность теплоотдачи.

Изменение температуры потока показано на рис. 2.3; она сильно изменяется от значения t_с - температуры стенки до t₀ – температуры внешнего потока.

Рис.2.3.Изменение температур в тепловом пограничном слое

Г.Н. Кружилиным, по аналогии с динамическим пограничным слоем, было введено понятие теплового пограничного слоя, в пределах которого изменяется температура от t_с до t₀.

Толщина теплового слоя отличается от толщины динамического слоя и их соотношение определяется величиной δ_т/δ≈1/, но для газов и горячей воды эти толщины практически совпадают, так

как критерий Pr близок к единице.

У поверхности тепло проходит только вследствие теплопроводности, т.е. в данном случае можно применить закон Фурье

q = -λ (∂t / ∂n)_n-0,

где λ – коэффициент теплопроводности теплоносителя;

n – нормаль к поверхности нагрева;

∂t / ∂n – градиент температуры движущейся среды у поверхности нагрева.

В слое толщиной δ_т температура среды резко изменяется от t_с до t_окр.

Температурный градиент у поверхности стенки можно приблизительно выразить уравнением

(∂t/∂n)≈-(t_окр-t_с)/δ_т=-∆t/δ_т. (2.5)

Величина теплового потока определяется формулой Ньютона-Рихмана

. (2.6)

Из-за трудности определения величины λ/δ_т пользуются формулой конвективного теплообмена

q=α(t_окр-t_с)=α∆t. (2.7)

Таким образом, коэффициент конвективной теплоотдачи можно определить из сравнения уравнений (2.5), (2.7)

α=-λ/∆t·(∂t/∂n)≈λ/δ_т . (2.8)

Пример 2.1. Оценить приблизительно толщину теплового пограничного слоя при движении воздуха со скоростью 16 м/с внутри трубы диаметром 60 мм, если известно, что при этом коэффициент теплоотдачи составляет α = 56 ,Вт/(м² град), а коэффициент теплопроводности воздуха λ = 2,5 * 10^-2 Вт/(м град). Толщина пограничного слоя составит

δ_т ≈ λ/α = 2,5·10^-2 /56 = 463·10^-6 м = 0,46 мм.

Толщина пограничного слоя обратно пропорциональна критерию Рейнольдса Re = ωd/ν. Для данного канала и текущей среды чем больше скорость (вдали от стенки) газа, тем меньше толщина пограничного слоя. Поэтому для интенсификации теплоотдачи принимают повышенные скорости и стараются турбулизировать поток, применяя те или другие технические приемы. Поверхностям нагрева придают форму, обеспечивающую завихрение потока теплоносителя или вызывающую его прерывистость. Это касается, в первую очередь, газообразных теплоносителей, у которых коэффициенты теплоотдачи невелики.

Из формулы (2.8) видно, что коэффициент конвективной теплоотдачи α зависит от толщины пограничного слоя δ_т (определяемый характером движения теплоносителя, величиной скорости, приведенным диаметром канала и свойствами движущей среды – коэффициентом кинематической вязкости ν и коэффициентом теплопроводности λ).

Коэффициент конвективной теплоотдачи α тем больше, чем меньше коэффициент теплопроводности λ и скорость потока ω, чем меньше коэффициент динамической вязкости μ и больше плотность ρ, т.е. чем меньше коэффициент кинематической вязкости ν = μ/ρ и чем меньше приведенный диаметр канала d. В дальнейшем будет показано, что на величину α влияют также теплоемкость жидкости с, температуры жидкости t_окр и стенки канала t_с, а также другие факторы (форма поверхности Ф, размеры поверхности l₁, l₂, l₃ и др.). Таким образом

α=ƒ(ω,λ,с,ρ, μ, t_окр, t_с, Ф, l₁, l₂ …). (2.9)

Из-за большого числа переменных очень трудно вывести формулы для расчета коэффициентов теплоотдачи математическим путем. Теория пограничного слоя оказалась весьма плодотворной и, пользуясь ей, можно дать приближенные аналитические решения, которые дают хорошую сходимость с практикой. Но чаще всего значения коэффициентов теплоотдачи определяют по экспериментальным формулам. Однако непосредственные опытные исследования без научно-теоретического обоснования потребовали бы проведения огромного количества экспериментальных работ, так как для каждого конкретного (единичного) влияния необходимо было бы осуществлять самостоятельное изучение.