1.2. Дифференциальное уравнение распространения тепла

Для изучения закономерностей распространения тепла в однородном и изотропном теле составим уравнение, описывающее изменение температуры в любой точке нагреваемого тела в зависимости от времени. Коэффициент теплопроводности и другие физические характеристики будем считать постоянными и допустим, что деформацией тела от изменения температуры можно пренебречь. В объеме тела могут действовать внутренние источники тепловыделения (например, при нагреве тела путем пропускания электрического тока), но эти источники распределены равномерно.

При выводе дифференциального уравнения применим закон сохранения энергии, сочетая его с основным законом теплопроводности. Выделим в теле элементарный параллелепипед с гранями dx, dy, dz (рис. 1.3).

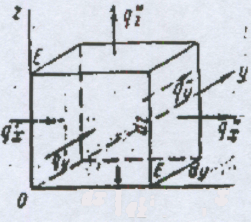
Рис. 1.3. К выводу дифференциального уравнения

теплопроводности

Количество поступившей теплоты и выделенной внутренними источниками dq_BH, за вычетом количества теплоты, уходящей через поверхность наружу dq_yx, идет на приращение внутренней энергии вещества в выделенном объеме

du=dq-dq_yx. (1.7)

Если объемная мощность тепловыделения q_v Вт/м³, то за время d выделится тепла

dq_BM=q_vdxdydzd. (1.8)

По закону Фурье количество тепла, проходящее за время d через грань dydz вдоль оси х, равно

dq_x'=-()dydzd. (1.9)

Плотность теплового потока, проходящая через противоположную грань dydz, температура которой t+()dx, будет

dq_x"=-(д/дх)·(t+(дt/дх)dx)dydzd. (1.10)

Разность величин этих потоков

dq_x'-dq_x"=-()dxdydzd. (1.11)

Рассуждая аналогично для направлений теплового потока по осям у и z, получим:

dq_y'-dq_y"=-()dxdydzd; (1.12)

dq_z'-dq_z"=-()dxdydzd. (1.13)

Общее количество тепла, оставшегося в элементе в единицу времени, равно сумме выражений (1.11), (1.13)

dq=(++)

dxdydzd. (1.14)

Масса элемента при плотности вещества , кг/м³ , будет равна dxdydz.

Внутренняя энергия элемента изменится на величину

du=-c(dxdydzd, (1.15) здесь с — средняя теплоемкость вещества элемента, Дж/(кг·град).

Приравнивая выражения (1.14) и (1.15), получим

(=q_v+(++). ( 1.16)

или

=a(++)+q_v/c=а▼²t. (1.17)

Мы ввели новую физическую характеристику а = /с, м²/с, называемую коэффициентом температуропроводности; выражение ▼²t=d²t/dx²+d²t/dy²+d²t/dz² называют оператором Лапласа.

Выражение (1.17) называют дифференциальным уравнением теплопроводности Фурье.

Наиболее просто это уравнение выглядит для случая распространения тепла для плоской стенки (для пластины неограниченного размера), когда тепло распространяется только в направлении оси х и когда отсутствуют внутренние источники тепла, т.е. при q_v = 0.

=a(). (1.18)

Чем больше коэффициент температуропроводности

а = /с, тем пропорционально быстрее распространяется температура в теле, т.е. оно быстрее нагревается или охлаждается. Стало быть на этот процесс влияют три параметра:, с и, и из них с идействуют обратно пропорционально. Дифференциальное уравнение теплопроводности позволяет решать многие практические задачи, однако решения получаются не всегда простыми.