3.2. Частные производные и градиент

Пусть - функция двух переменных. Первая производная функциипо переменнойпри фиксированной переменнойназывается (первой) частной производной функциипо переменной, символически записывают так:

или, или, или.

Аналогично определяется (первая) частная производная функции по переменной:

или, или, или.

При нахождении частной производной надо считать постоянной переменную. При этом сохраняются все известные правила дифференцирования.

Пример 20. Найти частные производные:

а) ; б).

Решение

а)

.

.

б) При фиксированном имеем показательную функцию

.

При фиксированном имеем степенную функцию

.

Упорядоченная пара частных производных илифункциидвух переменных обозначается символомилии называется градиентом функциидвух переменных. Градиент функции двух переменных естьдвумерный вектор.

Градиент функциив точкепоказывает направление самого быстрого роста функциив точке.

Пример 21. Для функции двух переменных:

а) построить линию уровня, проходящую через точку (1; 9);

б) найти градиент в этой точке;

в) построить градиент.

Решение

а) Найдём уровень , который равен частному значению функциив точке (1; 9):.

Уравнение линии уровня имеет вид

или, или, или- гипербола (рис. 5).

б) Найдём

,,

,,

.

в) Строим вектор выходящим из точки. Конец вектора в точкес координатами

,.

Рис. 5

Градиент всегда перпендикулярен линии уровня, проходящей через точку.

3.3. Частные производные высших порядков

Пусть определена на множествеи в каждой точкесуществуют (первые) частные производныеи. Первые частные производные представляют собой новые функции двух переменных. Частные производные от функцийиназываются частными производными второго порядка (или вторыми частными производными) от функции.

Таким образом, имеем четыре вторых частных производных, которые обозначаются:

или

.

Частные производные второго порядка иназываются смешанными частными производными. Если смешанные частные производные непрерывны, то они обязательно равны.

Пример 22. Найти все частные производные второго порядка от функции.

Решение

3.4. Экстремум функции двух переменных

Локальный экстремум

Окрестностью точки называется круг, содержащий точку.

Точка называется точкой локального максимума (минимума) функции, если существует окрестность точки, в которой для любой точкивыполняется неравенство

.

Точки локального максимума и локального минимума называются точками локального экстремума.

Необходимое условие локального экстремума формулируется следующим образом.

Если функция имеет частные производные первого порядка в точке локального экстремума, то

.

Итак, «подозрительными» на экстремум являются те точки , в которых все частные производные первого порядка обращаются в нуль. Такие точки называются стационарными.

Сформулируем достаточные условия экстремума функции двух переменных.

Пусть функция имеет непрерывные частные производные второго порядка в некоторой окрестности стационарной точки.

Положим .

Тогда:

1) если , то в точкефункция имеет локальный экстремум, причём при- локальный максимум, при- локальный минимум;

2) если , то в точкенет экстремума;

3) если , то вопрос о наличии экстремума остаётся открытым.

Пример 23. Функция полных издержек двух продуктовых фирм задана уравнением, гдеи- объёмы выпуска товаровисоответственно. Цены этих товаров на рынке равны 8 и 6. Определить максимально возможное значение прибыли.

Решение

Найдём значение прибыли от реализации товара ив объёмахикак разность между доходом от продажии издержками.

.

Определим стационарные точки функции. Найдём частные производные:

,.

Решим систему:

Точка - стационарная точка функции.

Найдём частные производные второго порядка:

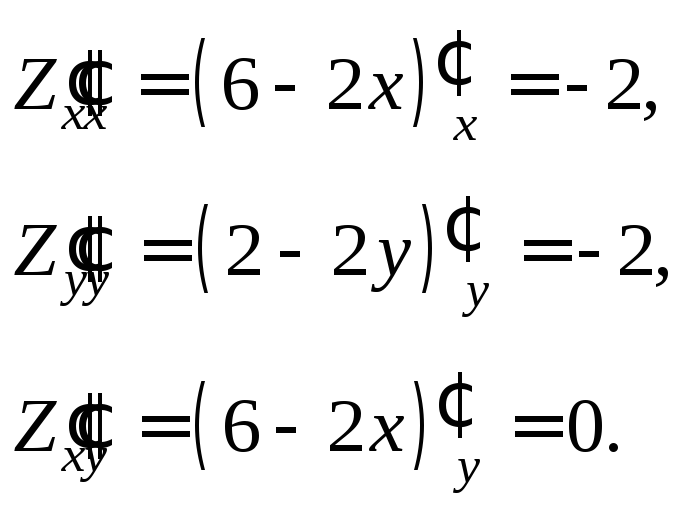
Учитывая что , а, определим:- точка максимума. Найдём максимальное значение прибыли.

Условный экстремум

Экстремум функции при условии, чтоисвязаны уравнением, называется условным экстремумом. Уравнениеназывается уравнением связи.

Для решения задач на условный экстремум обычно используется метод Лагранжа.

Составим вспомогательную функцию

.

Функция называется функцией Лагранжа, а- множителем Лагранжа.

Точка условного экстремума является точкой локального экстремума функции Лагранжа , её координаты должны удовлетворять уравнениям

Пусть - любое решение этой системы и

.

Если , то функцияимеет в точкеусловный максимум, если, то условный минимум.

Пример 24. Найти экстремумпри условии.

Решение

Функция Лагранжа имеет вид .

Найдём частные производные

.

Решим систему

- «подозрительная» точка.

Наёдем частные производные

Вычислим определитель

.

В точке функцияимеет условный экстремум

.