2.2. Основные свойства определённого интеграла

По определению.

По определению.

Каковы бы ни были числа, всегда имеет место равенство.

Постоянный множитель можно выносить за знак определён­ного интеграла, т.е..

Определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов

.

Пример 10. Вычислить интеграл.

Решение

.

Интеграл от неотрицательной функции на отрезке- неотрицательное число, то есть еслина, то.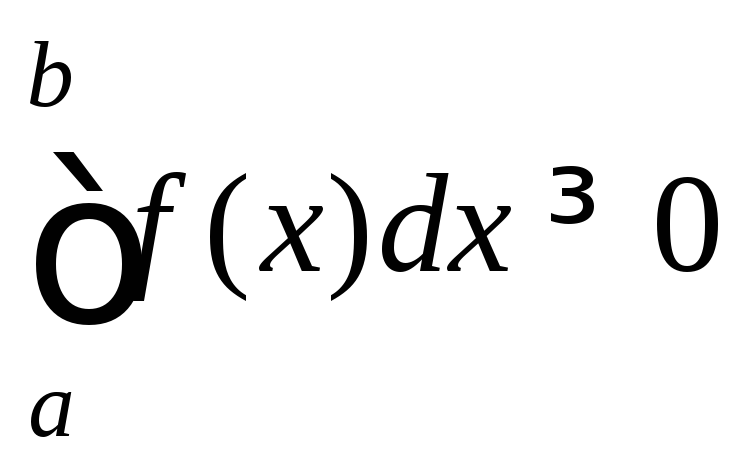

Если навыполняется неравенство, то такое же неравенство выполняется и для интегралов, т.е.

.

Пусть- наименьшее, а- наибольшее значения непре­рывной функциина, тогда

.

Пример 11. Оценить определённый интеграл.

Решение

Функция убывает на промежутке, поэтому,. Значит,.

Еслинепрерывна на отрезке, то найдётся такое значение, что.

- среднее значение функциина отрезке.

При вычислении определённых интегралов применяют также метод замены переменной, который позволяет упростить интеграл. При этом в отличие от неопределённого интеграла нет необходимости возвращаться к исходной переменной интегрирования. Достаточно найти пределы интегрирования новой переменной и воспользоваться формулой Ньютона-Лейбница.

Формула замены переменной в определённом интеграле имеет вид

.

Пример 12. Вычислить интегралы:

а) ; б).

Решение

а)

.

б)

.

Формула интегрирования по частям в определённом интеграле имеет вид

.

Пример 13. Вычислить интеграл.

Решение

,

так как ,.

2.3. Приложения определённого интеграла

Вычисление площадей плоских фигур. Пусть функциянепрерывна и неотрицательна на отрезке. Тогда пло­щадьпод кривойначисленно равна определённому интегралу, то есть

.

Пример 14. Найти площадь фигуры (рис.1), ограниченной ли­ниями,,,.

Рис. 1

Решение

Фигура заключена между графиками функций и. Площадьнаходим как разность площадей

.

Вычисление объёма тела вращения. Пусть- непре­рывна и неотрицательна на(рис.2). Тогда тело, образованное враще­нием вокруг осикриволинейной трапеции, имеет объём

.

Рис. 2

Пример 15. Найти объём тела (рис.3), полученного от вращения фигуры, ограниченной линиями,,,.

Рис. 3

Решение

Искомый объём равен

.

Экономические приложения определённого интеграла

Пример 16. Дана функция предельных издержек

,,

где - объём выпускаемого товара. Найти функцию издержек

и вычислить издержки в случае производства 10 единиц товара, если известно, что издержки для производства первой единицы товара составили 30 рублей.

Решение

Известно, что предельные издержки есть производная от функции издержек, т.е.. Значит, функцию издержек находим интегрированием

.

Для заданной функции имеем

или

.

Из условия найдём. Тогда получаем,

.

При вычислим.

Пример 17. Функция изменения затрат времени на изготовление изделий имеет вид. Найти среднее время, затраченное на освоение одного изделия в период освоения отдо.

Решение

Если известна функция , описывающая изменение затрат времени на изготовление изделия в зависимости от степени освоения производства, где- порядковый номер изделия в партии, то среднее время, затраченное на изготовление одного изделия в период освоения отдо, вычисляется с помощью интеграла

.

В нашем случае

.