МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Г.И. НОСОВА

КАФЕДРА МАТЕМАТИЧЕСКИХ МЕТОДОВ В ЭКОНОМИКЕ

ИНТЕГРАЛЫ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Методические указания к работе №2 для студентов заочной формы обучения экономических специальностей

Магнитогорск

2008

Составители: О.С. Андросенко,

Т.Г. Кузина

Интегралы. Функции нескольких переменных. Дифференциальные уравнения: Методические указания к работе №2 для студентов заочной формы обучения специальностей. Магнитогорск: МГТУ, 2008. 51 с.

Рецензент: Т.В. Морозова

© Андросенко О.С., Кузина Т.Г., 2008

1. Неопределённый интеграл и его свойства

1.1. Первообразная и неопределённый интеграл

В дифференциальном исчислении решается задача: по данной функции найти её производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию, зная её производную(или дифференциал). С такой задачей мы встречаемся и в экономике, например, при нахождении функции оборотных средств по известной скорости формирования оборотных средств.

Функция называетсяпервообразнойдля функциина интервале, если для любоговыполняется равенство

.

Например, первообразной функции , является функция, действительно. Первообразными будут также функции(- постоянная), которые также удовлетворяют условию .

Если первообразная для, то выражение, где- произвольная постоянная, называетсянеопределённым интеграломот функциии обозначается символом, где- подынтегральная функция,- подынтегральное выражение,- переменная интегрирования.

Таким образом,

.

Например, .

Нахождение первообразной по её производной или отыскание неопределённого интеграла по данной подынтегральной функции называется интегрированиемданной функции. Интегрирование – операция, обратная дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, надо взять производную от полученного результата и убедиться, что получена подынтегральная функция.

1.2. Свойства неопределённого интеграла. Таблица основных интегралов. Приёмы непосредственного интегрирования

Производная от неопределённого интеграла равна подынте­гральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению, т.е.

;.

Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная, т.е.

.

Постоянный множитель можно вынести из под знака неопреде­лённого интеграла, т.е.

.

Неопределённый интеграл от алгебраической суммы функций равен сумме интегралов от слагаемых, т.е.

.

Приведём таблицу основных интегралов

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

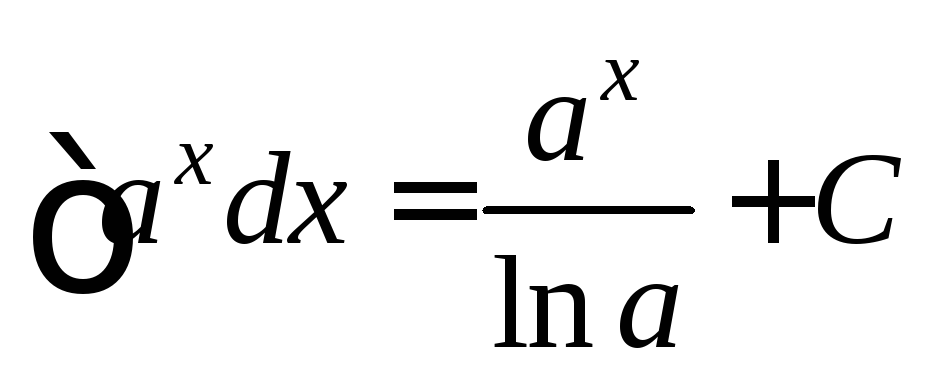Справедливость формул проверяется дифференцированием.

Вычисление интегралов с помощью таблицы основных интегралов и простейших приёмов называется непосредственным интегрирова­нием.

Пример 1. Найти.

Решение

Применив свойства и, имеем

=

= .

Далее находим интегралы с использованием табличных формул:

;

;

;

.

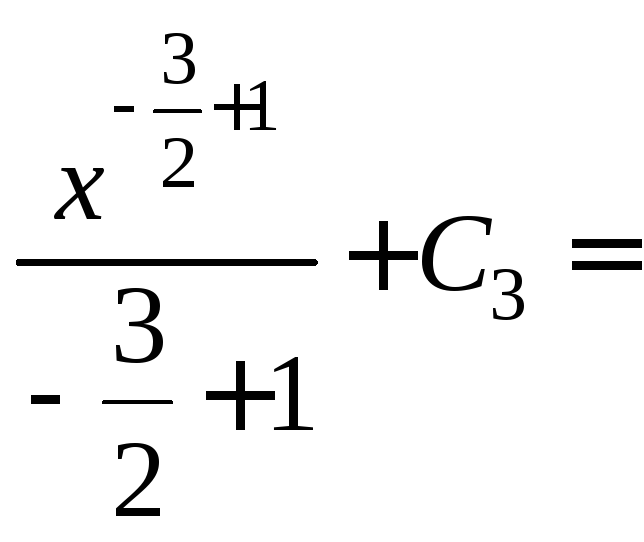
Таким образом,

=++

+.

Обычно, все произвольные постоянные суммируют, результат обозначают одной буквой, поэтому

=++

+.

Пример 2. Найти интегралы, разложив подынтегральную функ­цию в сумму функций:

а) ;

б) ;

в) .

Решение

а) Применяя формулу сокращенного умножения и умножая почленно, преобразуем подынтегральную функцию в сумму:

.

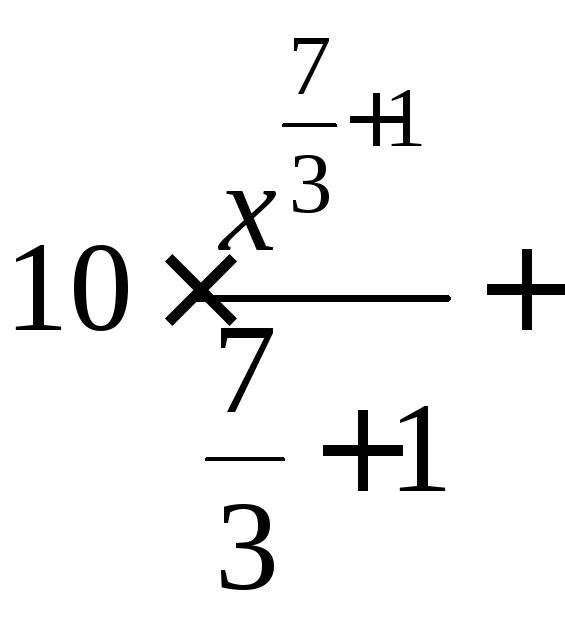
б) Разделим почленночислитель на знаменатель, применим свойства,и табличные интегралыIII,IV.

.

в) Для разложения подынтегральной функции в сумму функций разделимчислитель на знаменатель «углом».

Следовательно, , тогда

.

1.3. Интегрирование методом замены переменной

Метод замены переменной (или метод подстановки) позволяет упростить подынтегральное выражение и свести интеграл к линейной комбинации табличных интегралов. Метод основан на применении следующей формулы:

,

где - непрерывно дифференцируемая функция на рассматри­ваемом промежутке.

Пример 3. Найти интегралы:

а) ; б); в); г).

Решение

а) Чтобы избавиться от иррациональности, выполним замену переменной .

.

Возвращаясь к , получим

.

б)

.

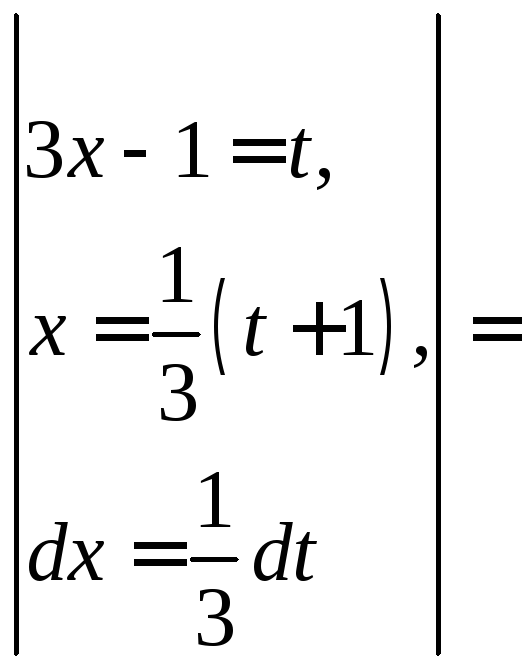
в)

.

г)

.

При вычислении интегралов б, в, г была использована линейная подстановка . В общем случае справедлива формула

,

Формулу применяют также в обратном направлении

.

В этом случае говорят о наличии дифференциальной связи.

Пример 4. Найти интегралы, используя наличие дифференциаль­ной связи:

а) ; б); в); г).

Решение

а)

.

б)

.

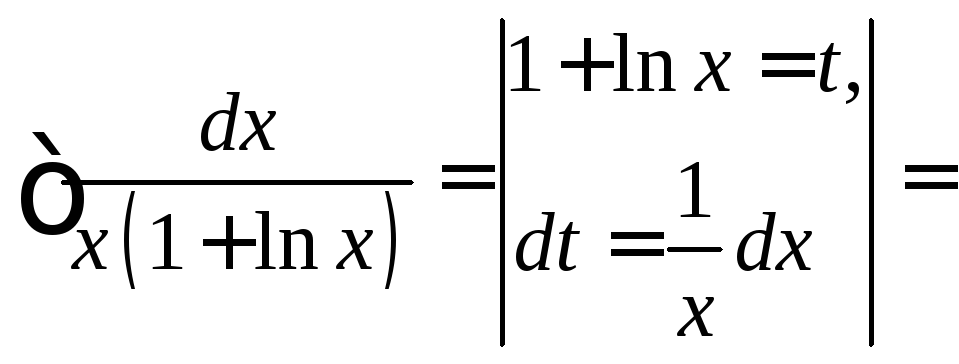
в)

.

г) .

В первом из интегралов выполним замену

.

,

значит

.