Классификация дифференциальных уравнений.
-
Дифференциальные уравнения первого порядка с разделяющимися переменными – уравнения следующего вида:
,
где
и
- заданные функции,
.
Эти уравнения приводятся к виду
,
где
,
при
.
Общий интеграл уравнения
имеет вид
.
Пример. Решить дифференциальное
уравнение
Разделим переменные
,
;
Проинтегрируем уравнение с последующим выражением искомой величины y из равенства:
;
;
- общее решение дифференциального
уравнения.
2. Однородные дифференциальные уравнения первого порядка – это уравнения вида:
,
где функция
обладает следующим свойством: равенство
выполняется для произвольного числа
>0.
Для решения однородного дифференциального
уравнения
необходимо:
1) свести его к уравнению вида
;
2) полученное уравнение свести к
уравнению с разделяющимися переменными,
используя новую переменную
3. Линейные дифференциальные уравнения первого порядка – это уравнения вида:
,
(*)
где
,
функции р(х) и f(х)
непрерывны на
,
причём
.
Решаются двумя способами. 1) Метод
Бернулли. Искомая функция
у(х)представляется в виде у=uv,
откуда, в силу
,
следует два уравнения для нахождения
функций u(x)
и v(x):
.
Из первого уравнения получаем
.
Из второго уравнения следует
,
откуда
,
и, таким образом, общее решение уравнения
(*) имеет следующий вид:
.
2) Метод вариации произвольной постоянной
(метод Лагранжа) также состоит из двух
этапов. На первом этапе решения уравнения
(*) находим общее решение уравнения
:
,
где С – произвольная постоянная. На
втором этапе ищем общее решение уравнения
(*) в виде
,
где С – функция от х. После подстановки
этого соотношения в уравнение (*) приходим
к уравнению
,
откуда следует
,
где А – произвольная постоянная, и
- общее решение уравнения (*).
Пример. Решить дифференциальное
уравнение
Воспользуемся подстановкой
(1)
Пусть
,
тогда уравнение (1) принимает вид системы:
Решим уравнение
как уравнение с разделяющимися переменными
;
;
;
- частное решение.
Подставляем последнее равенство в
и решим его относительно величины u:
;
;
;
Найдем искомую величину y,
подставив значения u
и v в формулу
-
общее решение дифференциального
уравнения.
Пример. Найти частное решение
уравнения
,
если
при
.
Разделив все члены данного уравнения
на
получим уравнение
(*)
которое является линейным. Положим
тогда
.
Подставив выражения для
и
в уравнение (*), имеем
или
(**)
Для отыскания u получаем уравнение
т.е.
,
откуда
Подставляя выражения для u в уравнение (*), имеем
,
или
т.е.
Следовательно, общее решение данного уравнения записывается так:
Используя начальные условия
,
имеем
откуда С=1. Таким образом, искомое частное
решение имеет вид
.
4. Уравнение Бернулли – это уравнение вида:
,
где
(при
- линейное дифференциальное уравнение,
при
- уравнение с разделяющимися переменными).
Уравнение приводится к линейному
дифференциальному уравнению с помощи
подстановки
(при
может быть потеряно решение
).
Поэтому оно решается как линейное: либо
методом Бернулли, либо методом Лагранжа.
Пример. Решить дифференциальное
уравнение
Введем замену z= y1-2
,
,
.
Подставим эти выражения в уравнение.
Получим
,
,
Решим полученное линейное уравнение методом Лагранжа.
,
,
,
,
.
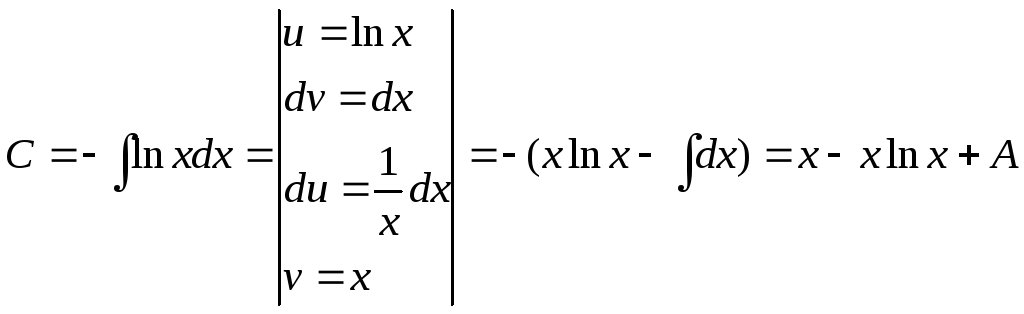
5.Простейшие дифференциальные уравнения n – го порядка, допускающие понижение порядка методом интегрирования обеих частей уравнения – это уравнения вида:
,
где
,
функции
(х)
и f(х) непрерывны
на
.
Пример. Решить уравнение
Уравнение является простейшим дифференциальным уравнением 2-го порядка. Понизим порядок уравнения методом интегрирования обеих частей уравнения
,
=
x + 3tgx + C 1, y
= ∫(x + 3tgx + C 1)dx
y = x 2 – 3ln׀cosx׀ + C1x + C2 – общее решение дифференциального уравнения
6. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами – это уравнения вида:
,
где
-
постоянные коэффициенты,
Метод решения. Составляют характеристическое уравнение
,
которое получается из дифференциального
уравнения заменой в нем производных
искомой функции y
соответствующими степенями r,
причем сама функция у заменяется
единицей.
Тогда общее решение дифференциального уравнения составляется в зависимости от дискриминанта D характеристического уравнения.
Рассмотрим следующие случаи:
а) D>0; два различных
действительных корня
;
тогда
- общее решение дифференциального
уравнения;
б) D=0; два равных
действительных корня
;
тогда
- общее решение дифференциального
уравнения;
в) D<0; два различных
комплексных корня:
,
где
,
-
действительные числа, причем
>0.
Тогда
- общее решение дифференциального
уравнения.
Пример. Найти частное решение
уравнения
,
удовлетворяющее начальным условиям
у(0)=0,
Данная задача с начальными условиями
носит название задачи Коши. Составим
характеристическое уравнение: r2-1=0.
Его решениями являются
Общее решение уравнения в этом случае
(Д>0) находится по формуле
,
т.е.
-
общее решение.
Найдем
Подставим в уравнения начальные условия:
Решая эту систему, получаем
Найденные значения постоянных с1
и с2 подставляем в общее решение
и получаем искомое решение
или
