Дифференциальные уравнения Основные понятия

При анализе динамических процессов в различных областях науки и техники часто возникают задачи решения дифференциальных уравнений, которые связывают искомую функцию и её производные различных порядков. Различают обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных.

Дифференциальное уравнение называется обыкновенным, если оно содержит искомую функцию от одной переменной, её производные различных порядков и независимую переменную. Общий вид обыкновенного дифференциального уравнения определяется следующим выражением: Если в уравнении искомая функция зависит от нескольких переменных и это уравнение содержит частные производные, то такое уравнение называется дифференциальным уравнением в частных производных. Порядком дифференциального уравнения называется порядок наивысшей производной, входящих в уравнение.

Пример. Задача нахождения первообразной - функции, производная которой при каждом значении равна заданной функции , - может быть записана как простейшее обыкновенное дифференциальное уравнение первого порядка: .

Любая функция , обращающая уравнение при в тождество, может быть выражена с использованием неопределенного интеграла . Здесь и далее - какая-либо одна из первообразных функции , С – произвольная постоянная.

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида _{, где F – функция от трех переменных.}

_{Уравнение} , где - функция, определённая в некоторой области D плоскости Оху, называют дифференциальным уравнением первого порядка, разрешенным относительно производной. Предполагается, что функция является непрерывной.

Решением дифференциального уравнения на некотором интервале называется функция , определенная и дифференцируемая на этом интервале и удовлетворяющая следующим двум условиям:

1. точка 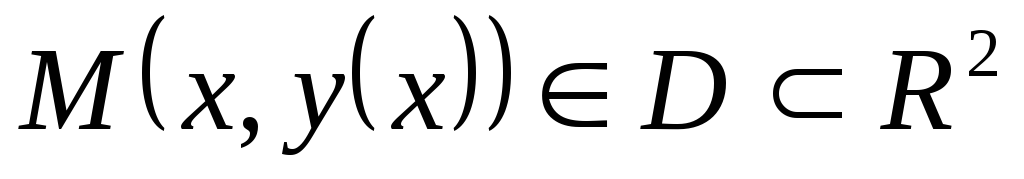при любом ;

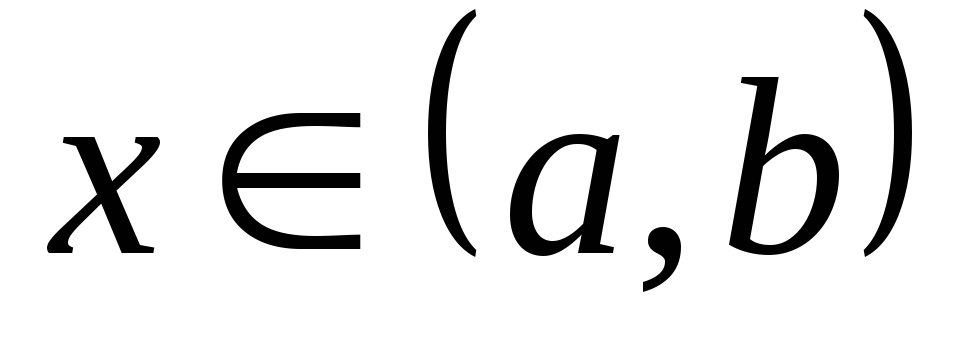2. при любом .

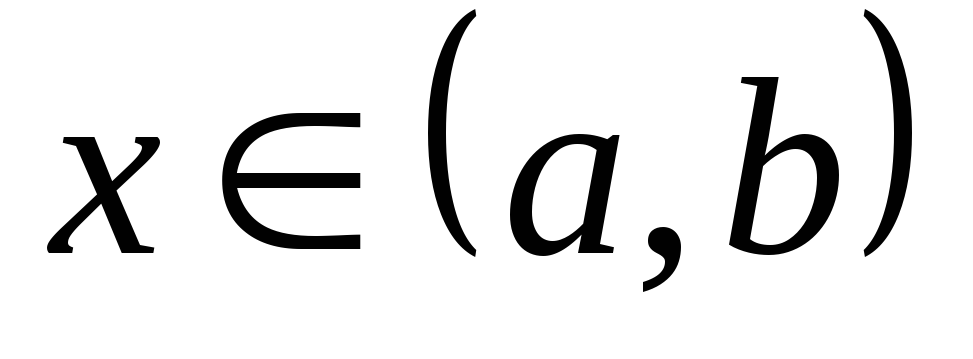Решить (проинтегрировать) дифференциальное уравнение-

значит, найти все его решения в заданном конечном или бесконечном интервале .

Интеграл дифференциального уравнения - решение этого уравнения, заданное в неявном виде.

График решения дифференциального уравнения на плоскости Оху называется интегральной кривой.

Задача Коши при решении дифференциального уравнения заключается в следующем: требуется найти его решение, удовлетворяющее начальному условию , где .

Пусть задано дифференциальное уравнение . Если функция и её частная производная определены и непрерывны в некоторой области D, и точка ,то существует единственное решение уравнения , удовлетворяющее начальному условию .

Общим решением дифференциального уравнения в некоторой области называется функция ,зависящая от переменной х и одной произвольной постоянной С (параметра), если:

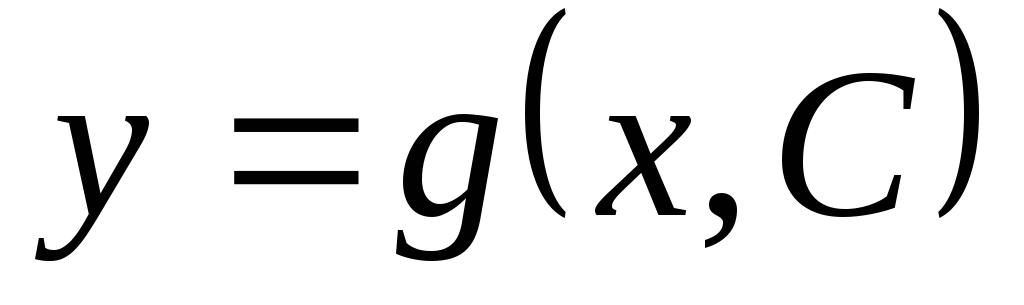1. является решением уравнения при любом допустимом значении постоянной С;

2. при любом начальном условии , удовлетворяющем условию 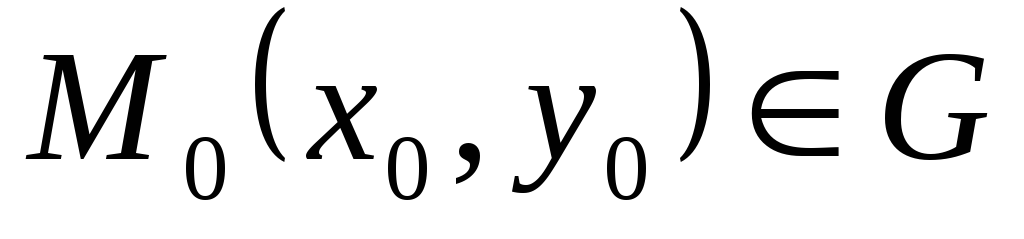, существует единственное значение параметра 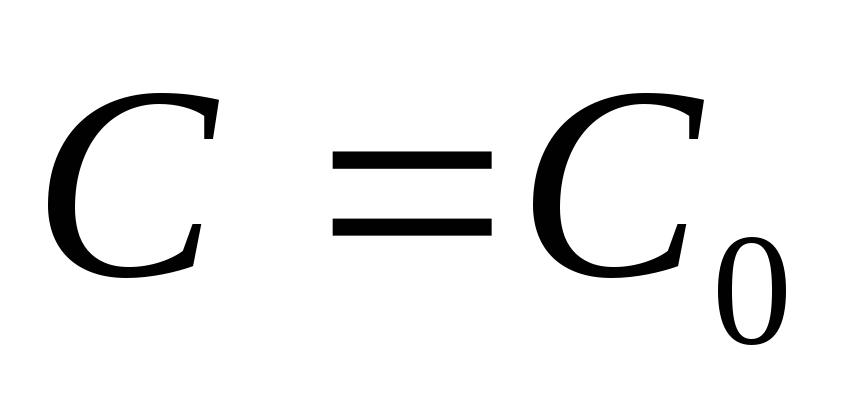такое, что функция удовлетворяет условию .

Частным решением дифференциального уравнения в некоторой области называется функция , которая получается из общего решения уравнения в области G при конкретном значении произвольной постоянной .