- •II.Элементы функционального и комплексного анализа.
- •Решение задачи:
- •6. Формула включений и исключений.
- •Упражнения и задачи по теории множеств
- •III. Введение в математический анализ. Дифференциальное исчисление функции.
- •Тема 1. Введение в математический анализ. Область определения функции совпадает с одз (областью допустимых значений) правой части, т.Е. С множеством всех значений х, при которыхвычисляется.
- •Вопросы для самопроверки:
- •Тема 2. Пределы
- •Вопросы для самопроверки:
- •Тема 3. Дифференциальное исчисление
- •Вопросы для самопроверки:
- •Тема 4. Приложения дифференциального исчисления
- •Вопросы для самопроверки:
- •Тема 5. Функции нескольких переменных
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •IV. Интегральное исчисление функции одной переменной.
- •Тема 1. Неопределенный интеграл
- •Вопросы для самопроверки.
- •Тема 6. Определенный интеграл
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •V. Дифференциальные уравнения.
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •VI. Числовые и функциональные ряды. Числовые ряды
- •Функциональные ряды
- •VII. Элементы теории вероятностей. Случайные события
- •Вопросы для самопроверки:
Самостоятельная работа студентов.
Элементы линейной алгебры и аналитической геометрии.
Пример 1. Действия с матрицами
Вычислим матрицу
2A-BA,
где
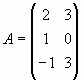 и
и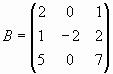 .
.
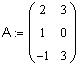

![]()
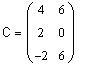
Вычислим матрицу D=BA размерности 3 x 2:
![]()

Вычислим матрицу 2A-BA размерности 3 x 2, равную матрице C-D:
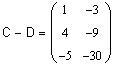
|
Пример
1.
Пусть
и
|
***
|
Пример 2. Матричное уравнение
определяет систему двух линейных уравнений с тремя неизвестными:
Коэффициенты при неизвестных пронумерованы двумя индексами, первый из которых можно интерпретировать как номер уравнения, а второй – как номер соответствующей переменной. |
Пример 3.
Вычислим
произведения AB
и BA
матрицы-строки
![]() и
матрицы-столбца
и
матрицы-столбца :
:
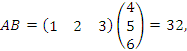

|
Пример 4. Пусть A, B и C – квадратные матрицы одного и того же порядка. Если существуют обратные матрицы A –1, B –1 и C –1, то существует и обратная матрица для произведения ABC, причем (ABC)–1 = C –1 B –1 A –1. Действительно,
Аналогично,
|
***
|
Пример
5.
Пусть
является обратной матрицей. Решение Вычислим произведение A –1A :
Такой же результат справедлив для произведения AA –1 :
|
Пример 6.
Найти
ранг матрицы
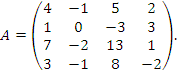
Решение. Непосредственным вычислением проверяется, что det A = 0. Следовательно, rank A < 4. Однако существует минор третьего порядка, отличный от нуля. Таким минором является, например, определитель, составленный из элементов первой, второй, третьей строк и второго, третьего, четвертого столбцов. Следовательно, rank A = 3.
Примеры 7-10.
|
1. Решить систему уравнений
методом Гаусса. Решение. Рассмотрим расширенную матрицу и приведем ее к треугольному виду, выполняя операции над строками:
Полученная матрица описывает систему уравнений
эквивалентную исходной системе. Решение находится элементарно:
Убедимся
в том, что полученный набор
|
***
|
2. Решить систему уравнений
методом Гаусса. Решение. Преобразуем расширенную матрицу, производя элементарные операции над строками:
Третья строка этой матрицы соответствует уравнению
не имеющему решений и, следовательно, система является несовместной. |
***
|
3. Решить систему уравнений
методом Гаусса. Решение. Производя элементарные преобразования над строками, приведем расширенную матрицу к ступенчатой форме:
Выпишем соответствующую систему уравнений:
Последнее
уравнение содержит две переменных,
одну из которых нужно рассматривать
в качестве свободного параметра.
Назначим этому параметру произвольное
значение
Таким образом, общее решение системы имеет вид
Если
подставить вместо c
произвольное число, например нуль, то
мы получим частное решение:
Подставляя
c
= 2, получаем другое частное решение:
Таким
образом, данная система имеет бесконечное
множество решений.
Проверка:
Подставим
Уравнения обратились в тождества. |
Решить методом Крамера систему линейных уравнений:

Решение. Вычислим определители, выполняя предварительно элементарные преобразования над их строками и затем разлагая полученные определители по элементам их первых столбцов.


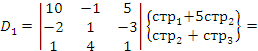
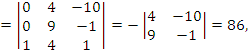


Пример
11.Найти
равнодействующую двух сил
![]() и
и![]() ,
модули которых равныF1
= 5, F2
= 7, угол между ними θ = 60°.
Определить также углы α и β, образуемые
равнодействующей с силами
,
модули которых равныF1
= 5, F2
= 7, угол между ними θ = 60°.
Определить также углы α и β, образуемые
равнодействующей с силами
![]() и
и![]() .
.
Решение.
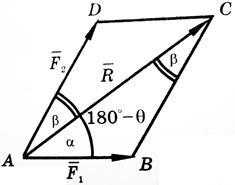
По формуле
![]()
![]()
находим
![]()
![]()
Пример 12.
При
каких значениях α
и β
вектор ![]() перпендикулярен
вектору
перпендикулярен
вектору ![]() ,
если
,
если ![]() ?
?
Решение.
Так
как
![]() ,
то
,
то![]() ;
откудаβ
= ±2. Векторы
;
откудаβ
= ±2. Векторы
![]() и
и![]() перпендикулярны,
тогда, когда
перпендикулярны,
тогда, когда![]() ,
т. е. 3·2 + (-1)·β
+ α·1
= 0; откуда α
= β
- 6.
,
т. е. 3·2 + (-1)·β
+ α·1
= 0; откуда α
= β
- 6.
При β = 2, имеем α = 2 - 6 = -4; при β = -2, имеем α = -2 - 6 = -8.
Пример 13.
Векторы
![]() лежат
в одной плоскости и образуют попарно
друг с другом углы 2π/3.
Разложить вектор
лежат
в одной плоскости и образуют попарно
друг с другом углы 2π/3.
Разложить вектор
![]() по
векторам
по
векторам![]() и
и![]() ,
если
,
если![]()
![]() .
.
Решение.
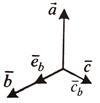
Найдем
единичные векторы, направленные, как и
векторы
![]() и
и![]() (см.
рисунок):
(см.
рисунок):![]()
![]() или
или![]()
![]() .
Тогда
.
Тогда![]() и
и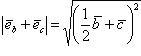

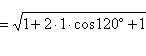
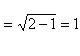 .
.
Следовательно,
вектор
![]() -
единичный.
-
единичный.
Так
как
![]() ,
то угол между векторами
,
то угол между векторами![]() и
и![]() равен
180°, т. е. эти векторы противоположно
направлены; поэтому
равен
180°, т. е. эти векторы противоположно
направлены; поэтому![]()
![]() .
.
Пример 14.
Определить
координаты точки C
- середины вектора
![]() по
известным радиусам-векторам его концовA
и B.
по
известным радиусам-векторам его концовA
и B.
Решение.
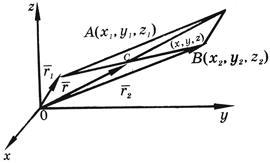
Пусть
радиусы-векторы точек A
и B
соответственно равны
![]() и
и![]() .
Середина отрезкаAB
будет находиться на пересечении
диагоналей параллелограмма, построенного
на векторах
.
Середина отрезкаAB
будет находиться на пересечении
диагоналей параллелограмма, построенного
на векторах
![]() и
и![]() ,
и тогда точкаC
определится радиусом-вектором
,
и тогда точкаC
определится радиусом-вектором
![]() ,
который равен полусумме векторов
,
который равен полусумме векторов![]() и
и![]() ,
т. е.
,
т. е.
![]()
![]() (1)
(1)
Координаты точки A обозначим через x1, y1 и z1, координаты точки B - через x2, y2 и z2, а координаты точки C - через x, y и z.
Спроектируем
векторное равенство (1) на оси координат
по формулам (9).
Так как векторы
![]() ,
,![]() и
и![]() являются
радиусами-векторами точекC,
A
и B,
то их проекции на координатные оси будут
равны
являются
радиусами-векторами точекC,
A
и B,
то их проекции на координатные оси будут
равны
rx = x; ry = y; rz = z; r1x = x1; r1y = y1; r1z = z1;
r2x = x2; r2y = y2; r2z = z2.
Тогда векторное равенство (1) заменится такими тремя скалярными равенствами, определяющими координаты середины отрезка по известным координатам его концов,
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Даны
два вектора:
![]()
![]() и
и![]()
![]() .
Найти проекции на координатные оси
суммы и разности этих векторов.
.
Найти проекции на координатные оси
суммы и разности этих векторов.
Решение.
Составим сумму и разность этих векторов:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример 15.
Дан
треугольник ABC.
Прямая l
пересекает прямые BC,
CA,
AB
в точках A1,
B1,
C1.
Доказать, что векторы
![]()
![]() коллинеарны.
коллинеарны.
Решение.

Обозначим
(см. рисунок)
![]()
![]() (1) или
(1) или![]()
![]()
![]() ,
откуда
,
откуда![]()
![]() (2).
(2).
Выразим
вектор
![]() через
векторы
через
векторы![]() и
и![]() .
Имеем
.
Имеем![]() .
Но из (2) следует, что
.
Но из (2) следует, что![]() ,
а из (1) - что
,
а из (1) - что![]()
![]() .
.
Следовательно,
![]()
![]() или
или![]()
![]() (3).
(3).
Таким образом,
![]()
![]()
![]()
![]() (4)
(4)
Аналогично, используя (1) - (3), находим
![]()
![]()
![]()
![]()
![]()
![]()
![]() (5)
(5)
Для доказательства
коллинеарности векторов
![]() и
и![]() ,
установим, что отношения коэффициентов
при
,
установим, что отношения коэффициентов
при![]() и
и![]() в
(4) и (5) равны. Для этого проведем прямую
в
(4) и (5) равны. Для этого проведем прямую![]() ,
которая пересечетC1B1
в точке D.
,
которая пересечетC1B1
в точке D.
Тогда ΔC1A1B ~ ΔA1CD1, а ΔAC1B1 ~ ΔCDB1, откуда
![]()
![]() (6)
(6)
и
![]()
![]() (7)
(7)
Так как из (1)
следует, что
![]()
![]() .
Далее находим
.
Далее находим![]()
![]()
(см.
(7)). Значит,mnp
= -1 (8).
Теперь найдем
отношения коэффициентов при
![]() и
и![]() в
(4) и (5):
в
(4) и (5):
![]()
![]() (9) и
(9) и ![]()
![]() (10).
(10).
Из (8) следует, что
![]() ;
подставляя это значение в (10), получим,
что указанное отношение равно
;
подставляя это значение в (10), получим,
что указанное отношение равно![]() ,
т. е. совпадает с (9).
,
т. е. совпадает с (9).
Таким образом
доказали, что
![]()
![]() .
Аналогично доказывается, что
.
Аналогично доказывается, что![]()
![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
Пример 16.
Дан
вектор
![]()
![]()
![]() .
Найти его проекциюaL
на ось L,
составляющую с координатными осями
равные острые углы.
.
Найти его проекциюaL
на ось L,
составляющую с координатными осями
равные острые углы.
Решение.
По условию направляющие косинусы оси проекций между собой равны:
![]()
![]()
![]()
Но сумма квадратов направляющих косинусов какого-либо направления равна 1, а потому
![]()
![]()
![]()
и так как в этой сумме все слагаемые между собой равны, то
![]()
![]()
![]()
![]()
тогда
![]()
![]()
![]()
(знак
плюс перед корнем взят потому, что по
условию углы
![]() ,
,![]() и
и![]() -
острые, а значит, косинусы их положительны).
Так как по условиюax
= 2; ay
= 5; az
= 1, то по формуле
-
острые, а значит, косинусы их положительны).
Так как по условиюax
= 2; ay
= 5; az
= 1, то по формуле
![]()
![]()
![]()
![]()
![]()
получаем
![]()
![]()
![]()
![]()
![]()
Пример 17.
Найти
углы, которые прямая
![]()
![]()
![]() составляет
с координатными осями.
составляет
с координатными осями.
Решение.
По формулам (2), полагая в них m = 2, n = 3, p = 6, будем иметь
![]()
![]()
![]() ,
или
,
или
![]() ;
;
![]()
![]()
![]()
Проверьте,
что
![]()
![]()
![]() .
.
Острые
углы, составляемые прямой с координатными
осями, равны:
![]()
![]()
![]() (эти
значения определены по таблицам
тригонометрических функций).
(эти
значения определены по таблицам
тригонометрических функций).
Пример 18.
Общие
уравнения
прямой
![]()
![]()
![]() (*)
преобразовать
к каноническому виду(1).
(*)
преобразовать
к каноническому виду(1).
Решение.
Из системы (*) исключим сначала y и выразим z через x, потом исключим x и выразим z уже через y.
1) Для того, чтобы из системы (*) исключить y, умножим второе из уравнений системы (*) на 3 и сложим его почленно с первым. Получим, что 7x - z - 7 = 0, откуда z = 7x - 7,
![]()
![]()
2) Умножая первое уравнение из (*) на -2 и складывая почленно со вторым, получим, исключая x из системы (*),
-7y + 9z - 14 = 0,
откуда
9z = 7y + 14;
![]()
![]()
или
![]()
![]()
Сравнивая найденные значения z, получаем уравнения прямой в каноническом виде

![]() ,
или
,
или
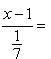
![]()
![]() .
.
Умножая теперь все знаменатели на 7, окончательно получим
![]()
![]()
![]()
Приведем второй способ решения.
Если общие уравнения прямой записываются в виде

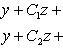
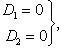 (A)
(A)
то уравнения прямой с направляющими коэффициентами имеют вид


 (B)
(B)
где x0, y0 и z0 - координаты одной из точек, через которую проходит прямая (А).
Из уравнений (B) усматриваем, что направляющие коэффициенты прямой m, n и p определяются по формулам



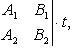 (C)
(C)
в которых можно положить t = 1.
Решим нашу задачу по этому способу. Определим одну из точек, через которую проходит данная прямая (*). Дадим координате z значение нуль (z = 0). Для определения абсциссы x и ординаты y этой точки получим систему уравнений
![]()
![]()
![]()
или
![]()
![]()
из которой x = 1; y = -2. Итак, одна из точек, через которую проходит прямая, известна. Ее координаты (1, -2, 0). Чтобы определить направляющие коэффициенты прямой по формулам (С), в которых взято t = 1, составляем матрицу из коэффициентов уравнений системы (*):
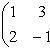
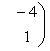
и получаем
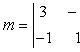
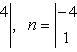


m = -1; n = -9; p = -7.
Уравнения прямой (*) в каноническом виде с учетом того, что прямая проходит через точку (1, -2, 0), примут вид
![]()
![]()
![]()
Умножая все знаменатели на -1, получим окончательно
![]()
![]()
![]()
Пример 19.
Уравнения
прямой
![]()
![]()
![]() преобразовать
к каноническому виду и определить углы,
образуемые этой прямой с координатными
осями.
преобразовать
к каноническому виду и определить углы,
образуемые этой прямой с координатными
осями.
Решение.
Определим одну из точек, принадлежащую данной прямой. Положим z = 0 и определим координаты x и y, получим систему уравнений
![]()
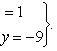
Отсюда находим x = -3; y = -1.
Итак, определена точка (-3, -1, 0), через которую проходит прямая.
Воспользовавшись для определения m, n и p формулами



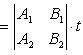
при t = 1, получим
m = -19; n = 9; p = 11.
Искомое уравнение в виде (1) запишется так:
![]()
![]()
![]() (A)
(A)
Углы, образованные этой прямой с координатными осями, определяем по формулам (2), в которых m, n и p имеют только что найденные значения:
![]()
![]()
![]()
![]()
![]()
![]()
Контроль.
![]()
![]()
![]() .
По известным косинусам углов находим
углы
.
По известным косинусам углов находим
углы![]()
![]()
![]()
![]() (при
определении углов из двух возможных
знаков у косинусов выбран верхний знак).
(при
определении углов из двух возможных
знаков у косинусов выбран верхний знак).
Уравнения прямой получились бы в другом виде, если бы вместо точки (-3, -1, 0) на прямой взяли бы какую-либо другую точку. Числители дробей в (А) изменились бы, но знаменатели остались теми же. Если же решать эту задачу по первому способу задачи, то в знаменателях могли бы получиться числа, пропорциональные тем, которые стоят в знаменателях дробей (А).
Пример 20.
Найти
уравнения плоскостей, проектирующих
прямую
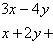
![]()
![]() (1)
на
координатные плоскости.
(1)
на
координатные плоскости.
Решение.
Чтобы найти уравнение плоскости, проектирующей прямую (1) на плоскость xOy, надо из системы (1) исключить координату z. Умножая первое уравнение этой системы на -3, а второе на 5 и складывая полученные уравнения, будем иметь -4x + 22y + 34 = 0, а сокращая на -2, получим искомое уравнение в виде 2x - 11y - 17 = 0.
Уравнение плоскости, проектирующей прямую (1) на плоскость xOz, получим, исключая из системы (1) координату y. Умножая второе уравнение в системе (1) на 2 и складывая с первым, получим искомое уравнение в виде
5x + 11z + 29 = 0.
Уравнение плоскости, проектирующей прямую (1) на плоскость yOz, получим, исключая из системы (1) координату x. Умножая второе уравнение в системе (1) на -3 и складывая с первым, получим искомое уравнение в виде
5y + 2z + 13 = 0.
Пример 21.
Написать уравнение окружности с центром в точке C(2, -3) и радиусом, равным 6.
Решение.
По уравнению
(x - a)2 + (y - b)2 = r2,
полагая в нем a = 2, b = -3, r = 6, сразу имеем (x - 2)2 + (y + 3)2 = 36, или x2 + y2 - 4x + 6y - 23 = 0.
Пример 22.
Показать, что x2 + y2 + 4x - 6y - 3 = 0 есть уравнение окружности. Найти ее центр и радиус.
Решение.
Заданное уравнение преобразуем к виду
(x - a)2 + (y - b)2 = r2. (1)
Выпишем члены, содержащие только x, и члены, содержащие только y. Легко проверить, что
x2 + 4x = (x + 2)2 - 4,
y2 - 6y = (y - 3)2 - 9.
Левая часть уравнения запишется теперь так:
![]()
![]()
![]()
или отсюда
(x + 2)2 + (y - 3)2 = 16. (2)
Сравнивая уравнение (2) с (1), заключаем, что уравнение определяет окружность, центр которой имеет координаты C(-2, 3), r2 = 16, а r = 4.
Пример 23.
Составить
простейшее уравнение эллипса, зная,
что:
а) его полуоси a
= 6, b
= 4;
б) расстояние между фокусами 2c
= 10, а большая полуось 2a
= 16;
в) большая полуось a
= 12, а эксцентриситет e
= 0,5;
г) малая полуось b
= 8, а эксцентриситет e
= 0,6;
д) сумма полуосей a
+ b
= 12, а расстояние между фокусами
![]() .
.
Решение.
а)
Простейшее уравнение эллипса имеет вид
![]()
![]() .
Подставляя сюдаa
= 6, b
= 4, получим
.
Подставляя сюдаa
= 6, b
= 4, получим
![]()
![]()
б) Имеем 2c = 10; c = 5; 2a = 16; a = 8.
Чтобы написать уравнение эллипса, следует найти малую полуось b. Между величинами a, b и c у эллипса существует зависимость a2 - b2 = c2, или b2 = a2 - c2. В нашем случае b2 = 64 - 25 = 39, и уравнение эллипса будет иметь вид
![]()
![]()
в)
a
= 12; e
= 0,5; известно, что
![]() ;
в этой формуле неизвестноc.
Для его определения получаем уравнение
;
в этой формуле неизвестноc.
Для его определения получаем уравнение
![]()
![]()
отсюда c = 6.
Теперь, зная, что a = 12, c = 6, пользуясь отношением a2 - c2 = b2, найдем, что b2 = 144 - 36 = 108; a2 = 144.
Уравнение
будет
![]()
![]() .
.
г) b
= 8; e
= 0,6;
![]() ,
отсюда
,
отсюда![]()
![]() .
Напишем соотношениеa2
- c2
= b2
и подставим в него c
= 0,6a;
b
= 8. Получим a2
= 0,36a2
= 64; 0,64a2
= 64; a2
= 100.
.
Напишем соотношениеa2
- c2
= b2
и подставим в него c
= 0,6a;
b
= 8. Получим a2
= 0,36a2
= 64; 0,64a2
= 64; a2
= 100.
Уравнение эллипса будет иметь вид
![]()
![]()
д) a
+ b
= 12,
![]() .
.
Для определения
уравнения эллипса надо знать a
и b.
Нам известно, что
![]() ;c2
= 18; a2
- b2
= c2.
;c2
= 18; a2
- b2
= c2.
Поэтому (a + b)(a - b) = 18. Подставляя сюда a + b = 12, найдем, что a - b = 1,5.
Решая систему уравнений
![]()
![]()
получим, что a = 6,75, b = 5,25. Уравнение эллипса запишется в виде
![]()
![]()
![]()
Пример 24.
Найти точки пересечения окружности (x - 1)2 + (y - 2)2 = 4 и прямой y = 2x.
Решение.
Координаты точек пересечения должны удовлетворять обоим указанным уравнениям, так как эти точки находятся как на одной, так и на другой линии. Решим систему уравнений
![]()
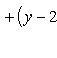

Подставляя в первое уравнение 2x вместо y и раскрывая скобки, получим
x2 - 2x + 1 + 4x2 - 8x + 4 = 4,
или
5x2 - 10x + 1 = 0,
а отсюда
![]()
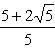
![]()

Подставляя эти значения во второе уравнение y = 2x, получим
![]()

![]()
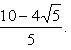
Искомыми точками пересечения будут A(x1, y1), B(x2, y2):

 и
и
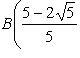
 .
.
Номер варианта определяется последней цифрой порядкового номера (а не чисел, обозначающих факультет, специальность или длительность обучения) зачетки (студенческого билета). Если последняя цифра 0, то вариант 10.
Вариант № 1
1.Найти косинус угла между векторами AB и АС
А(2, –2, 3), В(1, – 1, 2), С(4, –4, 5)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей

3.Решить систему уравнений по правилу Крамера
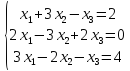
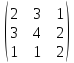
4.Найти
матрицу С–1
, обратную матрице С=
5.Написать
разложение вектора
 по векторам
по векторам ,
, ,
,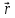
 ={-2,
0, 9}
={-2,
0, 9}
 ={0,-1,2}
={0,-1,2}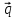 ={1,
0, -1}
={1,
0, -1} ={-1,
2, 4}
={-1,
2, 4}
6. Написать уравнение окружности с центром в точке C(3, -5) и радиусом, равным 6.
Вариант № 2
1.Найти косинус угла между векторами AB и АС
А(0, –2, 6), В(–12, – 2, –3), С(–9, –2, –6)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей

3.Решить систему уравнений по правилу Крамера
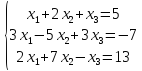
4.Найти
матрицу С–1
, обратную матрице С=

5.Написать
разложение вектора
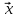 по векторам
по векторам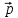 ,
,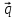 ,
,
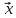 ={5,
-12, -1}
={5,
-12, -1}
 ={1,-3,0}
={1,-3,0}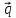 ={1,
-1, 1}
={1,
-1, 1}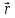 ={0,
-1, 2}
={0,
-1, 2}
6. Показать, что x2 + y2 + 2x - 6y - 3 = 0 есть уравнение окружности. Найти ее центр и радиус.
Вариант № 3
1.Найти косинус угла между векторами AB и АС
А(2, 3, –1), В(4, 5, –2), С(3, 1, 1)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей
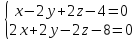
3.Решить систему уравнений по правилу Крамера
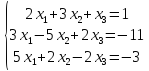
4.Найти
матрицу С–1
, обратную матрице С=
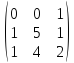
5.Написать
разложение вектора
 по векторам
по векторам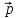 ,
,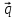 ,
,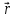
 ={0,
2, 4}
={0,
2, 4}
 ={3,
1, -1}
={3,
1, -1}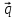 ={0,
-3, 1}
={0,
-3, 1}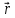 ={1,
1, 1}
={1,
1, 1}
6. Найти координаты центра и радиус окружности x2 + y2 - x + 4y - 1 = 0.
Вариант № 4
1.Найти косинус угла между векторами AB и АС
А(1, 2, –2), В(3, 4, –5), С(1, 1, 0)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей
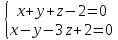
3.Решить систему уравнений по правилу Крамера

4.Найти
матрицу С–1
, обратную матрице С=
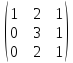
5.Написать
разложение вектора
 по векторам
по векторам ,
,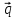 ,
,
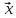 ={–1,
5, 5}
={–1,
5, 5}
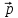 ={2,
1, 1}
={2,
1, 1} ={–2,
0, –3}
={–2,
0, –3} ={–1,
2, 1}
={–1,
2, 1}
6. Дана окружность x2 + y2 = 9. Составить уравнение прямой l, параллельной оси абсцисс и пересекающей окружность в таких точках M и N, что MN = 1.
Вариант № 5
1.Найти косинус угла между векторами AB и АС
А(–2, –2, 0), В(1, – 2, 4), С(5, –2, 1)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей
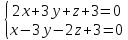
3.Решить систему уравнений по правилу Крамера

4.Найти
матрицу С–1
, обратную матрице С=

5.Написать
разложение вектора
 по векторам
по векторам ,
,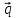 ,
,
 ={–1,
–2, 3}
={–1,
–2, 3}
 ={2,
0, 1}
={2,
0, 1} ={
1, 2, –1}
={
1, 2, –1}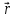 ={0,
4 –1}
={0,
4 –1}
6. Найти точки пересечения окружности (x -2)2 + (y - 4)2 =16 и прямой y = 2x.
Вариант № 6
1.Найти косинус угла между векторами AB и АС
А(3, 3, –1), В(3, 2, 0), С(4, 4, –1)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей
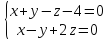
3.Решить систему уравнений по правилу Крамера

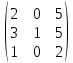
4.Найти
матрицу С–1
, обратную матрице С=
5.Написать
разложение вектора
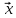 по векторам
по векторам ,
, ,
,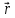
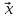 ={–5,
2, –1}
={–5,
2, –1}
 ={–1,
1, 0}
={–1,
1, 0}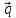 ={
2, –1, 3}
={
2, –1, 3} ={
1, 0, 1}
={
1, 0, 1}
6. Составить простейшее уравнение эллипса, зная, что: а) его полуоси a = 6, b = 2; б) расстояние между фокусами 2c = 10, а большая полуось 2a = 18; в) большая полуось a = 10, а эксцентриситет e = 0,5.
Вариант № 7
1.Найти косинус угла между векторами AB и АС
А(–1, –7, –4), В(2, – 1, –1), С(4,3, 1)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей
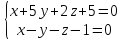
3.Решить систему уравнений по правилу Крамера

4.Найти
матрицу С–1
, обратную матрице С=
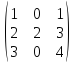
5.Написать
разложение вектора
 по векторам
по векторам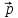 ,
, ,
,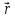
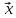 ={
1, –5, 7}
={
1, –5, 7}
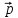 ={
0, –1, 1}
={
0, –1, 1}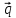 ={
2, 0, 1}
={
2, 0, 1}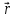 ={
3, –1, 0}
={
3, –1, 0}
6. Найти длины осей, координаты фокусов и эксцентриситет эллипса 2x2 + 9y2 = 144.
Вариант № 8
1.Найти косинус угла между векторами AB и АС
А(2, –2, 6), В(0, 0, 4), С(6, –6, 10)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей

3.Решить систему уравнений по правилу Крамера

4.Найти
матрицу С–1
, обратную матрице С=

5.Написать
разложение вектора
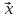 по векторам
по векторам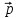 ,
, ,
,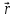
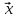 ={
5, 1, 4}
={
5, 1, 4}
 ={
2, 0, 2}
={
2, 0, 2} ={
0, –1, 1}
={
0, –1, 1}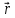 ={
3, –1, 4}
={
3, –1, 4}
6. Составить простейшее уравнение эллипса, зная, что: а) его полуоси a = 6, b = 4; б) расстояние между фокусами 2c = 10, а большая полуось 2a = 16; в) сумма полуосей a + b = 12, а расстояние между фокусами 2c=6*21/2.
Вариант № 9
1.Найти косинус угла между векторами AB и АС
А(0, 1, 0), В( 3, 1, 4), С(4, 1, 3)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей
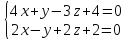
3.Решить систему уравнений по правилу Крамера
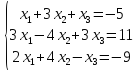
4.Найти
матрицу С–1
, обратную матрице С=

5.Написать
разложение вектора
 по векторам
по векторам ,
, ,
,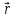
 ={
1, 1, –1}
={
1, 1, –1}
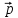 ={
1, 1, 0}
={
1, 1, 0} ={
–1, 0, 1}
={
–1, 0, 1} ={
–1, 0, 2}
={
–1, 0, 2}
6. Составить уравнение окружности, проходящей через точку A (4; 1) и касающейся осей координат.
Вариант № 10
1.Найти косинус угла между векторами AB и АС
А( 3, 2, 0), В(1, 4, – 1), С(4, 0, 2)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей

3.Решить систему уравнений по правилу Крамера
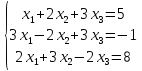
4.Найти
матрицу С–1
, обратную матрице С=

5.Написать
разложение вектора
 по векторам
по векторам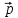 ,
, ,
,
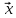 ={
–3, 7, 4}
={
–3, 7, 4}
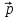 ={
–2, 2, 1}
={
–2, 2, 1} ={
2, 0, 1}
={
2, 0, 1}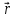 ={
1, 1, 1}
={
1, 1, 1}
6. Найти точки пересечения окружности (x - 1)2 + (y - 2)2 = 4 и прямой y = 2x.
II.Элементы функционального и комплексного анализа.
Понятие множества.
В группе из 100 туристов 70 человек знают английский язык, 45 знают французский язык и 23 человека знают оба языка. Сколько туристов в группе не знают ни английского, ни французского языка?
Решение задачи:
Обозначим: U – универсальное множество, т.е. множество всех туристов,
А – множество туристов, знающих английский язык,
B – множество туристов, знающих французский язык.
Проиллюстрируем:
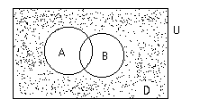
Необходимо найти количество туристов, не знающих ни одного языка, т.е. количество элементов множества D = U \ (AB)(на рисунке заштриховано).
Дано(по условию):m(U) = 100 (чел.)
m(A) = 70 (чел.)
m(B) = 45 (чел.)
m(AB) = 23 (чел.)
Найти: ` m(D) = m(U) – m(AB) - ?
Решение: Используя формулу, находим количество туристов, знающих хотя бы один язык:
m(AB) = m(A) + m(B) – m(AB) = 70 + 45 - 23 = 92,
количество туристов, не знающих ни одного языка:
m(D) = m(U) - m(AB) = 100 – 92 = 8 (чел.)
Ответ: 8 чел.
Аналогично решить задачи № 2, 3, 4.
Из 40 предложений 30 содержат предлог «в», 27 предлог «на», в пяти предложениях нет ни того, ни другого. Сколько предложений содержат оба предлога?
20 мальчиков поехали на пикник. При этом 5 из них обгорели, 8 были сильно покусаны комарами, а 10 остались всем довольны. Сколько обгоревших мальчиков не было покусано комарами? Сколько покусанных комарами мальчиков также и обгорели? (Сформулируйте эту задачу как: 1) лингвистическую, например: анализ наличия 2 морфем в словах; 2) в общем виде, используя понятия: множество, подмножества и их элементы).
В штучном отделе магазина посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет, В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?
В олимпиаде по иностранному языку принимало участие 40 студентов, им было предложено ответить на один вопрос по лексикологии, один по страноведению и один по стилистике. Результаты проверки ответов представлены в таблице:
|
Получены правильные ответы на вопросы |
Колич-во ответивших |
|
по лексикологии |
20 |
|
по страноведению |
18 |
|
по стилистике |
18 |
|
по лексикологии и страноведению |
7 |
|
по лексикологии и стилистике |
8 |
|
по страноведению и стилистике |
9 |
Известно также, что трое не дали правильных ответов ни на один вопрос. Сколько студентов правильно ответили на все три вопроса? Сколько студентов правильно ответили ровно на два вопроса?
Решение задачи:
Обозначим:
U – универсальное множество, т.е. множество всех студентов,
A – множество студентов, правильно ответивших на вопросы по лексикологии,
B – множество студентов, правильно ответивших на вопросы по страноведению,
С – множество студентов, правильно ответивших на вопросы по стилистике,
D - множество студентов, не давших ни одного правильного ответа.
Проиллюстрируем:

Дано (по условию): m(U) = 40 (чел.) m(D) = 3 (чел.)
m(A) = 20 (чел.) m(AB) = 7 (чел.)
m(B) = 18 (чел.) m(AC) = 8 (чел.)
m(C) = 18 (чел.) m(BC) = 9 (чел.)
Найти: 1) m(ABC) - ? 2) сколько студентов ответили ровно на 2 вопроса?
Решение:
1) Пересечение трех множеств разбивает универсальное множество на классы, т.е. на попарно непересекающиеся непустые подмножества. Обозначим число элементов в каждом классе маленькими латинскими буквами (см. рисунок). Можно проверить (и доказать!), что
m(ABC) = m(A) + m(B) + m(C) – m(AB) – m(AC) – m(BC) + m(ABC)
Очевидно, что m(ABC) = m(U) – m(D) = 40 – 3 = 37
Подставив в формулу известные данные, получим:
37 = 20 + 18 + 18 – 7 – 8 – 9 + m(ABC) m(ABC) = 5
Итак, на три вопроса ответили 5 студентов
2) Чтобы найти количество студентов, правильно ответивших ровно на два вопроса, необходимо найти и сложить d, e, f:
d + e + f = (8 – m(ABC)) + (7 – m(ABC)) + (9 – m(ABC)) = 3 + 2 + 4 = 9
Ответ: 1) 5; 2) 9
Теорема о количестве подмножеств конечного множества.
Рассмотрим множество А = {1, 2, 3 }, где |A| = 3, и множество В = {5, 6, 7, 8}, где |B| = 4.
Составим всевозможные подмножества множества А:
А, , {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}.
Всего получили 8 подмножеств.
Составим всевозможные подмножества множества В:
В, , {5}, {6}, {7}, {8}, {5,6}, {5,7}, {5,8}, {6,7}, {6,8}, {7,8}, {5,6,7}, {5,7,8}, {6,7,8}, {5,6,8}.
Получили 16 подмножеств.
Используя результаты рассмотренных примеров, можно предположить справедливость следующего равенства: n = 2m, где n – количество подмножеств данного конечного множества, m – мощность множества.
Справедливость предположения подтверждает теорема, которую мы примем без доказательства.
Теорема: Если для конечного множества А его мощность равна т, то количество всех подмножеств данного множества, обозначаемое Р(А), равно 2т.
Пример: Вычислить количество подмножеств множества М – делителей числа 20.
Составим множество М и найдем его мощность :
М = {1,2,4,5,10,20}. Мощность |M| = 6, тогда количество подмножеств равно Р(М) = 26 = 64.

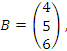 .
Тогда
.
Тогда




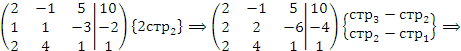

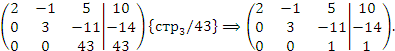

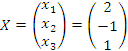 обращает
каждое уравнение данной системы в
тождество:
обращает
каждое уравнение данной системы в
тождество:

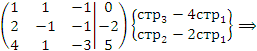

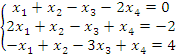
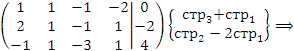
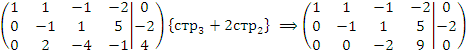
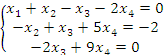
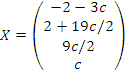
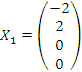 .
.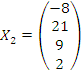 .
.