Papka_Vz_dlya_bakalavrov_2014g / Папка Вз. Лекции / лкция№14 .Решение обратных задач Р. Ц

Лекция №14

РЕШЕНИЕ ОБРАТНЫХ ЗАДАЧ РАСЧЁТОВ Р.Ц.

1 Строится и анализируется расчётная размерная цепь (рисунок 3.8).

Приведенная на рисунке 3.8 схема размерной цепи условная, конкретный пример решения задач размерных цепей – ниже.

Рисунок 3.8 – Размерная цепь «А»

В данной размерной цепи звено А_∆ - замыкающее; звенья ; ; ; – составляющие, уменьшающие; звено – составляющее, увеличивающее.

Как отмечено выше, при решении обратной задачи известны номинальные размеры всех звеньев, и допуски (предельные отклонения) составляющих звеньев.

Требуется определить допуск (предельные отклонения замыкающего звена А_∆).

2 Проверка правильности построения схемы размерной цепи «A»

2.1 Номинальный размер замыкающего звена

А_∆ = - - - - (3.1)

У правильно построенной цепи размер, полученный решением (3.1), должны соответствовать этому размеру по чертежу. И обязательно цепь размеров должна быть замкнутой.

В общем случае

А_∆ = (3.2)

где - увеличивающие составляющие звенья;

- уменьшающие составляющие звенья;

n - число увеличивающих составляющих звеньев;

m - число всех звеньев размерной цепи (составляющие плюс замыкающие);

i - номера звеньев размерной цепи;

Рисунок 3.9 – Графическое изображение ряда номеров звеньев размерной цепи i

2.2 Допуск замыкающего звена А_∆ определяется разностью его предельных размеров

Предельные размеры замыкающего звена определяются по формулам:

(3.3)

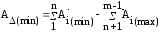(3.4)

Вычитая из 3.3 3.4, и учитывая, что

– сумма допусков увеличивающих звеньев,

– сумма допусков уменьшающих звеньев,

определяется допуск замыкающего звена, как сумма допусков всех составляющих звеньев размерной цепи

(3.5)

2.3 Предельные отклонения замыкающего звена

Предельные отклонения замыкающего звена определяется разностью предельных его размеров и номинального размера.

Верхнее отклонение: ES A_∆= A_∆(max) - A_∆, (3.6)

Нижнее отклонение: ES A_∆= A_∆(min) - A_∆. (3.7)

Решая совместно 3.6,3.7 и 3.2,3.3,3.4, предельные отклонения замыкающего звена можно определить через соответствующие разности предельных отклонений увеличивающих и уменьшающих составляющих звеньев размерной цепи.

(3.8)

(3.9)

4