Metod_FMYa

Данная формула записана для системы координат, в которой ось Z совпадает с вектором намагниченности M0. Размагничивающие факторы вдоль направлений 1, 2 и 3 (рис. 6.4.) равны соответственно:

Таким образом, измерив резонансные поля вдоль легкого и трудного направлений в плоскости пленки, а также вдоль нормали к плоскости, можно с помощью уравнений (6.13 – 6.15) определить гиромагнитное отношение и

эффективные поля одноосной и ромбической компонент анизотропии. По полученным данным при известном значении намагниченности рассчитываются константы анизотропии Kuи Kr .

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Регистрация линий поглощения и измерения резонансных полей в настоящей работе производится на радиоспектрометре РЭ-1301, принцип действия которого и его блок-схема описаны в работе № 3.

ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА

1. Ознакомиться с устройством радиоспектрометра РЭ-1301.

41

2. Включить радиоспектрометр, измеритель магнитной индукции (ЯМР – магнитометр) Ш1-1 и частотомер. Выдержать приборы включенными в течение

5 – 10 минут и произвести настройку.

3. Закрепить пленку феррита-граната в держатель и поместить в резона-

тор радиоспектрометра.

4. Снять угловую зависимость резонансного поля в плоскости пленки,

изменяя азимутальный угол с шагом 100 от 0 до 1800.

5. Записать линию поглощения ФMP при перпендикулярной ориентации постоянного магнитного поля относительно плоскости пленки и измерить резо-

нансное поле H3.

мальным точкам производной линии поглощения – точкам перегиба первооб-

разной.

2. Вычислить резонансное значение постоянного магнитного поля H3

при перпендикулярной ориентации относительно пленки:

4. Построить зависимость Hp . По полученной зависимости опреде-

лить минимальное H1 и максимальное H2 резонансные поля.

5. С помощью формул (6.13 – 6.15) вычислить эффективные поля одноос-

ной Huэф и ромбической Hrэф компонент анизотропии, а также гиромагнитное отношение и g-фактор. По заданным значениям намагниченности рассчитать константы одноосной и ромбической анизотропии. Вычислить среднеквадра-

тичные погрешности этих величин.

42

6. По найденным значениям g-фактора определить природу магнитного

момента в исследованных пленках.

7. ИССЛЕДОВАНИЕ СПИНОВЫХ ВОЛН И ОПРЕДЕЛЕНИЕ

КОНСТАНТЫ ОБМЕННОГО ВЗАИМОДЕЙСТВИЯ

ПО СПЕКТРУ СПИН-ВОЛНОВОГО РЕЗОНАНСА

Цель работы: изучение природы и основных характеристик спиновых волн, определение константы обменного взаимодействия в феррите-гранате.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Наличие сильной корреляции между магнитными моментами атомов магнитоупорядоченных веществ обусловливает возможность существования в таких системах, кроме однородной прецессии, неоднородных магнитных коле-

баний – обменных спиновых волн (рис.7.1). Существование таких волн связано

Рис. 7.1. а – однородный резонанс, б – бегущая спиновая волна, в – стоячая спиновая волна

с возрастанием энергии обменного взаимодействия вследствие непараллельно-

сти соседних элементарных магнитных моментов.

43

Микроскопическая модель. Рассмотрим цепочку из N спинов S и

предположим, что соседние спины связаны обменным взаимодействием типа

p 1

где J – обменный интеграл, а Sp – значение спина в узле кристаллической ре-

системы. Предположим, что в исследуемой системе спинов имеется один пере-

вернутый спин. Из формулы (7.1) следует, что такое изменение состояния при-

ведет к возрастанию энергии на величину 8JS2 и ее значение в этом случае за-

пишется: U1 U0 8JS2 . Возбуждения меньшей энергии можно представить,

если допустить, что спин повернут лишь частично. Элементарные возбуждения спиновой системы, обусловленные обменными силами, имеют волновой харак-

тер. Их называют спиновыми волнами, а когда они проквантованы – квазича-

стицами, магнонами с энергиями k k и квазиимпульсами pk k . Магно-

ны сходны с колебаниями кристаллической решетки, или фононами. Спиновые волны представляют собой распространение колебаний относительной ориен-

тации спинов в кристаллической решетке, аналогично упругим волнам в кри-

сталле, обусловленным колебаниями атомов относительно равновесных поло-

жений – узлов кристаллической решетки.

Дисперсионный закон для магнонов (спиновых волн) может быть выве-

ден следующим образом. Запишем отдельно слагаемые в сумме (7.1), которые

Данное выражение будет представлять собой не что иное, как обменную энер-

гию спина p. Магнитный момент этого спина ( p ) равен:

Это выражение имеет форму энергии магнитного момента p в магнитном по-

ле. Отсюда следует, что {[2J /(g B)](Sp 1 Sp 1)} Hp – эффективное маг-

нитное или обменное поле, которое действует на спин с номером p. Данный вывод позволяет записать уравнение движения, необходимое для последующе-

го анализа. В соответствии с уравнением вращательного движения, производ-

ная по времени от момента импульса Sp должна быть равна вращающему мо-

менту p Hp , действующему на спин p:

Если записать данное уравнение в проекциях на оси декартовой системы координат и решить полученную систему (решения будут иметь вид суперпо-

зиции гармоник), получим закон дисперсии для спиновых волн, или зависи-

мость частоты спиновой волны от волнового числа:

где a – расстояние между спинами. Соотношение (7.7) показывает, что в отли-

чие от колебаний решетки и электромагнитных волн, для которых частота пропорциональна k , для спиновых волн ~ k2.

Континуальный подход. Наличие обменного взаимодействия, сильно связывающего между собой элементарные магнитные моменты в магнитоупо-

рядоченных веществах, приводит к тому, что для описания процессов в этих веществах с успехом используется континуальный (или макроскопический, или квазиклассический) подход. При таком подходе мы отвлекаемся от микроско-

пического строения магнитоупорядоченного кристалла. Величиной, полностью характеризующей магнитное состояние ферромагнетика, является в этом случае макроскопическая намагниченность M . В соответствии с таким подходом об-

менная энергия, источником которой является электростатическое по своей

где U – однородная, а Uq – неоднородная ее части. Далее нас будет интересо-

вать неоднородная часть обменной энергии, возрастающая при быстром изме-

нении M в пространстве (непараллельности соседних магнитных моментов).

Для изотропной среды

где q = 2AM2 , A – константа неоднородного обменного взаимодействия,

равная 2JS2a. Вклад в эффективное поле Hэф, обусловленный Uq , или обмен-

ное поле hq будет определяться следующим выражением:

Задача заключается в определении закона дисперсии спиновых волн, т.е. зави-

симости от k . Пусть в намагниченном до насыщения ферромагнетике мо-

дуль и направление M0 не изменяется быстро в пространстве (кроме границ

Таким образом, когда имеет место пространственное изменение вектора намагниченности M , выражение для эффективного магнитного поля будет со-

держать дополнительный член (2AM2) 2m. Уравнение движения магнитно-

го момента M в эффективном поле Hэф имеет вид

46

систему уравнений, получим выражение для ВЧ-восприимчивости , которая связывает переменное магнитное поле h и переменную намагниченность:

Соотношение, определяющее резонансные поля спиновых волн в изо-

тропной пленке при перпендикулярной и параллельной ориентациях постоян-

ного поля H относительно ее плоскости, будет иметь следующий вид

Таким образом, из выражений (7.16) следует, что частота спиновых

волн ~ k2 .

В ферромагнетиках, кроме бегущих (рис. 7.1, а), возможно существова-

ние стоячих спиновых волн (рис. 7.1, б), для которых пространственная фаза колебаний остается постоянной. Возможность возбуждения стоячих спиновых волн однородным переменным магнитным полем впервые предсказал Киттель.

Это явление получило название спин-волнового резонанса (СВР). Исследова-

ния спин-волнового резонанса дают возможность получить богатую информа-

цию о фундаментальных величинах ферромагнитных веществ. В частности, для тонких пленок по наблюдаемым спектрам поглощения можно определить кон-

станту обменного взаимодействия А, время релаксации, гиромагнитное отно-

шение. Для возбуждения стоячих спиновых волн однородным переменным магнитным полем, т. е. наблюдения спин-волнового резонанса, необходимо обеспечить определенные граничные условия, приводящие к закреплению ("за-

мораживанию") спинов на одной или обеих поверхностях пленки. Один из та-

ких механизмов связан с поверхностной анизотропией, т.е. наличием очень тонкого приповерхностного слоя, в котором значение эффективного поля ани-

зотропии сильно отличается от значения поля анизотропии в основном объеме

47

пленки. Динамический механизм закрепления спинов возникает в многослой-

ных пленках с различающимися значениями поля однородного резонанса в слоях. Характерной особенностью такого механизма является резкая зависи-

мость спектра спин-волнового резонанса от направления постоянного магнит-

ного поля относительно пленки. Недавно был установлен новый, диссипатив-

ный механизм закрепления спинов, который возникает в многослойных плен-

ках с сильно различающимися значениями параметра затухания в слоях. Нали-

чие обменной связи между слоями, а также то обстоятельство, что даже в усло-

виях однородного резонанса угол прецессии вектора намагниченности M в

слое с большим параметром затухания 2 в 2 1 раз меньше, чем в слое с малым параметром затухания 1, приводит при возбуждении переменной на-

магниченности к возникновению узла стоячей спиновой волны на границе раз-

дела слоев или вблизи нее. Одно из качественных отличий диссипативного ме-

ханизма закрепления спинов заключается в независимости его действия от ори-

ентации внешнего магнитного поля H относительно пленки. В результате спектр СВР является практически изотропным. Это иллюстрирует рис.7.2, где приведены спектры СВР, записанные при различных углах H между посто-

янным магнитным полем и нормалью к плоскости пленки.

Рис.7.2

48

В данной работе для наблюдения СВР и определения константы обмен-

ного взаимодействия A используются дву- и трехслойные пленки с сильно раз-

личающимися значениями параметра затухания в слоях, в которых домини-

рующим является диссипативный механизм закрепления спинов. На границе раздела слоев должны выполняться так называемые обменные граничные усло-

вия, которые являются следствием непрерывности угла отклонения вектора M ,

а также непрерывности вращающего момента сил обменного поля:

На свободной поверхности, где имеет место свободная прецессия намаг-

ниченности, (dmdz) 0. Решение уравнения движения намагниченности с уче-

том граничных условий позволяет определить разрешенные значения волновых чисел k спиновых волн, которые могут возбуждаться однородным СВЧ-полем.

Когда магнитный момент полностью закреплен на обеих поверхностях слоя возбуждения, значения волновых чисел определяются выражением

где h – толщина пленки. В случае, когда магнитные моменты закреплены толь-

ко на одной стороне, а на другой имеет место свободная прецессия,

Таким образом, зная волновые числа возбуждаемых мод СВР и резонанс-

ные поля соответствующих пиков спектра СВР, можно, пользуясь резонансны-

ми соотношениями (7.16), определить значение константы обменного взаимо-

действия A. Процедура определения состоит в построении зависимости разно-

сти резонансных полей пиков нулевой и n-й мод спин-волнового резонанса как функции n 12 2 для двухслойной пленки и 2n 1 2 – для трехслойной. При полном закреплении спинов эта зависимость является линейной. Ее угловой ко-

эффициент равен 2A 2 .

Mh2

49

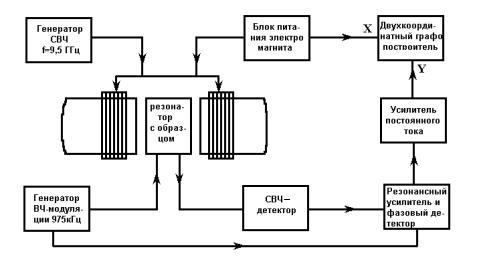
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Для исследования спин-волнового резонанса в данной работе используют установку, блок-схема которой показана на рис.7.3. Постоянное магнитное поле создается электромагнитом ФЛ-1, который питается от стабилизированного блока питания, позволяющего производить развертку поля с необходимой ско-

ростью в автоматическом и ручном режимах. В качестве источника сверхвысо-

кочастотного (СВЧ) электромагнитного поля используется клистронный гене-

ратор со встроенным аттенюатором. СВЧ-колебания от генератора через фер-

ритовый вентиль и согласователь по волноводу подаются в прямоугольный ре-

зонатор с модой колебаний TE012. В момент резонанса происходит поглощение

Рис. 7.3. Блок-схема установки

энергии электромагнитного поля образцом, что регистрируется СВЧ-

детектором.

Мощность, поглощаемая образцом, очень мала и лишь незначительно превышает уровень шумов. Для увеличения отношения сигнал/шум в установке используется метод синхронного (фазового) детектирования. Метод заключает-

ся в том, что медленно изменяющееся магнитное поле H модулируется высо-

кочастотным магнитным полем с частотой 975 кГц и амплитудой, в несколько раз меньшей полуширины линии поглощения. В результате при резонансе на СВЧ-детекторе выделяется напряжение с частотой, равной частоте модуляции.

50