2.3. Балки и опоры. Реакции и их вычисление

Балками будем называть прямолинейные стержни, работающие на изгиб. В сопротивлении материалов термин «балка» значительно шире, чем в обычном употреблении этого слова: с точки зрения расчета на прочность, жесткость и устойчивость балкой является не только строительная балка, но также и вал, болт, ось железно­дорожного вагона, зуб шестерни и т. д.

Вначале ограничимся построением эпюр для простейшего случая изгиба балок, при котором все заданные нагрузки лежат в одной плоскости, называемой силовой (на рис. 4, а — плоскость П), при­чем эта плоскость совпадает с одной из главных плоскостей балки. Такой слу­чай будем называть плоским изгибом.

На расчетной схеме балку принято заменять ее осью (рис. 4, б). При этом все нагрузки, естественно, должны

Рис 4 быть приведены к оси балки и силовая плос­кость будет совпадать с плоскостью чер­тежа.

Как правило, балки имеют опорные устройства — опоры. Для расчета же их схематизи­руют в виде трех основных типов опор:

а) шарнирно-подвижная опора (рис. 5, а), в которой может возникать только одна составляющая реакции — , направленная вдоль опорного стерженька;

б) шарнирно-неподвижная опора (рис. 5, б), в которой могут возникать две составляющие — вертикальная реакция и гори­зонтальная реакция

в) защемление (иначе жесткое защемление или заделка), где могут быть три составляющие — вертикальная и горизонтальная реакции и опорный момент Ма (рис. 5, в).

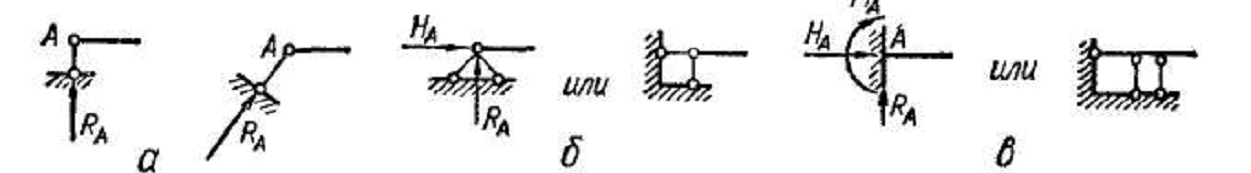
Рис 5

Все реакции и моменты считаются приложенными в точке А — центре тяжести опорного сечения.

Балка, показанная на рис. 6, с, называется простой, или однопролетной , или двухопорной, а расстояние l между опорами — пролетом.

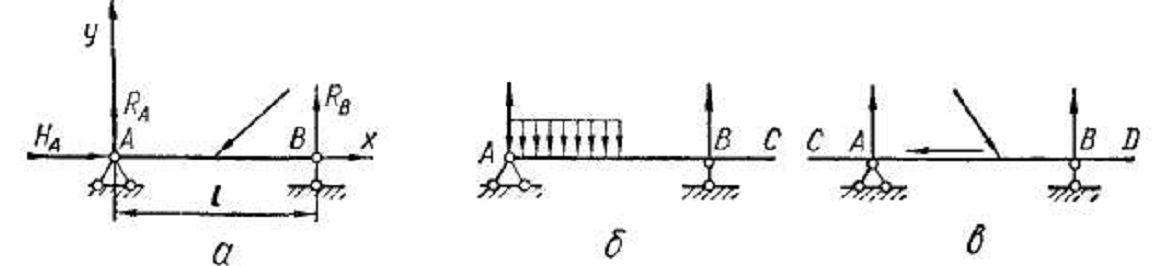
Рис 6

Консолью называется балка, защемленная одним концом и не имеющая других опор (рис. 4, б), или часть балки, свешивающаяся за опоры (часть ВС на рис. 6, б; части АС и BD на рис. 6, е). Бан­ки, имеющие свешивающиеся части, называют консольными (рис. 6, б, в).

Для плоской системы сил можно составить три уравнения статики для определения неизвестных реакций.

Поэтому балка будет статически определимой, если число неизвестных опор­ных реакций не превышает трех; в противном случае балка стати­чески неопределима. Очевидно, что балки, изображенные на рис. 4 и 6, статически определимы.

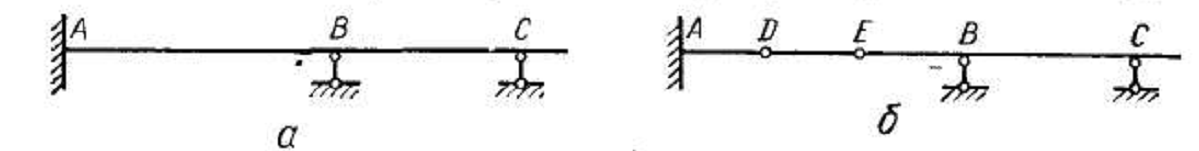
Рис 7

Балка, изображенная на рис. 7, а, называется неразрезной и яв­ляется статически неопределимой, поскольку имеет пять неизвестных опорных реакций: три в опоре А и по одной в опорах В и С.

Поставив в сечениях балки шарниры, например в точках D и Е (рис. 7, б), получим статически определимую шарнирную балку, ибо каждый такой промежуточный шарнир к трем основным уравнениям статики прибавляет одно дополнительное уравнение: сумма моментов относительно центра шарнира от всех сил, расположен­ных по одну сторону от него, равна нулю.

Построение эпюр для статически неопределимых балок требует умения вычислять деформации, а поэтому ограничимся пока исклю­чительно статически определимыми балками.

Способы определения опорных реакций изучают в курсе теоре­тической механики. Поэтому здесь остановимся только на некоторых практических вопросах. Для этого рассмотрим простую балку (рис. 6, а).

1. Опоры обычно обозначают буквами А и В. Три неизвестные реакции находят из следующих уравнений равновесия:

а) сумма проекций всех сил на ось балки равна нулю: откуда находят

б) сумма моментов всех сил относительно опорного шарнира А равна нулю: откуда находят .

в) сумма моментов всех сил относительно опорного шарнира В равна нулю:

откуда находят .

2. Для контроля можно использовать или условие равенства нулю суммы проекций на вертикаль:

или условие равенства нулю суммы моментов относительно какой-либо точки С, отличной от А и В, т. е.

У

Условием пользоваться проще, но оно дает надежную про­верку только в тех случаях, когда к балке не приложены сосредо­точенные моменты.

3. Перед составлением уравнений равновесия нужно выбрать (вообще говоря, произвольно) направления реакций и изобразить их на рисунке. Если в результате вычислений какая-либо реакция получается отрицательной, нужно изменить на рисунке ее направ­ление на обратное и в дальнейшем считать эту реакцию положи­тельной,

5. Если на балку действует распре деленная нагрузка, то для определения реакций ее заменяют равнодействующей, которая равна площади эпюры нагрузки и приложена в центре тя­жести этой эпюры.

Пример 5. Вычислить опорные реакции для балки, показанной на рис. 8.

Прежде всего находим равнодействующие Р₁ и Р₂ нагрузок, распределенных на участках АС н СВ:

; .

Сила Р₁ приложена в центре тяжести прямоугольника, а Р₂ — в центре тяжести треугольника. Находим реакции:

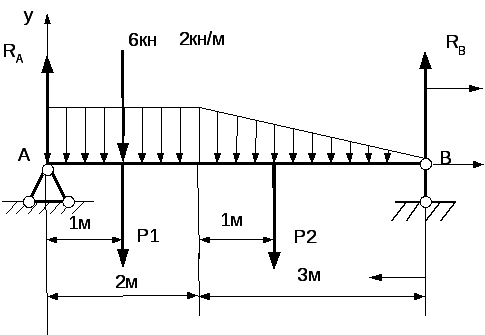
Рис 8

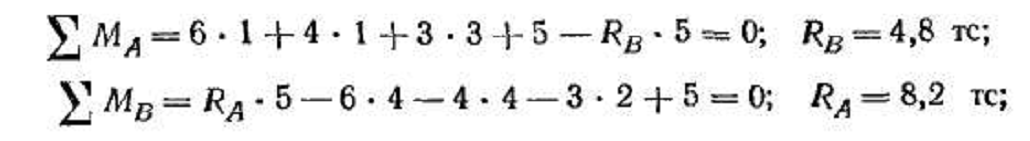
Проверка: