
- •Вопросы к экзамену для ба 4 (озо) модели и методы принятия решений
- •Вопрос 1. Основные понятия теории принятия решений. Современный этап развития теории принятия решений.
- •Вопрос 2. Графы. Способы задания графов.
- •Вопрос 3. Задача о максимальном потоке на сети. Теорема Форда-Фалкерсона. Алгоритм Форда нахождения максимального потока.
- •Вопрос 4. Задача о потоке минимальной стоимости. Алгоритм Басакера-Гоуэна нахождения оптимального потока.
- •Вопрос 5. Задача о кратчайшем маршруте и метод ее решения.
- •Вопрос 6. Метод потенциалов для решения транспортной задачи в сетевой постановке.
- •7. Основные понятия динамического программирования. Задачи, приводящие к динамическому программированию.
- •Вопрос 9. Основные понятия динамического программирования Задача о выборе кратчайшего пути .
- •Вопрос 10. Основные понятия динамического программирования. Планирование производственной программы.
- •Вопрос 11. Основные понятия динамического программирования. Задача об оптимальном распределении ресурсов
- •Вопрос 12. Основные понятия динамического программирования. Задача о замене оборудования.
- •Вопрос 13. Методы векторной оптимизации. Метод последовательных уступок.
- •Вопрос 14. Методы векторной оптимизации. Метод ведущего критерия.
- •Вопрос 11. Методы векторной оптимизации. Метод равных и наименьших отклонений
- •Вопрос 16 Методы векторной оптимизации. Метод минимакса
Вопрос 4. Задача о потоке минимальной стоимости. Алгоритм Басакера-Гоуэна нахождения оптимального потока.
Пусть
задана сеть G(V,
E),
в которой каждой ее дуге приписаны 2
значения: пропускная способность
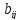 и
и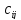 – стоимость доставки единицы потока
по дуге
– стоимость доставки единицы потока
по дуге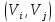 .
Требуется найти поток заданной величиныB
из источника
.
Требуется найти поток заданной величиныB
из источника
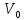 в
сток
в
сток
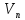 минимальной стоимости. Под стоимостью
потока будем понимать стоимость доставки
того или иного количества вещества из
источника в сток.
минимальной стоимости. Под стоимостью
потока будем понимать стоимость доставки
того или иного количества вещества из
источника в сток.
Математическая модель задачи имеет вид:

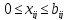
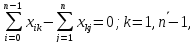
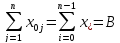
Путь минимальной стоимости – это путь, у которого сумма стоимостей, приписанных дугам, является минимальной. Можно последовательно находить различные пути минимальной стоимости и пропускать потоки по ним до тех пор, пока суммарная величина потока по всем путям не будет равна заданной величине B. На этой идее основан алгоритм Басакера-Гоуэна:
Полагаем все дуговые потоки и величину потока на сети равной 0.
Находим путь минимальной стоимости
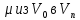 ,
используя стоимости, приписанные дугам
на предыдущей итерации.
,
используя стоимости, приписанные дугам
на предыдущей итерации.Определяем пропускную способность
 найденного пути
найденного пути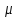
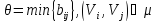
Определяем величину потока
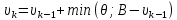 ,
где k
– текущая итерация.
,
где k
– текущая итерация.
Если
получим, что величина
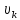 =
= ,
то переходим к заключительному этапу,
иначе – продолжаем алгоритм.
,
то переходим к заключительному этапу,
иначе – продолжаем алгоритм.
Находим величину потока по каждой дуге, принадлежащей найденному пути
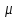 :
:
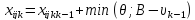 .
.
Пропускные
способности дуг, симметричных дугам
пути
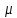 полагаем равными величинам соответствующим
дуговых потоков.
полагаем равными величинам соответствующим
дуговых потоков.
Определяем модифицированные дуговые стоимости
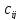 по формуле
по формуле
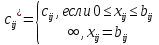
Если
для какой-то дуги
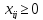 ,
то модифицированная стоимость симметричной
ей дуги равна величине
,
то модифицированная стоимость симметричной
ей дуги равна величине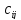 ,
взятой с обратным знаком. Возвращаемся
к 1-му этапу.
,
взятой с обратным знаком. Возвращаемся
к 1-му этапу.
Заключительный этап:
вычисляем
величину стоимости потока по формуле
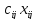 .
.
Пример
5:
Найти поток из вершины
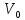 в
вершину
в
вершину
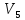 величины B=3
на сети, представленной на рисунке 8,
обладающий минимальной стоимостью.
Первое число, приписанное каждому ребру,
означает пропускную способность, второе
– стоимость доставки единицы потока
по ребру из одной вершины в другую.
Доставка по любому ребру может
осуществляться в любом направлении.
величины B=3
на сети, представленной на рисунке 8,
обладающий минимальной стоимостью.
Первое число, приписанное каждому ребру,
означает пропускную способность, второе
– стоимость доставки единицы потока
по ребру из одной вершины в другую.
Доставка по любому ребру может
осуществляться в любом направлении. 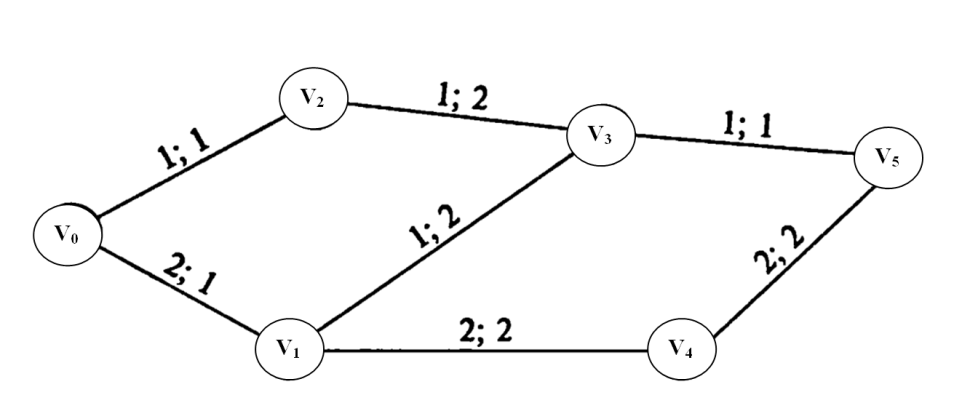
Рисунок 8
Считаем,
что все xij=0,
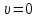
Итерация 1
Применяя алгоритм нахождения кратчайшего пути, определяем, что минимальная стоимость доставки единицы потока из источника в сток равна 4 и достигается по путям:
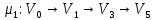
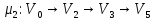
Определяем пропускные способности
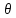 найденных путей и величину потока
найденных путей и величину потока
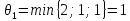
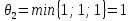
Выберем
для рассмотрения путь
 .
.
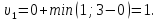
Определяем величины потоков по дугам сети и пропускные способности дуг, симметричных дугам пути:
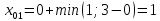
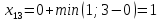
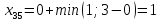
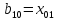
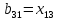
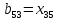
Определяем модифицированные стоимости дуг пути по формуле
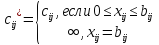
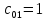 ,
,

Итерация 2
Применяя алгоритм нахождения кратчайшего пути, определяем, что минимальная стоимость доставки единицы потока из источника в сток равна 4 и достигается по путям:
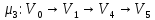
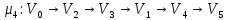
Определяем пропускные способности
 найденных путей и величину потока
найденных путей и величину потока
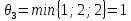
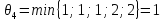
В
этом случае поток пропускаем сразу по
2 путям, так как пропускные способности
общих дуг
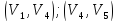 равны 2 единицам. Сумма
равны 2 единицам. Сумма

Следовательно, переходим к заключительному этапу.
Находим стоимость потока
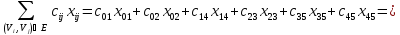
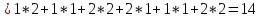
При
этом потоки по дугам
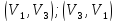 взаимно
погашаются.
взаимно
погашаются.
