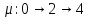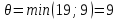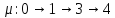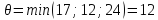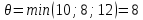- •Вопросы к экзамену для ба 4 (озо) модели и методы принятия решений
- •Вопрос 1. Основные понятия теории принятия решений. Современный этап развития теории принятия решений.
- •Вопрос 2. Графы. Способы задания графов.
- •Вопрос 3. Задача о максимальном потоке на сети. Теорема Форда-Фалкерсона. Алгоритм Форда нахождения максимального потока.
- •Вопрос 4. Задача о потоке минимальной стоимости. Алгоритм Басакера-Гоуэна нахождения оптимального потока.
- •Вопрос 5. Задача о кратчайшем маршруте и метод ее решения.
- •Вопрос 6. Метод потенциалов для решения транспортной задачи в сетевой постановке.
- •7. Основные понятия динамического программирования. Задачи, приводящие к динамическому программированию.
- •Вопрос 9. Основные понятия динамического программирования Задача о выборе кратчайшего пути .
- •Вопрос 10. Основные понятия динамического программирования. Планирование производственной программы.
- •Вопрос 11. Основные понятия динамического программирования. Задача об оптимальном распределении ресурсов
- •Вопрос 12. Основные понятия динамического программирования. Задача о замене оборудования.
- •Вопрос 13. Методы векторной оптимизации. Метод последовательных уступок.
- •Вопрос 14. Методы векторной оптимизации. Метод ведущего критерия.
- •Вопрос 11. Методы векторной оптимизации. Метод равных и наименьших отклонений
- •Вопрос 16 Методы векторной оптимизации. Метод минимакса
Вопрос 3. Задача о максимальном потоке на сети. Теорема Форда-Фалкерсона. Алгоритм Форда нахождения максимального потока.
Сеть
– это ориентированный граф G(V,
E)
без контуров, дугам или вершинам которого
приписаны некоторые числовые значения.
Будем полагать, что она является
симметрическим графом, каждая вершина
которого
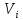 характеризуется таким параметром, какинтенсивность
характеризуется таким параметром, какинтенсивность
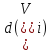 .
При этом вершина, для которой
.
При этом вершина, для которой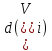 >0
называетсяистоком
(источником) V0.
Вершина, для которой
>0
называетсяистоком
(источником) V0.
Вершина, для которой
 0
называетсястоком
Vn,
все остальные вершины – промежуточные.
Будем рассматривать сети с единственным
источником и единственным стоком.
0
называетсястоком
Vn,
все остальные вершины – промежуточные.
Будем рассматривать сети с единственным
источником и единственным стоком.
По
путям сети из источника в сток направляется
однородное вещество (газ, жидкость и т.
п.) транспорт и т. д. Каждая дуга сети
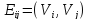 обладаетпропускной
способностью
обладаетпропускной
способностью
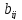 – максимальное количество вещества,
которое дуга может пропустить за единицу
времени.Поток
– максимальное количество вещества,
которое дуга может пропустить за единицу
времени.Поток
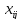 по дуге
по дуге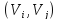 равен фактическому количеству вещества,
перемещаемому по ней в единицу времени.
Совокупность потоков по всем дугам сети
называется потоком
из источника в сток.
равен фактическому количеству вещества,
перемещаемому по ней в единицу времени.
Совокупность потоков по всем дугам сети
называется потоком
из источника в сток.
Если пропускные способности симметричных дуг равны между собой, то эти дуги могут быть заменены ребрами. Поэтому задача о максимальном потоке на сети имеет место и для смешанных и неориентированных графов. Сформулируем математическую модель задачи:
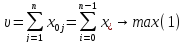
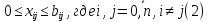
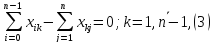
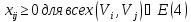
Целевая функция (1) имеет такой вид, так как максимальный поток равен количеству вещества, вытекающего из источника, и равен количеству вещества, притекающего в сток.
Условие (2) ограничивает поток по всем дугам сети их пропускными способностями.
Условие (3) обеспечивает равенство количества вещества, притекающего в любую промежуточную вершину, количеству вещества, вытекающего из нее.
Условие (4) следует из здравого смысла задачи.
Разобьем
множество V
вершин
сети на 2 непересекающихся подмножества
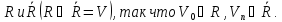
Разрезом,
отделяющим
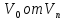 ,
называют совокупность всех дуг
,
называют совокупность всех дуг
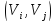 ,
таких что
,
таких что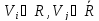 .
.
Пропускная способность разреза равна сумме пропускных способностей дуг, его образующих.
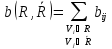
Так
как пропускная способность пути равна
наименьшей из пропускных способностей
дуг, входящих в этот путь, то величина
потока, перемещаемого по всем возможным
путям сети, соединяющим источник со
стоком, не может превышать пропускной
способности любого разреза сети, т. е.
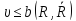 .
.
Теорема
Форда-Фалкерсона:
В
любой сети максимальная величина потока
из источника
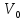 в
сток
в
сток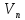 равна
минимальной пропускной способности
разреза, отделяющего источник
равна
минимальной пропускной способности
разреза, отделяющего источник
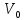 от стока
от стока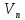 .
.
Алгоритм Форда:
Предварительный шаг: создание таблицы пропускных способностей
Записываем пропускные способности дуг сети в матрицу B (n+1)× (n+1) (порядок квадратной матрицы равен количеству вершин сети) по принципу:
если
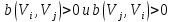 ,
то
,
то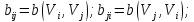
если
 ,
то
,
то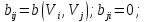
если
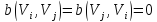 ,
то элементы
,
то элементы не заполняем.
не заполняем.
Основной
шаг: нахождение пути из источника
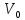 в
сток
в
сток
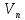 с положительной проспускной способностью
с положительной проспускной способностью
0 столбец, соответствующий источнику, помечаем *. Отыскиваем в 0-ой строке таблицы положительные элементы и столбцы, в которых они находятся, помечаем сверху номером просматриваемой строки (т. е. цифрой 0). В результате выделенными окажутся дуги, которые могут служить первыми дугами пути из
 в
в
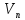 .
.Далее просматриваем те строки, номера которых совпадают с номерами помеченных столбцов. В каждой такой строке находим положительные элементы в непомеченных столбцах, и помечаем эти столбцы номером просматриваемой строки. Продолжаем аналогичный просмотр до тех пор, пока:
А)
не будет отмечен сток
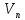 – найден путь из
– найден путь из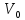 в
в
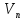 с положительной пропускной способностью;
с положительной пропускной способностью;
Б)
либо уже нельзя пометить новые столбцы
– нет пути
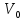 в
в
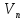 .
.
Случай А.
А-1)
Находим искомый путь
 от конца к началу. Для этого смотрим,
какой цифрой помечен столбец стока
от конца к началу. Для этого смотрим,
какой цифрой помечен столбец стока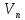 – это номер начальной вершины последней
дуги в найденном пути. Далее смотрим,
какой цифрой отмечен столбец этой
вершины, и так далее, пока не доберемся
до источника.
– это номер начальной вершины последней
дуги в найденном пути. Далее смотрим,
какой цифрой отмечен столбец этой
вершины, и так далее, пока не доберемся
до источника.
А-2)
Находим пропускную способность
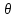 найденного пути
найденного пути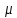 как наименьшую пропускную способность
дуг, входящих в этот путь
как наименьшую пропускную способность
дуг, входящих в этот путь
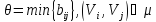
А-3)
Определяем остаточные пропускные
способности дуг найденного пути и
симметричным к ним. Для этого из элементов
таблицы
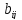 вычтем
вычтем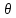 ,
а к элементам
,
а к элементам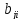 добавим
добавим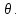
В результате получим таблицу, аналогичную исходной, для которой снова запускаем основной шаг алгоритма Форда. И так до тех пор, пока не придем к случаю Б).
Случай Б.
Вершины,
находящиеся в помеченных столбцах
таблицы, образуют подмножество
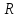 ,
все оставшиеся вершины –
,
все оставшиеся вершины –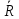 .
Таким образом, получен разрез с минимальной
пропускной способностью.
.
Таким образом, получен разрез с минимальной
пропускной способностью.
Заключительный
шаг: определение величины максимального
потока на сети. Для
этого из элементов исходной таблицы
вычитаем соответствующие элементы
последней таблицы, полученной на основном
шаге алгоритма. В результате получим
таблицу, положительные элементы которой
– величины потоков
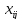 по соответствующим дугам. А максимальный
поток на сети – сумма элементов 0-ой
строки илиn-го
столбца.
по соответствующим дугам. А максимальный
поток на сети – сумма элементов 0-ой
строки илиn-го
столбца.

Пример
3.
Найти максимальный поток из
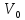 в
в
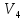 на сети, изображенной на рисунке 5.
на сети, изображенной на рисунке 5.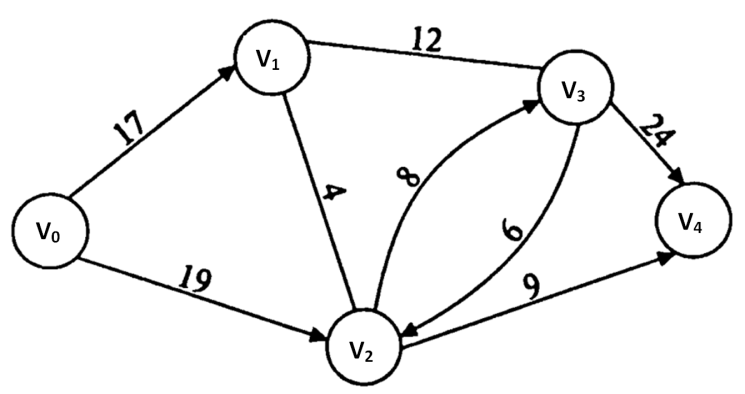
Рисунок 5
Заметим,
что данный граф является смешанным: (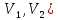 ,
(
,
(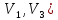 изображены как ребра. Это значит, что
дуги (
изображены как ребра. Это значит, что
дуги (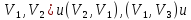 (
( являются симметрическими с равными
пропускными способностями, т.е.
являются симметрическими с равными
пропускными способностями, т.е.
(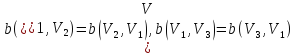 .
.
Предварительный шаг алгоритма Форда:
Формируем матрицу пропускных способностей
|
|
0 |
1 |
2 |
3 |
4 |
|
0 |
|
17 |
19 |
|
|
|
1 |
0 |
|
4 |
12 |
|
|
2 |
0 |
4 |
|
8 |
9 |
|
3 |
|
12 |
6 |
|
24 |
|
4 |
|
|
0 |
0 |
|
Основной шаг:
Таблица 1
|
|
0* |
10 |
20 |
31 |
42
|
|
0 |
|
17 |
19 |
|
|
|
1 |
0 |
|
4 |
12 |
|
|
2 |
0 |
4 |
|
8 |
9 |
|
3 |
|
12 |
6 |
|
24 |
|
4 |
|
|
0 |
0 |
|
Таблица 2
|
|
0* |
10 |
20 |
31 |
43
|
|
0 |
|
17 |
10 |
|
|
|
1 |
0 |
|
4 |
12 |
|
|
2 |
9 |
4 |
|
8 |
0 |
|
3 |
|
12 |
6 |
|
24 |
|
4 |
|
|
9 |
0 |
|
Таблица 3
|
|
0* |
10 |
20 |
32 |
43
|
|
0 |
|
5 |
10 |
|
|
|
1 |
12 |
|
4 |
0 |
|
|
2 |
9 |
4 |
|
8 |
0 |
|
3 |
|
24 |
6 |
|
12 |
|
4 |
|
|
9 |
12 |
|
Таблица 4
Нельзя
отметить новые столбцы. Нет пути из
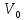 в
в
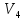 .
.
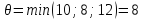
Разрез
с минимальной пропускной способностью
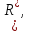
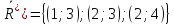
|
|
0* |
10 |
20 |
3 |
4 |
|
0 |
|
5 |
2 |
|
|
|
1 |
12 |
|
4 |
0 |
|
|
2 |
17 |
4 |
|
0 |
0 |
|
3 |
|
24 |
14 |
|
4 |
|
4 |
|
|
9 |
20 |
|
Заключительный шаг:
|
|
0 |
1 |
2 |
3 |
4 |
|
0 |
|
12 |
17 |
|
|
|
1 |
-12 |
|
0 |
12 |
|
|
2 |
-17 |
0 |
|
8 |
9 |
|
3 |
|
-12 |
-8 |
|
20 |
|
4 |
|
|
-9 |
-20 |
|
Дуговые потоки: х01=12, х02=17, х13=12, х23=8, х24=9, х34=20.
Максимальный
поток равен сумме элементов 0-ой строки
или сумме элементов 0-го столбца:
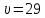 .
.
Проверим теорему Форда-Фалкерсона:
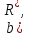
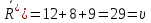 .
.
Все верно.