Вопрос 2. Графы. Способы задания графов.

Теория графов – это раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами. Как прикладная дисциплина теория графов позволяет описывать и исследовать многие технические, экономические, биологические и социальные системы.

Графы возникли в восемнадцатом столетии, когда известный математик, Леонард Эйлер, пытался решить теперь уже классическую задачу о Кенигсбергских мостах. В то время в городе Кенигсберге было два острова, соединенных семью мостами с берегами реки Преголь и друг с другом так, как показано на рисунке 1.

Рисунок 1

Задача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя ровно по одному разу по каждому мосту, вернуться в то же место, откуда начиналась прогулка. Решая эту задачу, Эйлер изобразил Кенигсберг в виде графа (рисунок 2), отождествив его вершины с частями города, а ребра — с мостами, которыми связаны эти части.

Рисунок 2

Эйлеру удалось доказать, что искомого пути обхода города не существует.

Математически графом G(V, E) называют совокупность двух множеств: непустого множества V – множества вершин и множества Е – пар элементов из V. Например, G(V, E) V = {a, b, c, d}, E = {(a, b), (a, c),(a, d), (d, c)}.

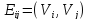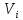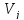Если элементы множества Е не упорядочены, то они называются ребрами, а граф – неориентированным. Если же элементы множества Е упорядочены, то они называются дугами, а граф – ориентированным или орграфом. Граф называется смешанным, если его вершины соединяются, как ребрами, так и дугами. Говорят, что ребро соединяет вершиныи, а дуга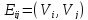начинается в вершине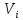и заканчивается в вершине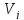(исходит из вершиныи заходит в вершину).

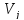На бумаге или экранах ЭВМ вершины графа изображаются точками или кружками, ребра – линиями, дуги – линиями со стрелками, где стрелка указывает на вторую вершину в упорядоченной паре вершин.

Орграф называется симметрическим, если для любой дуги 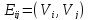из множестваЕ дуга 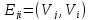также принадлежит множествуЕ. И антисимметрическим, если для любой дуги из множестваЕ дуга 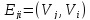не принадлежит множествуЕ. Любой симметрический орграф можно рассматривать как неориентированный граф, в котором каждому ребру соответствует пара симметрических дуг орграфа.

В неориентированном графе вершины, являющиеся концевыми точками одного ребра, называются смежными вершинами. В орграфе вершина является смежной с вершиной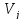, если есть дуга, исходящая из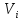и входящая в.

При этом смежные вершины инцидентны этому ребру (дуге), также как и ребро (дуга) инцидентно этим вершинам.

2 ребра называются смежными, если они инцидентны одной и той же вершине графа. Ребра, инцидентные одной и той же паре вершин, называются кратными ребрами. 2 дуги называются смежными, если конечная вершина одной дуги является начальной вершиной другой дуги.

Ребро (дуга), начинающееся и заканчивающееся в одной вершине, называются петлей.

Число ребер, инцидентных вершине неориентированного графа V_i, называется степенью или валентностью вершины V_i и обозначается ρ(V_i).

Для вершины V_i ориентированного графа определяют полустепень исхода ρ(V_i^>) как количество дуг, исходящих из этой вершины, и полустепень захода ρ(V_i^<) как количество дуг, входящих в эту вершину. Степенью вершины орграфа V_i называется сумма ее полустепеней исхода и захода.

ρ(V_i)= ρ(V_i^>)+ ρ(V_i^<)

Вершина степени 1 называется висячей, а степени 0 – изолированной.

Путь в графе – последовательность вершин V_i, в которой 2 любые соседние вершины соединены, по крайней мере, одним ребром (дугой).

Путь формирует цикл, если начальная и конечная вершина пути совпадают.

Контур – это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней.

Существует несколько способов матричного задания графов:

• Матрица смежности вершин

• Матрица смежности ребер (дуг)

• Матрица инцидентности.

Матрица смежности вершин одинаково определяется для ориентированного и неориентированного графов. Матрица смежности вершин – это квадратная матрица А порядка n, где n – число вершин, элементы которой задаются по формуле:

,

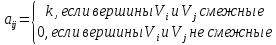где k – количество ребер, соединяющих вершины 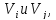или количество дуг, идущих из вершиныв вершину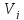для орграфа.

В случае неориентированного графа матрица смежности вершин является симметрической. Верно и обратное: любая симметрическая матрица с неотрицательными элементами может быть интерпретирована как граф.

Матрица смежности ребер (дуг) – это квадратная матрица А порядка m, где m – число ребер (дуг), элементы которой задаются по формуле:

,

где k – количество ребер, соединяющих вершины 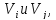или количество дуг, идущих из вершины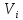в вершину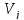для орграфа.

Матрица инцидентности ориентированного графа – это прямоугольная матрица А порядка n×m, где n – число вершин, m – число дуг, элементы которой задаются по формуле:

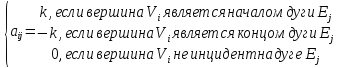
где k –количество дуг, идущих из вершины в вершину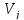для орграфа.

Матрица инцидентности неориентированного графа – это прямоугольная матрица А порядка n×m, где n – число вершин, m – число ребер, элементы которой задаются по формуле:

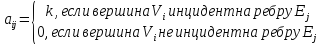
где k – количество ребер, соединяющих вершины .

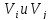Пример 1. Представить ориентированный граф на рисунке 3 в виде матриц смежности вершин и дуг и матрицы инцидентности.

Рисунок 3

Матрица смежности вершин для графа на рисунке 3

	1	2	3	4
1	0	0	0	1
2	0	0	0	0
3	0	1	0	0
4	0	1	1	0

Матрица смежности дуг для графа на рисунке 3

	(1,4)	(3,2)	(4,2)	(4,3)
(1,4)	0	0	1	1
(3,2)	0	0	0	0
(4,2)	0	0	0	0
(4,3)	0	1	0	0

Матрица инцидентности для графа на рисунке 3

	(1,4)	(3,2)	(4,2)	(4,3)
1	1	0	0	0
2	0	–1	–1	0
3	0	1	0	–1
4	–1	0	1	1

Пример 2. Представить неориентированный граф на рисунке 4 в виде матриц смежности вершин и ребер и матрицы инцидентности.

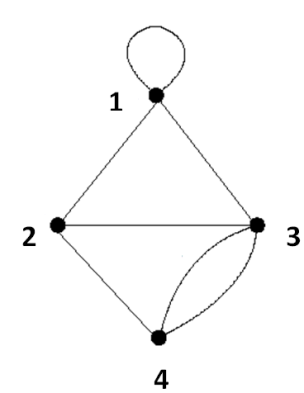
Рисунок 4

Матрица смежности вершин для графа на рисунке 4

	1	2	3	4
1	1	1	1	0
2	1	0	1	1
3	1	1	0	2
4	0	1	2	0

Матрица смежности ребер для графа на рисунке 4

	(1,1)	(1,2)	(1,3)	(2,3)	(2,4)	(3,4)
(1,1)	1	1	1	0	0	0
(1,2)	1	1	1	1	1	0
(1,3)	1	1	1	1	0	1
(2,3)	0	1	1	1	1	1
(2,4)	0	1	0	1	1	1
(3,4)	0	0	1	1	1	2

Матрица инцидентности для графа на рисунке 4

	(1,1)	(1,2)	(1,3)	(2,3)	(2,4)	(3,4)
1	1	1	1	0	0	0
2	0	1	0	1	1	0
3	0	0	1	1	0	2
4	0	0	0	0	1	2