
- •Вопросы к экзамену для ба 4 (озо) модели и методы принятия решений
- •Вопрос 1. Основные понятия теории принятия решений. Современный этап развития теории принятия решений.
- •Вопрос 2. Графы. Способы задания графов.
- •Вопрос 3. Задача о максимальном потоке на сети. Теорема Форда-Фалкерсона. Алгоритм Форда нахождения максимального потока.
- •Вопрос 4. Задача о потоке минимальной стоимости. Алгоритм Басакера-Гоуэна нахождения оптимального потока.
- •Вопрос 5. Задача о кратчайшем маршруте и метод ее решения.
- •Вопрос 6. Метод потенциалов для решения транспортной задачи в сетевой постановке.
- •7. Основные понятия динамического программирования. Задачи, приводящие к динамическому программированию.
- •Вопрос 9. Основные понятия динамического программирования Задача о выборе кратчайшего пути .
- •Вопрос 10. Основные понятия динамического программирования. Планирование производственной программы.
- •Вопрос 11. Основные понятия динамического программирования. Задача об оптимальном распределении ресурсов
- •Вопрос 12. Основные понятия динамического программирования. Задача о замене оборудования.
- •Вопрос 13. Методы векторной оптимизации. Метод последовательных уступок.
- •Вопрос 14. Методы векторной оптимизации. Метод ведущего критерия.
- •Вопрос 11. Методы векторной оптимизации. Метод равных и наименьших отклонений
- •Вопрос 16 Методы векторной оптимизации. Метод минимакса
Вопрос 16 Методы векторной оптимизации. Метод минимакса
В
методе минимакса сначала решается
исходная задача по каждому из критериев
в отдельности и находятся их значения
 .Дадим
обоснование функции и дополнительных
ограничений в этом методе.
.Дадим
обоснование функции и дополнительных
ограничений в этом методе.
Используя
найденные значения функций
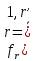 ,
найдем их относительные отклонения
от показателей функций в компромиссном
решении:
,
найдем их относительные отклонения
от показателей функций в компромиссном
решении:
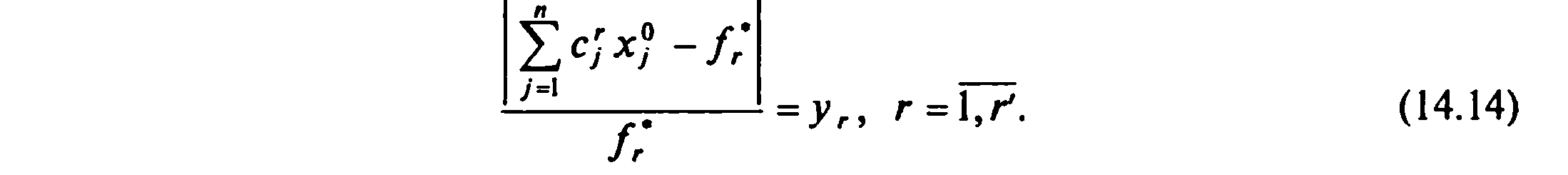
Здесь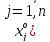 —
значения компонентов в компромиссном
решении. Выделим из полученных
отклонений наибольшее и потребуем,
чтобы в искомом компромиссном решении
оно было минимальным. Тогда функция в
общем виде запишется так:
—
значения компонентов в компромиссном
решении. Выделим из полученных
отклонений наибольшее и потребуем,
чтобы в искомом компромиссном решении
оно было минимальным. Тогда функция в
общем виде запишется так:

Из
выражения (14.15) и вытекает название —
метод минимакса. Заменим в (14.14) отдельные
отклонения
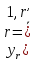 наибольшим из них, обозначив его
наибольшим из них, обозначив его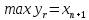 ,
тогда получим нестрогие неравенства
,
тогда получим нестрогие неравенства

Умножим
выражения (14.16) на их знаменатель, отчего
смысл их не нарушится, так как в
практических задачах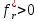 .
.
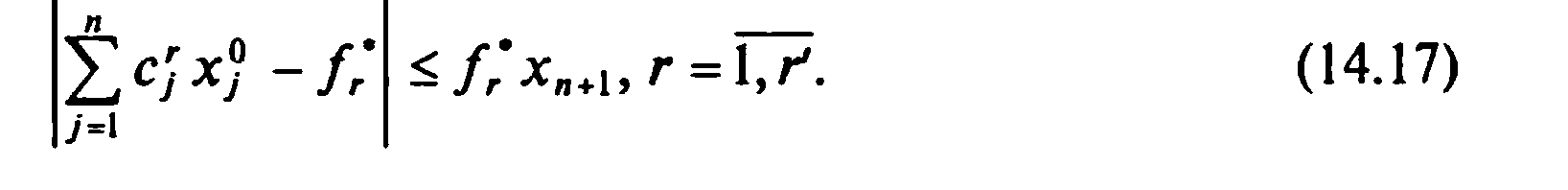
Учитывая, что в компромиссном решении значение максимизируемого критерия меньше его экстремального значения, а величина минимизируемого критерия больше соответствующего экстремального значения, имеем:
для максимизируемых критериев
![]()
При снятии знака модуля с левой части (14.17) получим
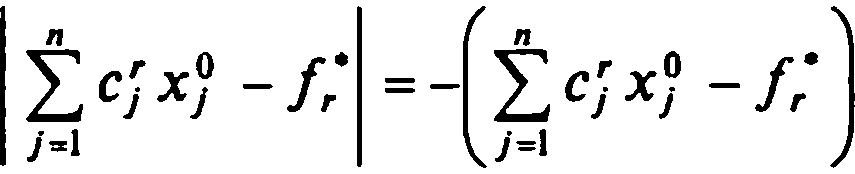
С учетом этого (14.17) запишем в виде

для минимизируемых критериев
![]()
тогда снятие знака модуля не требует преобразований и (14.17) запишется в виде
![]()
Поскольку
компромиссное решение нами не определено,
а следовательно, неизвестные величины
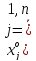 и значение
новой неизвестной
и значение
новой неизвестной
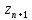 не
найдены, то будем считать величины
не
найдены, то будем считать величины неизвестными
неизвестными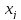 .
Тогда для нахождения компромиссного
решения методом минимакса к исходной
системе ограничений добавим ограничения
вида (14.18):
.
Тогда для нахождения компромиссного
решения методом минимакса к исходной
системе ограничений добавим ограничения
вида (14.18):
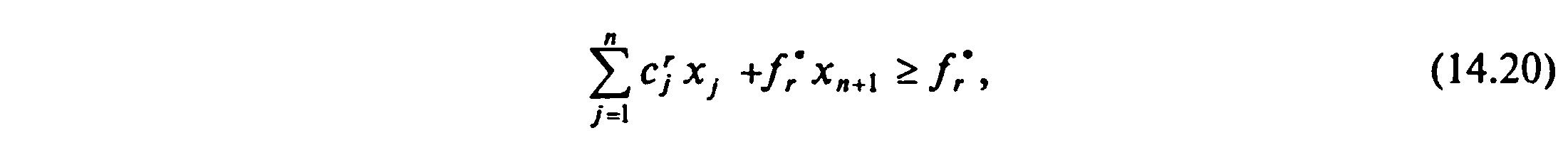
сформированные для всех г, относящихся к максимизируемым критериям, и — вида (14.19):
![]()
сформированные для всех r, относящихся к минимизируемым критериям.
Целевая
функция расширенной задачи с учетом
подстановки
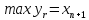 в
выражение (14.15) имеет вид
в
выражение (14.15) имеет вид
![]()
1Заключение, вывод из чего-л., избранный путь действия после обдумывания, обсуждения какого-л. вопроса.
2Брать под свою ответственность.
