- •Вопросы к экзамену для ба 4 (озо) модели и методы принятия решений
- •Вопрос 1. Основные понятия теории принятия решений. Современный этап развития теории принятия решений.
- •Вопрос 2. Графы. Способы задания графов.
- •Вопрос 3. Задача о максимальном потоке на сети. Теорема Форда-Фалкерсона. Алгоритм Форда нахождения максимального потока.
- •Вопрос 4. Задача о потоке минимальной стоимости. Алгоритм Басакера-Гоуэна нахождения оптимального потока.
- •Вопрос 5. Задача о кратчайшем маршруте и метод ее решения.
- •Вопрос 6. Метод потенциалов для решения транспортной задачи в сетевой постановке.
- •7. Основные понятия динамического программирования. Задачи, приводящие к динамическому программированию.
- •Вопрос 9. Основные понятия динамического программирования Задача о выборе кратчайшего пути .
- •Вопрос 10. Основные понятия динамического программирования. Планирование производственной программы.
- •Вопрос 11. Основные понятия динамического программирования. Задача об оптимальном распределении ресурсов
- •Вопрос 12. Основные понятия динамического программирования. Задача о замене оборудования.
- •Вопрос 13. Методы векторной оптимизации. Метод последовательных уступок.
- •Вопрос 14. Методы векторной оптимизации. Метод ведущего критерия.
- •Вопрос 11. Методы векторной оптимизации. Метод равных и наименьших отклонений
- •Вопрос 16 Методы векторной оптимизации. Метод минимакса
Вопрос 14. Методы векторной оптимизации. Метод ведущего критерия.
Этот
метод является частным случаем метода
последовательных уступок.
В методе ведущего критерия все
критерии, кроме самого важного, заносятся
в систему ограничений. Умножив все
критерии минимизации функций на (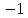 )
и обозначив через
)
и обозначив через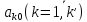 нижние границы соответствующих критериев,
математическую модель задачи можно
записать в виде
нижние границы соответствующих критериев,
математическую модель задачи можно
записать в виде
 (14.1)
(14.1)
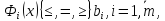 (14.2)
(14.2)
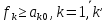 ,
(14.3)
,
(14.3)
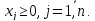 (14.4)
(14.4)
Вопрос 11. Методы векторной оптимизации. Метод равных и наименьших отклонений
Пусть необходимо найти компромиссное решение задачи по к' критериям методом равных и наименьших относительных отклонений, т.е.
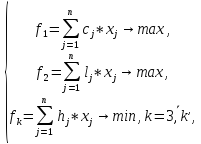 (14.5)
(14.5)
при
ограничениях

Запишем условие равенства относительных отклонений значений критериев от их экстремальных значений для к' критериев:
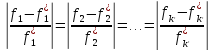 (14.6)
(14.6)
В
выражении (14.6)
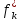 —
экстремальное значение критерия
—
экстремальное значение критерия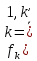 Рассмотрим четыре первых критерия (к'
>
4).
Рассмотрим четыре первых критерия (к'
>
4).
Пусь
в условии задачи критерии
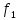 и
и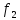 максимизируются,
а
максимизируются,
а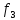 и
и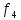 минимизируются.
минимизируются.
Осуществим
анализ числителей относительных
отклонений первых двух критериев. Оба
числителя
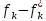 положительны при
положительны при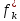 < 0 и отрицательны при
< 0 и отрицательны при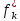 >
0 (k
= 1, 2). Поэтому в равенстве относительных
отклонений этих критериев скобки
абсолютных величин можно опустить, т.е.
для первых двух критериев справедливо
выражение
>
0 (k
= 1, 2). Поэтому в равенстве относительных
отклонений этих критериев скобки
абсолютных величин можно опустить, т.е.
для первых двух критериев справедливо
выражение
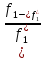 =
=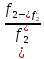 или
или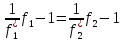 (14.7)
(14.7)
Обозначив
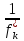 =dk
(k
=1,2) и подставив в (14.7), получим
=dk
(k
=1,2) и подставив в (14.7), получим
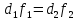 или
или
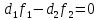 (14.8)
(14.8)
Если рассмотреть третий и четвертый критерии, то для них получим точно такое же уравнение, так как направления их оптимизации совпадают:
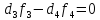
Возьмем
теперь критерии
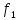 ,
,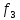 с разными направлениями оптимизации.
с разными направлениями оптимизации.
Для
них при
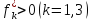
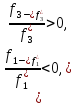
а
при
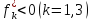
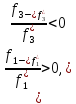 .
.
Из проведенного анализа видно, что знаки выражений в скобках абсолютных величин всегда противоположны, поэтому, опуская скобки абсолютных величин, перед одним из выражений нужно поставить знак минус:
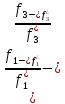 ,
,
или
с учетом обозначения
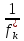 =dk
(k
=1,3) имеем
=dk
(k
=1,3) имеем

Итак, равенство относительных отклонений для любых двух максимизируемых (минимизируемых) критериев имеет вид (14.8), а для любых двух критериев с противоположными направлениями оптимизации — вид (14.9).
Таким образом, для нахождения компромиссного решения методом равных и наименьших относительных отклонений необходимо оптимизируемые критерии включить в число неизвестных задачи и дополнить систему ограничений исходной задачи следующими ограничениями:
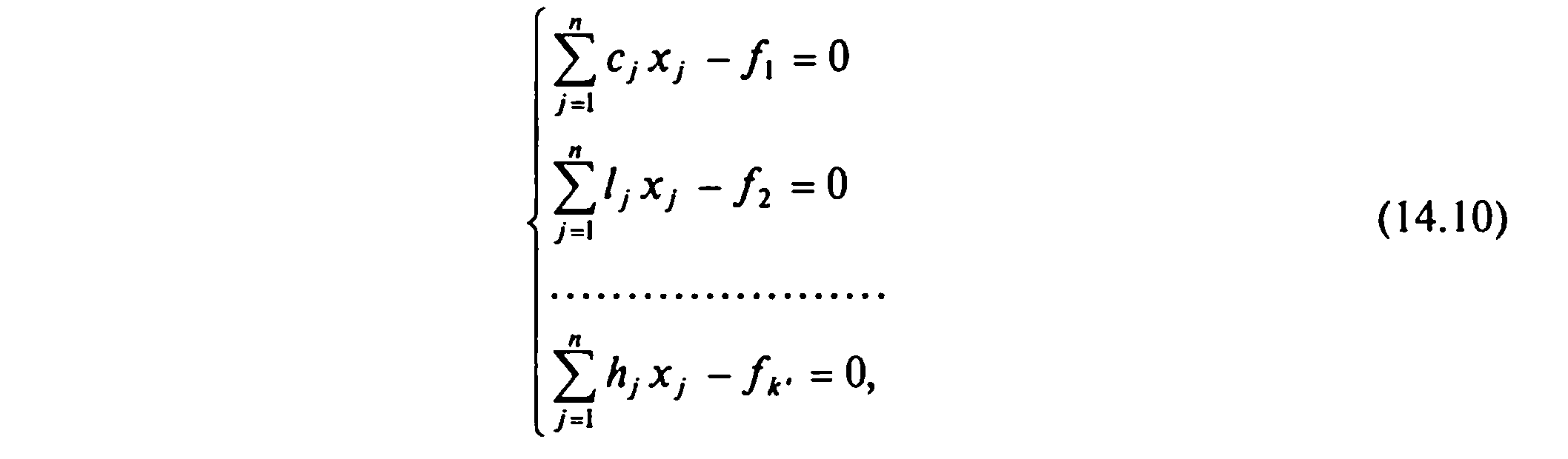
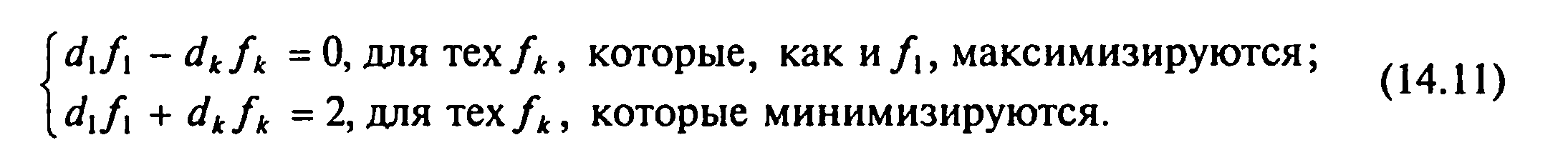
В
качестве целевой функции можно взять
любую из функций
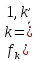 .
.
При
этом следует иметь в виду, что относительное
отклонение максимизируемого критерия
будет наименьшим тогда, когда fk
приблизится к максимальному значению
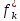 ,
а для минимизируемого критерия
относительное отклонение станет
минимальным, еслиfk
будет приближаться к наименьшему
значению
,
а для минимизируемого критерия
относительное отклонение станет
минимальным, еслиfk
будет приближаться к наименьшему
значению
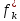 т.е.
т.е.

Отметим, что дополнительных ограничений расширенной задачи вида (14.11) на одно меньше числа критериев.
Если необходимо улучшить значения каких-то критериев, то улучшение оценивается количественно и в условие (14.2) вводятся весовые коэффициенты а2,а3,..., ак. (а1 = 1). Условие равенства относительных отклонений в этом случае будет иметь вид