
1 курс / Kurs_lektsiy_po_fizike_-_1_semestr1
.pdfМ.А.Зеликман
Курс лекций по физике
1-й семестр
Классическая механика. Специальная теория относительности. Механические колебания.
Молекулярная физика и термодинамика.
Учебное пособие
Санкт-Петербург
2015
|
|
ОГЛАВЛЕНИЕ |
|
|||
Векторы и их свойства. |
3 |
Глава 7. Механические колебания. |
|
|||
Механика |
|
|
||||
Глава 1. Кинематика |
|
1. |
Общие положения |
55 |
||
1.Скорость. |
6 |
2. |
Малые колебания. |
55 |
||
2.Ускорение. |
7 |
3. |
Гармонические колебания. |
56 |
||
3. |
Равномерное прямолинейное движение. 9 |
4. |
Маятник. |
57 |
||
4. |
Равноускоренное движение. |
10 |
5. |
Биения. |
58 |
|
5. |
Кинематика вращательного движения. |
11 |
6. |
Затухающие колебания. |
58 |
|
Глава 2. Динамика. |
|
7. |
Вынужденные колебания. |
59 |
||
1. |
Законы Ньютона. |
12 |
8. |
Параметрический резонанс. |
60 |
|
2.Силы в природе |
15 |
9. |
Автоколебания. |
61 |
||
Глава 3. Законы сохранения. |
|
Молекулярная физика и термодинамика |
||||
1.Закон сохранения импульса. |
17 |
1. |
Стат. физика и термодинамика. |
62 |
||
2.Кинетическая энергия. Работа. |
19 |
2. |
Давление. |
62 |
||
3.Потенциальное поле сил. |
20 |
3. |
Распределение давления в покоящихся |
|||
4.Потенциальная энергия во внешнем |
|
|
|
жидкости и газе. |
63 |
|
поле сил. |
21 |
4. |
Закон Архимеда. |
64 |
||
5.Потенциальная энергия взаимодействия.22 |
5. |
Масса и размер молекулы. |
65 |
|||
6.Закон сохранения механической энергии 24 |
6. |
Равновесные и неравновесные |
|
|||
7.Закон сохранения момента импульса. |
24 |
|
процессы. |
65 |
||
Глава 4. Неинерциальные системы отсчета. |
7. |
Внутренняя энергия. |
65 |
|||
1. |
Силы инерции. |
26 |
8. |
Первое начало термодинамики. |
66 |
|
2. |
Центробежная сила инерции. |
27 |
9. |
Работа, совершаемая газом. |
67 |
|
3. |
Сила Кориолиса. |
28 |
10. |
Уравнение состояния идеального газа.67 |
||
Глава 5. Механика твердого тела. |
|
11. |
Внутренняя энергия и теплоемкость |
|
||
1. |
Движение твердого тела. |
30 |
|
|
идеального газа. |
68 |
2. |
Движение центра масс. |
31 |
12. |
Уравнение адиабаты идеального газа.69 |
||
3. |
Вращение тела вокруг неподвижной оси. 32 |
13. |
Политропические процессы. |
69 |
||
4. |
Момент инерции. |
34 |
14. |
Работа, совершаемая идеальным газом |
||
5. |
Кинетическая энергия тела, |
|
|
|
при различных процессах. |
70 |
|
вращающегося вокруг неподвижной оси. 36 |
15. |
Ван-дер-Ваальсовский газ. |
70 |
||
6. |
Кинетическая энергия тела |
|
16. |
Барометрическая формула. |
72 |
|
|
при плоском движении. |
37 |
Статистическая физика |
|
||
7. |
Применение законов |
|
1. |
Некоторые сведения из теории |
|
|
|
динамики твердого тела. |
37 |
|
вероятностей. |
72 |
|
8. |
Пример с цилиндром - 2 способа. |
39 |
2. |
Число ударов молекул о стенку. |
74 |
|
9. |
Закон всемирного тяготения |
40 |
3. |
Давление газа на стенку (основное |
|
|
10. Космические скорости. |
41 |
|
|
уравнение МКТ). |
76 |
|
|
Глава 6. Релятивистская механика. |
|
4. |
Средняя энергия молекул. |
76 |
|
1.Специальная теория |
|
5. |
Распределение Максвелла. |
78 |
||
|
относительности |
42 |
6. |
Опыты Штерна и Ламмерта. |
82 |
|
2. |
Преобразования Лоренца |
45 |
7. |
Распределение Больцмана. |
83 |
|
3. |
Следствия из преобразований Лоренца 46 |
8. |
Макро- и микросостояния. Стат. вес. |
84 |
||
4. |
Парадокс близнецов. |
48 |
9. |
Энтропия. |
87 |
|
5. |
Интервал. |
50 |
10. |
Основные законы термодинамики. |
|
|
6. |
Преобразования Лоренца и сложение |
|
|
|
Тепловые машины. |
89 |
|
скоростей. |
51 |
11. |
Цикл Карно. |
90 |
|
7. |
Релятивистское выражение |
|
12. |
Фазовые равновесия и превращения 92 |
||
|
для импульса |
51 |
13. |
Испарение и конденсация |
92 |
|
8. |
Второй закон Ньютона |
52 |
14. |
Равновесие жидкости и пара |
93 |
|
9. |
Релятивистское выражение |
|
15. |
Критическое состояние |
94 |
|
|
для энергии. |
53 |
16. |
Пересыщенный пар и перегретая |
|
|
9. |
Связь массы и энергии. |
54 |
|
|
жидкость |
94 |
10. Частицы с нулевой массой. |
55 |
17. |
Кипение |
95 |
||
|
|
|
18. |
Уравнение Клапейрона-Клаузиуса |
96 |
|
|
|
|
19.Тройная точка. Диаграмма состояния. 96 |
|||
|
|
|
|
|
Список вопросов к экзамену |
98 |
3
Введение. Векторы
Вектор – это величина, характеризующаяся не только своим численным значением, но и
|
|
r |
|
= |
|
|
|
|
направлением. Модуль вектора – это его длина (число), он всегда >0: |
|
|
2 |
2 |
2 |
|
||
|
|
|||||||
|
a |
|
ax |
+ ay |
+ az . |
|||
Обозначаются векторы стрелкой над буквой - a , в учебниках - жирной буквой. Действия с векторами:
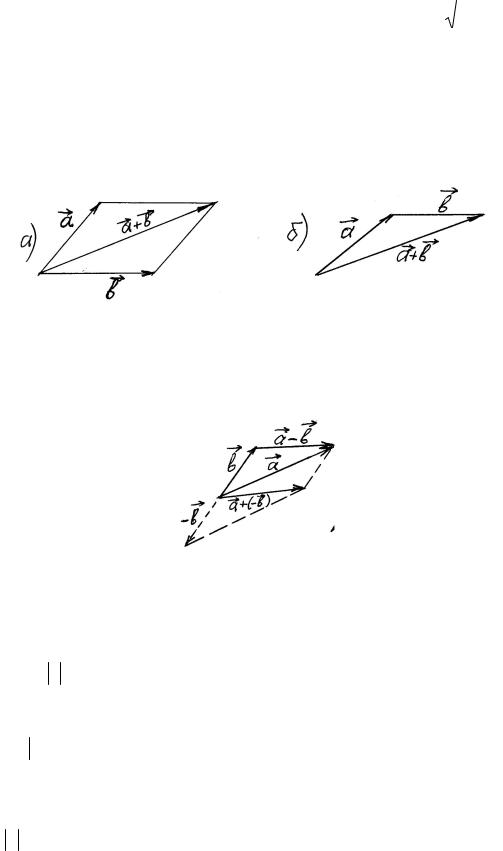
1)Сложение векторов – два способа.
а) по правилу параллелограмма (если исходят из одной точки) б) по правилу треугольника (если следуют один за другим)
2)Вычитание векторов – два способа.
а) Прибавить вектор с противоположным знаком: a − b = a + (−b)
б) Найти вектор, который надо прибавить к b , чтобы получить a.
3) Умножение вектора на число
Вектор ka , где k – число, - это вектор, направленный в сторону a , но с длиной,
большей в k раз. Если k<0, то вектор ka направлен в противоположную a сторону, а его длина больше в k раз.
Единичный вектор (орт) – вектор единичной длины. Обозначается e,i , j,k.
e = a
 a = a / a .
a = a / a .
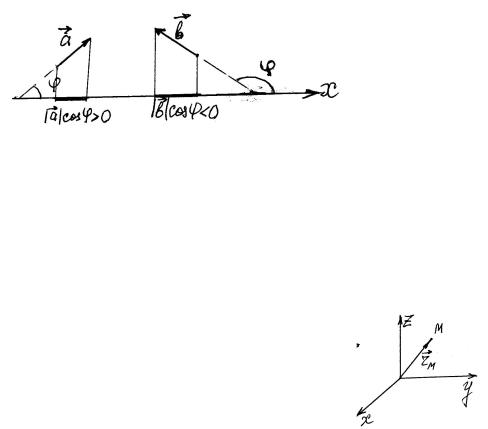
4) Проекция вектора - это число. Она >0, если направление перемещения от проекции начала вектора к проекции его конца совпадает с направлением оси, и <0, если наоборот.
ax = a cosα
Проекция суммы векторов равна сумме проекций: ax = a1x + a2x + a3x .
4
5) Выражение вектора через его проекции на координатные оси
ex = i , ey = j, ez = k
r2 |
= |
|
r |
|
2 |
2 |
2 |
2 |
, если i |
^ j ^ k . |
|
|
|||||||||
a = axi + ay j + azk ; a |
|
a |
|
|
= ax |
+ ay |
+ az |
Квадрат модуля вектора равен сумме квадратов его проекций, только если система
координат декартова, т.е. векторы i , j,k взаимно перпендикулярны.
6) Радиус-вектор точки – это вектор, проведенный в эту точку из начала координат.
rM = xi + yj + zk .
В декартовой системе координат r2 = x2 + y2 + z2 .
Примечание. Правой системой координат называется такая, в которой, если смотреть так, что ось х входит в глаз, то поворот от оси у к оси z происходит против часовой стрелки. Система левая, если наоборот.
7) Скалярное произведение векторов (число).
r |
r |
r |
r |
× |
|
b |
|
× сosα |
a |
× b = ab = (a,b) = |
a |
|
|
||||
|
|
|
|
|
|
|
|
|
Скалярным произведением векторов называется произведение модулей этих векторов и косинуса угла между ними.
r2 |
r |
r |
= |
|
r |
|
× |
|
r |
|
× cos0 = |
|
r |
|
2 |
|
|
|
|
|
|
||||||||||
a |
= a |
× a |
|
a |
|
|
a |
|
|
a |
|
|
|||
i 2 = j 2 = k 2 = 1 ; |
i j = 1×1× cos(π / 2) = jk = i k = 0 |
||||||||||||||
Свойства скалярного произведения.
1)a ×b = ba – переместительный закон.
2)a × (b + c) = ab + ac - распределительный закон.
3) a × b = (axi + ay j + azk )(bxi + by j + bzk ) = axbx + ayby + azbz - через проекции
векторов (!!!)
8) Векторное произведение векторов – это вектор, направленный перпендикулярно плоскости, в которой расположены исходные векторы, причем так, что, если смотреть с его
5
конца, то поворот от первого вектора ко второму происходит против часовой стрелки, а модуль его равен произведению модулей исходных векторов и синуса угла между ними.
a ´ b = [a,b] - обозначение.
r |
´ b |
|
= |
r |
× |
|
b |
|
× sinα |
a |
|
a |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Свойства векторного произведения.
b ´ a = -a ´ b
a ´ (b + c) = a ´ b + a ´ c i ´ i = j ´ j = k ´ k = 0
i × j = k ; j × k = i ; k ´ i = j
a × b = (axi + ay j + azk ) × (bxi + by j + bzk ) = i (aybz − azby ) + j(azbx − axbz ) + k (axby − aybx )
r |
r |
|
i |
j |
k |
|
a |
´ b |
= |
ax |
ay |
az |
- определитель. |
|
|
|
bx |
by |
bz |
|
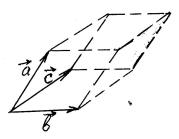
9) Смешанное произведение векторов
a × (b ´ c) = b × (с ´ a) = c × (a ´ b) = ±Vпризмы
Смешанное произведение векторов – это число, модуль которого равен объему призмы,
построенной на основе этих трех векторов. Знак плюс, если векторы a,b,c образуют правую систему координат, минус – если левую.
10) Двойное векторное произведение векторов
a ´ (b ´ c) = b × (a × с) - c × (a ×b) - формула «бац минус цаб».

6
МЕХАНИКА Глава 1. Кинематика.
§1.Скорость.
Материальная точка – тело, размерами которого в данной задаче можно пренебречь. Траектория – линия, по которой движется тело.
Перемещение S - вектор, направленный из начальной в конечную точку траектории.
Путь l – длина траектории (скаляр).
Равномерное прямолинейное движение (РПД) – такое, при котором точка за ЛЮБЫЕ равные промежутки времени совершает одинаковые ПЕРЕМЕЩЕНИЯ.
Скорость РПД – отношение перемещения ко времени, за которое оно произошло.
Средняя скорость (любого движения) - отношение всего перемещения ко времени  v
v = S /t
= S /t
Средняя путевая скорость - отношение полного пути ко времени:  vпутевая
vпутевая  = l / t .
= l / t .
Мгновенная скорость – это предел отношения перемещения ко времени при стремлении промежутка времени к нулю:
vr = lim(DSr/ Dt) = dS |
= Sr&(t) . |
|
t →0 |
dt |
|
Точкой над величиной всегда обозначают производную по времени.
|
vr = dr = rr& |
v = |
|
vr |
|
|
|
Dr |
|
|
|
Dr |
|
|
|
Dr |
||||||
|
|
|
= |
lim |
= lim |
|
|
|
|
¹ lim |
||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
dt |
|
|
|
|
|
|
|
|
t →0 |
Dt |
t →0 |
|
Dt |
|
|
t →0 |
Dt |
||||
|
|
|
|
|
|
|
|
|||||||||||||||
При t → 0 Dl ® |
r |
Þ v = lim |
l |
= |
dl |
& |
|
|
|
|
|
|
|
|
|
|||||||
Dr |
Dt |
dt |
= l |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
t →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
r = xi + yj + zk Þ v = r& = x&i + y&j + z&k , то есть |
vx = x&, |
vy = y&, |
vz = z& |
|||||||||||||||||||
v = |
vx2 + vy2 + vz2 |
= |
x&2 + y&2 + z&2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

7
Можно записать так: v = v ×τ , где τ - единичный вектор касательной к траектории в данной точке, направленный в сторону движения.
n
Найдем путь от t1 до t2 : l = Dl1 + Dl2 + ... + Dln = åDli
i =1
n
li = vi ti , тогда l = åviDti . Устремляя все промежутки времени
i=1
ti |
|
t2 |
|
к нулю, |
получим l = òv(t)dt - для пути. Аналогично для перемещения: |
||
ò2 vr |
(t)dt = ò2 drr |
t1 |
|
= rr12 = Sr |
|||
t |
|
t |
|
t1 |
|
t1 |
|
|
|
|
§2.Ускорение. |
Равноускоренное движение (РУД) – такое, при котором точка за ЛЮБЫЕ равные промежутки времени изменяет свою вектор скорости на одну и ту же величину.
Ускорением РУД называется отношение изменения вектора скорости ко времени, за которое оно произошло.
r |
v2 − v1 |
|
v |
w = |
Dt |
= |
Dt |
При произвольном движении вводятся понятия среднего и мгновенного ускорения:
|
|
|
|
|
|
r |
|
vкон − vнач |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
w |
= |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
= lim |
v |
= |
dv |
r& |
&r& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
Dt |
dt |
= v |
= r - вторая производная по времени от радиус-вектора. |
|||||||||||||||||
|
t →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
w = v&xi + v&y j + v&z k Þ wx = v&x , |
wy = v&y , |
|
|
|
|
|
|
||||||||||||||
|
wz = v&z , w = wx |
+ wy + wz |
|||||||||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
d |
|
r |
r |
r |
r |
|
r |
|
Записав скорость в виде |
v = v ×τ , получим |
w = |
|
|
|
|
(v ×τ ) = v& |
×τ + v |
×τ& |
= w |
+ w , |
||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
τ |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где w = v&×τ - касательное (тангенциальное) ускорение, w = v ×τ& |
- нормальное ускорение, |
||||||||||||||||||||
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
направленное по нормали к траектории. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
wτ = v& |
|
|
|
|
|
|
|
|
|
|
|
|
||
Если v& > 0 , то вектор |
wτ направлен вдоль τ , |
если |
v& < 0, то против, если |
v& = 0 , то |
|||||||||||||||||
w = 0 . |
Нормальное |
ускорение w |
зависит |
от |
τ& , |
|
то есть |
от скорости |
изменения |
||||||||||||
τ |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направления касательной к траектории. Чем траектория сильнее искривлена и чем быстрее

8
движется частица, тем больше wn . Степень искривленности ПЛОСКОЙ кривой
характеризуется кривизной c = lim |
Dϕ . |
l →0 |
Dl |
Пусть точка движется по окружности с
центром О. За время t |
она пришла из А в |
A′ . Тогда Dτ = τ ′ -τ . |
При произвольном |
движении в течение очень малого промежутка времени точка движется по окружности, затем переходит на другую окружность и т.д. Взятие
предела в определении кривизны позволяет считать данный участок дугой окружности (прямая – частный случай окружности с R = ∞ ). Тогда
c = lim |
Dϕ |
= |
1 |
. |
RDϕ |
|
|||
l →0 |
|
R |
||
*****************************************************************************
Напоминание о единицах измерения угла:
1° - центральный угол, опирающийся на дугу, равную 1/360 окружности.
1 радиан - центральный угол, опирающийся на дугу, равную радиусу. Из этого определения следует, что длина дуги окружности равна lдуги = Rϕ , а площадь сектора Sсект = R2ϕ / 2 .
*****************************************************************************
Из полученной формулы ясно, почему величину 1/ с называют радиусом кривизны
|
¢ |
2 |
) |
3 / 2 |
|
кривой в точке. Для ПЛОСКИХ кривых существует формула R = |
(1+ (y ) |
. Радиус |
|||
кр. |
|
y¢¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кривизны – это радиус окружности, сливающейся с данной кривой на бесконечно малом участке. Центр такой окружности называют центром кривизны в данной точке кривой.
Найдем τ& .
r |
|
Dτ |
= lim |
1× Dϕ × n |
|
r |
×ϕ& , где n - нормаль к |
|
|
|||||
τ& = lim |
|
Dt |
|
Dt |
= n |
|
|
|||||||
t |
→0 |
|
|
t →0 |
|
|
|
|
|
|
|
|
||
кривой в точке, n τ . Тогда |
|
|
|
|
|
|
|
|||||||
|
Dl |
|
vDt |
|
|
Dϕ |
|
v |
|
v |
r r v |
|
||
Dϕ = |
|
|
= |
|
Þ |
|
= |
|
Þ ϕ& = |
|
Þ τ& = n |
|
Þ |
|
R |
|
R |
Dt |
R |
R |
R |
||||||||
|
|
|
|
|
|
|
|
|
||||||
r |
r |
v2 r |
|
w |
= v ×τ& = |
|
n |
n |
|
R |
|
|
|
|
|
Итак, полное ускорение равно w = w + w |
|
r |
= |
v2 r |
v& |
2 |
æ v2 |
ö2 |
|
|||
, w = v&×τ , w |
|
n , w = |
|
+ ç |
|
÷ . |
||||||
τ |
n |
τ |
n |
|
R |
|
|
|
ç |
R |
÷ |
|
|
|
|
|
|
|
|
|
è |
ø |
|
||
9
Тангенциальное ускорение wτ ответственно за изменение скорости по модулю, а
нормальное ускорение wn - за ее изменение по направлению.
§3. Равномерное прямолинейное движение.
При равномерном прямолинейном движении вектор скорости остается постоянным,
поэтому для перемещения имеем формулу: S = vt .
Формула сложения скоростей. Абсолютная скорость равна векторной сумме переносной и относительной скоростей: va = vпер + vотн .
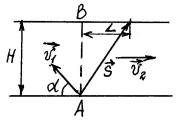
Задача 1. Лодочник, переправляясь через реку шириной h,
все время направляет лодку под углом α к берегу. На какое расстояние течение снесет лодку, если скорость лодки -v1 , а
скорость течения - v2 ?
Решение.
В этом случае переносная скорость – скорость реки, относительная – скорость лодки относительно воды. Тогда абсолютная - скорость лодки относительно берега - равна: v = v1 + v2 . Поскольку оба слагаемых постоянны, то и она постоянна.
Запишем уравнение равномерного прямолинейного движения: S = vt , т.е.
S = (v1 + v2 )t . Проектируя на ось, направленную вдоль течения, и перпендикулярную к ней,
получим систему уравнений:
ìL = (v2 - v1 cosα) ×t1
íîH = v1 sinα ×t1
где t1 - время переправы. Подставляя t1 из второго в первое, получим
L = H (v2 − v1 cosα) . v1 sinα
Задача 2. Две лодки плывут по озеру со скоростями v1 и v2 относительно воды. Чему равна скорость второй лодки относительно первой?
Решение.
Перейдем в систему, связанную с первой лодкой. Тогда переносная скорость – это скорость воды относительно нее, она равна ( −v1 ), относительная – скорость второй лодки относительно воды – равна v2 , абсолютная – скорость второй относительно первой - равна va = vпер + vотн = −v1 + v2 = v2 − v1 . Проверим: при v1 = v2 эта скорость равна нулю, как и должно быть.
|
|
|
|
10 |
|
|
|
|
|
|
|
|
§4. Равноускоренное прямолинейное движение. |
|
|
|
|||||
r |
dv |
выразим |
|
|
|
|
v |
r |
t |
r |
Из w = |
dt |
dv = wdt и, проинтегрировав обе части òdv |
= òwdt , получим |
|||||||
|
|
|
|
|
|
vr0 |
|
0 |
||
|
|
|
S |
r |
t r |
r |
r |
|
wt |
2 |
v = v0 + wt (*). Выражая перемещение òdS = |
òvdt , получим S |
= v0t + |
2 |
(**). |
||||||
|
|
|
0 |
|
0 |
|
|
|
|
|
Проектируя на ось х, совпадающую по направлению с v0 , получим |
|
|
||||||||
|
|
|
v = v0 + wxt |
|
(1) |
|
|
|
|
|
|
|
|
x = v t + |
w t2 |
|
(2) |
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эти формулы дают связи между двумя из трех меняющихся по ходу движения величин
(x,v,t) : первая связывает скорость и время, вторая – модуль перемещения и время. Выведем третью (недостающую) формулу, связывающую скорость и модуль перемещения: dx = v × dt, dt = dv / wx Þ wxdx = v × dv . Интегрируя, получим
S |
v |
|
|
|
òwxdx = òv × dv Þ v2 |
- v02 |
= 2wx S |
(3) |
|
o |
v0 |
|
|
|
При wx > 0 скорость возрастает, при wx < 0 - убывает.
Формулы (1),(2),(3) являются основными для равноускоренного прямолинейного движения, из них можно получить все другие необходимые. Главное их достоинство: каждая из них связывает две из трех переменных. Поэтому поняв, что нужно найти и что дано, можно сразу определить, какая из формул потребуется.
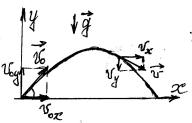
Отметим, что полученные ранее формулы (*) и (**) справедливы не только для прямолинейного движения, но и для криволинейного, но с постоянным вектором ускорения, например, для движения тела, брошенного под углом к горизонту. При решении этой задачи надо обе части этих формул
спроектировать на 2 оси: направленную вверх вертикальную (y), и горизонтальную (x):
ось x: |
vx |
= v0 x ; |
x = v0xt |
|
|
|
ось y: |
v |
y |
= v |
− gt ; y = v |
t - |
gt2 |
|
||||||
|
|
0 y |
0 y |
2 |
||
|
|
|
|
|
||
Легко видеть, что верхние уравнения описывают равномерное движение вдоль оси x, а
нижние – равноускоренное с ускорением (-g) вдоль оси y. Брошенное тело совершает оба эти движения одновременно. К этим формулам можно добавить формулу (3): v02y - vy2 = 2gy .
