
1 курс / Kurs_lektsiy_po_fizike_-_1_semestr1
.pdf71
|
|
( p + |
ν 2a |
)(V −νb) =νRT |
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
V 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p + |
a |
)(V − b) |
|
|
р, атм |
рV, атм*л |
VM2 |
||||||||
|
|
M |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
1 |
1,000 |
|
|
|
1,000 |
|
|||||
|
|
|
|
|
|
|
|
|
|||
100 |
0,994 |
|
|
|
1,000 |
|
|||||
|
|
|
|
|
|
|
|
|
|||
200 |
1,048 |
|
|
|
1,009 |
|
|||||
|
|
|
|
|
|
|
|
|
|||
500 |
1,390 |
|
|
|
1,014 |
|
|||||
|
|
|
|
|
|
|
|
|
|||
1000 |
2,369 |
|
|
|
0,893 |
|
|||||
|
|
|
|
|
|
|
|||||
Из-за взаимного притяжения молекул газ как бы сжимается большим давлением, чем |
|||||||||||
давление на стенках. Отсюда поправка |
|
a |
|
, добавленная к р. Заметное воздействие молекул |
|||||||
VM2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
друг на друга происходит в пределах небольших расстояний, называемых радиусом молекулярного взаимодействия. Сила взаимного притяжения двух элементарных объемов примерно такого радиуса пропорциональна количествам молекул, заключенных в этих объемах. Каждое из них пропорционально числу молекул в единице объема, т.е. обратно пропорционально объему V. Поэтому поправка пропорциональна 1/VM2 . Свободный объем для движения молекул меньше объема сосуда на величину суммарного объема молекул,
поэтому в формуле поправка –b.
Внутренняя энергия В-д-В газа должна включать в себя, кроме кинетической, еще и потенциальную энергию взаимодействия молекул. Силы взаимодействия в уравнении учтены членом a /VM2 . При расширении газа работа, совершенная им против этих сил, равна
dA = |
a |
dV |
. Эта |
работа |
|
идет |
на приращение энергии взаимодействия: |
|||
|
||||||||||
V M2 |
M |
|
|
|
|
|
|
|
|
|
Ep = òdEp = òa /VM2 dVM |
= − |
|
a |
|
+ const . |
Внутренняя энергия газа зависит от |
||||
|
|
|
||||||||
|
|
|
|
|
VM |
|
|
|
||
температуры: |
U = f (T ) − |
a |
. |
При V → ∞ внутренняя энергия должна стремиться к |
||||||
|
||||||||||
|
|
|
|
VM |
|
M |
|
|||
|
|
|
|
|
|
|
||||

72 |
|
|
|
|
C T , т.к. газ можно считать идеальным. В итоге получаем U |
M |
= C T − |
a |
для одного |
|
||||
V |
V |
VM |
|
|
|
|
|
|
моля. Для газа массы m формула принимает вид: Um =νCVT −ν 2a .
V
|
|
|
|
§16.Барометрическая формула. |
|
|
|
|
Рассмотрим газ в поле тяжести. Запишем условие равновесия для |
||
|
|
|
заштрихованного объема, т.е. сила давления снизу должна равняться |
||
|
|
|
сумме силы тяжести и силы давления сверху: |
pS = ( p + dp)S + ρgdhS , |
|
|
|
|
|
|
{ |
|
|
|
|
|
dV |
|
|
|
откуда получаем dp = −ρgdh . |
|
|
Далее будем считать, что температура не зависит от высоты – это частный случай. |
|||||
ρ = m |
= |
Mp |
Þ dp |
= − Mg dh Þ ln p = −Mgh + lnC Þ p = C exp(− Mgh) |
|
V |
|
RT |
p |
RT |
RT |
Пусть p(0) = p0 , тогда окончательно получим p = p0 exp(− MghRT ) .
СТАТИСТИЧЕСКАЯ ФИЗИКА §1.Некоторые сведения из теории вероятностей.
Пусть имеется некоторая макроскопическая система, состоящая из большого числа
частиц. Пусть какая-то характеристика может иметь дискретные значения
Можно сделать N (большое число) измерений х, каждый раз возвращаясь в исходное состояние. Вместо этого можно взять N одинаковых систем в том же состоянии и
одновременно провести |
измерения |
х. |
Такой |
набор систем называется |
статистическим |
|||||||||
ансамблем. Пусть N1 |
|
|
|
|
x1 , |
N2 - |
x2 …, |
NS − xS , причем |
S |
|||||
дали |
значение |
å Ni = N . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
Величина Ni N называется относительной частотой появления результата |
xi |
, а ее предел |
||||||||||||
при N → ∞ называется вероятностью |
|
pi появления результата xi |
|
|
|
|
S |
|||||||
|
. При этом å pi = 1, как |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
и должно быть. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятность получить x |
или |
x |
k |
равна |
p |
= lim |
|
Ni + Nk |
|
= p + p |
k |
- теорема о |
||
|
|
|
||||||||||||
|
i |
|
|
i,k |
N →∞ |
N |
|
i |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
сложении вероятностей. При больших N далее мы будем опускать значок lim.
|
|
|
|
|
73 |
|
|
|
|
|
|
Пусть |
система характеризуется |
значением |
двух |
величин: |
х |
и |
у. Тогда |
||||
p(xi ) = N(xi ) N, p( yk ) = N( yk ) N . |
Найдем вероятность того, что |
при |
некотором |
||||||||
измерении получится xi и yk . Значение |
xi мы получим в |
N(xi ) = p(xi )N |
опытов. |
Из |
|||||||
этого числа |
значение |
yk |
будет |
в |
N (xi , yk ) = p( yk )N(xi ) = p( yk ) p(xi )N , |
т.е. |
|||||
p(xi , yk ) = p(xi ) p(yk ) |
- |
вероятность |
одновременного |
появления |
НЕЗАВИСИМЫХ |
||||||
событий равна произведению вероятностей этих событий. |
|
|
|
|
|
||||||
Найдем среднее значение величины х: |
x = å xi Ni = å pi xi . |
|
|
|
|
||||||
|
|
|
|
|
N |
|
|
|
|
|
|
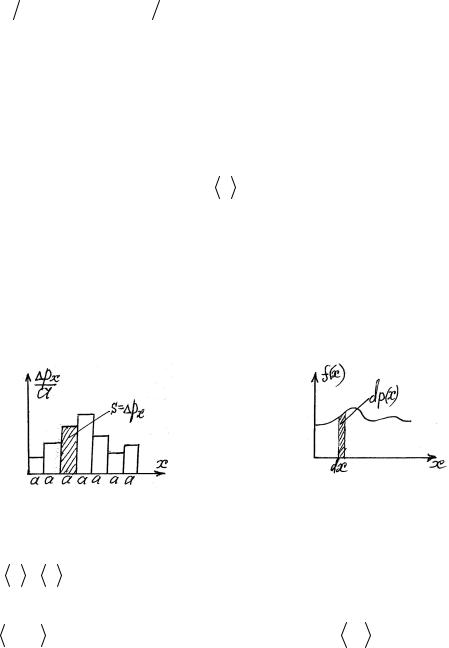
Пусть теперь величина х имеет непрерывный спектр значений от 0 до ∞ . Возьмем |
|||||||||||
очень малую величину a и найдем число измерений |
N0 , |
при котором 0 ≤ x < a , |
N1 , |
||||||||
при котором a ≤ x < 2a и т.д. Тогда вероятность величине х иметь значение от 0 до a равна p0 = N0 / N , от a до 2a - p1 = N1 / N и т.д. Построим гистограмму:
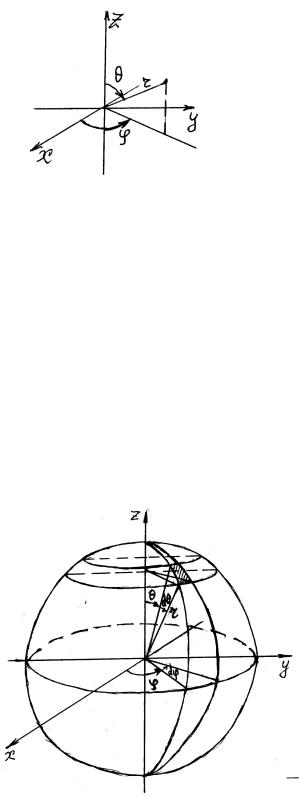
dPx = f (x)dx , |
∞ |
|
|
∞ |
|
|
||
ò |
f (x)dx = |
ò dPx = 1 - площадь под кривой |
f (x). |
|||||
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
∞ |
∞ |
|
|
|
Найдем |
x : |
x |
= |
ò xdPx = ò xf (x)dx . Среднее значение любой функции от х ищется |
||||
|
|
|
|
0 |
0 |
|
|
|
|
|
|
∞ |
|
|
∞ |
|
∞ |
по формуле: |
ϕ(x) |
= òϕ(x)dPx = |
ò |
ϕ(x) f (x)dx. Например, x2 |
= ò x2 f (x)dx . |
|||
|
|
|
0 |
|
|
0 |
|
0 |
Примечание. На вопрос «Сколько молекул в комнате летят со скоростью 100 м/с?» правильным ответом будет: «Ноль!» Дело в том, что спектр скоростей непрерывный. Поэтому ТОЧНОЕ значение 100 м/с не имеет ни одна молекула. Если обнаружится частица со скоростью 100 м/с, то возникнет вопрос про десятые доли, если 100,0, то про сотые и т.д. Правильным вопросом будет такой: «Сколько молекул имеет скорость от 100,00 до 100,01 м/с?». Иначе говоря, надо считать вероятности для скоростей внутри какого-то диапазона, как это и сделано выше.
74
§2. Число ударов молекул о стенку.
Найдем число ударов молекул о площадку площадью
S за время |
t . |
Будем |
вести расчеты в сферических координатах: |
r,θ,ϕ , которые могут изменяться в следующих диапазонах:
0 ≤ r < ∞, 0 ≤ θ < π , 0 ≤ ϕ < 2π . Из аналогии с
-
Телесный угол – область пространства, вырезаемая лучом, проведенным из некоторой точки, после его возвращения в начальное положение (например конус). Измеряется в стерадианах: 1 стерад – телесный угол, вырезающий на сфере радиусом R площадку площадью R2 . Таким образом, любой телесный угол равен отношению площади площадки,
вырезаемой на |
сфере радиуса |
R к |
R2 . |
Полный |
|
|
телесный |
угол |
равен |
|||||||
Sсф / R2 = 4πR2 / R2 = 4π . (Вспомните определение обычного угла и радиана). |
|
|
||||||||||||||
********************************************************************** |
|
|||||||||||||||
Вывод формулы для телесного угла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Найдем площадь области, расположенной |
|||||||||||||
|
|
на |
сфере |
радиуса |
r |
|
между |
двумя близкими |
||||||||
|
|
параллелями: |
θ |
и θ + |
θ и двумя близкими |
|||||||||||
|
|
меридианами: |
ϕ |
|
и |
ϕ + |
ϕ . |
Она |
равна |
|||||||
|
|
произведению сторон «прямоугольничка», т.е. |
||||||||||||||
|
|
DSθ ,ϕ |
= r sinθDϕ × rDθ , |
тогда телесный угол |
||||||||||||
|
|
равен DW |
= DS |
|
/ r2 |
= sinθ × Dθ × Dϕ . |
||||||||||
|
|
|
|
|
|
θ ,ϕ |
|
|
θ ,ϕ |
|
|
|
|
|
|
|
|
|
|
Переходя к бесконечно малым, получим |
|||||||||||||
|
|
|
|
|
|
dWθ ,ϕ |
= sinθ × dθ × dϕ |
|
||||||||
Заодно получим формулу для элемента объема |
dV |
|
в сферических координатах, т.е. |
|||||||||||||
объема области r0 |
≤ r < r0 + dr, θ0 |
≤ θ < θ0 + dθ , |
ϕ0 |
≤ ϕ < ϕ0 + dϕ : |
|
|
|
|||||||||
|
dV = dS × dr = r2 ×sinθ |
0 |
× dθ × dϕ × dr |
|
|
|
|
|
|
|||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

75
************************************************************************
|
|
Из общего числа молекул N скорость от v до v+dv имеют |
|||||||||||||
dNv |
штук. |
Из |
них |
в |
телесном |
угле |
dΩ |
летит |
|||||||
dN |
v,θ ,ϕ |
= dN |
v |
dΩθ ,ϕ |
. За |
время |
t |
до |
стенки |
долетают все |
|||||
4π |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
молекулы, заключенные в косом цилиндре с основанием |
S и |
||||||||||||||
высотой v |
t cosθ . |
Их |
доля равна |
отношению |
объема |
этого |
|||||||||
цилиндра ко всему объему V, т.е. их количество равно |
|
|
|
|
|
||||||||||
|
dΩθ ,ϕ |
|
Sv |
|
t cosθ |
|
sinθ |
Sv |
t cosθ θ |
ϕ |
|
||||
dKv,θ ,ϕ = dNv |
|
|
|
|
V |
= dNv 4π |
|
V |
|
|
|||||
4π |
|
|
|
|
|
|
|||||||||
Количество ударов о площадку |
|
S за время |
t молекул, |
летящих со скоростью от v |
|||||||||||
до v+dv со всех возможных направлений, получим, проинтегрировав (просуммировав) все dKv,θ ,ϕ по ϕ от 0 до 2π и по θ от 0 до π / 2 (а не до π , так как часть молекул летит от стенки, а не к ней).
dKv |
= dNv |
v S |
t π / 2 |
2π |
|
|
|
|
|
|
|
|
4πV |
òsinθ cosθ dθ ò dϕ |
|
|
|
|
|
|
|
|
|||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
π / 2 |
sinθ cosθ dθ = |
π / 2 |
|
2 |
θ |
|
π / 2 |
= |
1 |
|
||
|
|
|
||||||||||
|
|
|
|
|||||||||
Вычислим интеграл: ò |
òsinθ d(sinθ ) = sin |
|
|
|
, тогда |
|||||||
0 |
|
|
|
0 |
2 |
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dK |
v |
= dN |
v |
v S t |
- количество молекул со скоростью от v до v+dv, ударяющихся о |
|||||||||||||
|
|
|
|
4V |
|
|
|
|
|
|
|
|
|
|
|
|
||
площадку |
|
S за время |
t . |
|
|
|
|
|
|
|
|
|
|
|
||||
Чтобы узнать общее количество ударов о площадку молекул с любыми скоростями, |
||||||||||||||||||
надо проинтегрировать по всем скоростям: |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
t) = |
S t ∞ |
= |
S t |
∞ |
dN |
v |
= |
S t |
N v = |
S t |
|
|
|
|
K( S, |
|
òvdNv |
|
N òv |
|
|
|
n v , |
||||||||
|
|
4V |
4V |
N |
|
4V |
4 |
|||||||||||
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
123 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
v =ò vdp |
|
|
|
|
|||
где n = |
N |
- концентрация молекул. Считая |
S =1 м2, |
t =1 с, найдем количество ударов |
||||||||||||||
V |
|
|||||||||||||||||
за единицу времени (1 секунду) о площадку единичной площади (1 м2): K = 14 n v
v

76
§3. Основное уравнение МКТ.
Рассмотрим абсолютно упругий удар одной молекулы о стенку
( v2 = v1 = v ). Импульс, отданный молекулой стенке, равен
DP = mv1 - mv2 = 2mvcosθ × n .
Все dKv,θ ,ϕ ударов отдадут стенке импульс
dPv,θ ,ϕ = dKv,θ ,ϕ 2mvcosθ . Импульс, имеющий модуль dP , направлен вдоль n , т.е. давит
на стенку. Просуммируем по углам:
|
dPv = dNv mv |
2 |
|
|
π / 2 |
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
mv |
2 |
|
|||||
|
|
DSDt òcos2θ sinθ dθ |
ò dϕ =dNv |
DSDt |
|
|||||||||||||||||||||||
|
|
2πV |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
3V |
|
|
||||
|
|
|
|
|
|
|
1442443123 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
cos3 |
θ |
|
|
π / 2 |
= |
1 |
|
2π |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
0 |
3 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v2 dNv |
= m × DS × Dt × N |
|
||||
Проинтегрируем по скоростям: |
DP = m × DS × Dt × N ò |
|
v2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vmax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
3V |
|
|
|
|
|
|
|
|
|
|
|
3V |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
Найдем давление: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p = |
F |
= |
|
|
P |
|
|
|
= |
1 mn v2 |
= |
2 n εпост , |
|
|
||||||||||||
|
|
DS |
Dt × DS |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|||||||||||
при выводе |
мы учли, |
что |
|
F = |
|
P |
. |
|
|
|
Здесь |
|
εпост |
|
- средняя |
кинетическая |
энергия |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
Dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
поступательного движения молекулы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Мы |
получили |
основное |
уравнение |
|
|
МКТ |
|
p = 1 mn v2 , связывающее |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||
макроскопическую величину р с микроскопическими m, n и v молекул. |
|
|||||||||||||||||||||||||||
|
|
|
|
§4. Средняя энергия молекул. |
|
|
|
|||||||||||||||||||||
Из уравнения Менделеева-Клапейрона pV =νRT = |
|
N |
RT следует: |
|
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NA |
|
|
|
|
|
|
|
|
|
|
|
p = |
N |
|
RT |
= nkT , |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
NA |
V |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где k = R / NA = 1,38×10−23 Дж/К – постоянная Больцмана, n – концентрация. |
|
|||||||||||||||||||||||||||
Из соотношений p = 2 n εпост и p = nkT следует, что εпост |
= 3 kT . |
|
||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Эта формула позволяет понять, что же такое температура. Абсолютная температура – это величина, прямо пропорциональная средней энергии молекул. В принципе, коэффициент

77
можно было бы положить равным 1, тогда температура измерялась бы в Джоулях. Но исторически сложилось так, что температуру измеряют в Кельвинах, так что постоянная Больцмана k – это всего лишь коэффициент для пересчета Кельвинов в Джоули.
Введем понятие числа степеней свободы. Числом степеней свободы механической системы называется минимальное количество независимых величин, с помощью которых может быть задано положение системы. Например, точка – 3 координаты, абсолютно твердое тело – 6 (3 поступательных – координаты какой-то точки, например центра масс, и 3 вращательных – углы поворота вокруг трех осей).
Система из N точек имеет 3N степеней свободы. Любая жесткая связь уменьшает их число на единицу. Например, молекула из двух атомов имеет 6-1=5 степеней свободы, т.к. расстояние между атомами остается постоянным. Из этих пяти степеней свободы 3 поступательных и 2 вращательных, т.к. вокруг продольной оси молекулы вращения нет. Если связь не жесткая, а упругая, то степеней свободы будет 6, добавится 1 колебательная. Если все N точек связаны упругими связями, то из 3N степеней свободы будут 3 поступательных,
3 вращательных и остальные 3N-6 – колебательные. Для линейной молекулы число вращательных на одну меньше, значит, колебательных на одну больше.
В классической (не квантовой) статистической физике доказывается закон равнораспределения (Больцман), согласно которому на каждую степень свободы молекулы приходится энергия kT / 2, т.е.  ε
ε  = ikT / 2 , где i = nпост + nвращ + 2nкол . Коэффициент 2
= ikT / 2 , где i = nпост + nвращ + 2nкол . Коэффициент 2
соответствует тому, что колебательное движение имеет кинетическую и поступательную составляющие и на каждую приходится по kT/2.
Для идеального газа, в котором отсутствует взаимодействие молекул, внутренняя
энергия моля равна UM = NA ε |
|
= iRT |
. Тогда |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
C = |
i |
R , |
|
C |
p |
= C + R = |
i + 2 |
R , |
γ = |
Cp |
= |
i + 2 |
|||
|
|
|
|
|
|
||||||||||
V |
2 |
|
|
|
|
V |
|
2 |
|
|
|
CV |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Однако все не совсем так. Причина тому – квантовая |
|
|
|
|
|||||||||||
механика. |
|
|
Для |
трехатомной |
|
молекулы |
|
|
|
|
|||||
i = 3пост + 3вращ + 2(3×3 - 6)колеб |
= 12 , |
для |
4-атомной |
|
|
|
|
||||||||
i=3+3+2(12-6)=18, для 2-атомной i=3+2+2(6-5)=7. А |
|
|
|
|
|||||||||||
на опыте теплоемкости соответствуют значениям i=6, 6 и |
|
|
|
|
|||||||||||
5. Мало |
того, |
с ростом |
температуры С |
меняется, |
|
|
|
|
|||||||
соответствуя увеличивающимся значениям i.

78
Причина в том, что при малых T задействованы только поступательные степени свободы, с ростом Т подключаются вращательные, и только при больших Т начинают проявляться колебательные. При этом, как следует из характера графика, во вращение, а потом и в колебания вовлекаются не сразу все молекулы, сначала небольшая их доля, потом больше и больше, пока не вовлекутся все. Объяснение состоит в том, что вращательная и колебательная энергии квантуются, т.е. энергия может меняться только скачками. Поступательная скачков не имеет.
Величина кванта колебательной энергии на порядок выше, чем вращательной. При низких 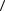 ε
ε  ,
,
т.е. Т, очень мало молекул может иметь энергию порядка Евращ,1 . Далее с ростом 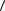 ε
ε  вовлекается
вовлекается
вращательное движение, а потом и колебательное. У разных многоатомных молекул характерные значения энергий различны, поэтому при одной и той же Т у одних веществ какие-то степени свободы
уже задействованы, а у других – нет. У большинства при комнатных температурах задействованы поступательные и вращательные, а колебательные подключаются при высоких температурах.
§5. Распределение Максвелла.
Мы знаем, что молекулы газа находятся в непрерывном движении. Но с какими скоростями они движутся? Как они распределены по скоростям? Ответы на эти вопросы дает распределение Максвелла, выведенное теоретически в 1860 году. Эта теория является ярким примером научной изобретательности и мощи человеческого разума. На первый взгляд, не за что даже зацепиться, чтобы получить ответы на интересующие нас вопросы. И, тем не менее, Джеймс Кларк Максвелл построил свою теорию, пользуясь только карандашом и бумагой. Никаких дополнительных экспериментов!
Рассмотрим так называемое пространство скоростей. Скорости каждой молекулы соответствует точка в этом пространстве. Из-за столкновений эти точки движутся, но их плотность (концентрация) в каждом месте остается постоянной (газ в равновесии). Из-за равноправия всех направлений движения расположение точек будет
сферически симметрично, т.е. плотность (концентрация) точек в пространстве скоростей зависит только от модуля скорости v = v . Обозначим эту концентрацию через N × f (v) ,
где N – полное количество молекул. Тогда количество молекул с проекциями скорости

|
|
|
|
|
|
|
|
|
|
|
79 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
между vx |
и ( vx + dvx ), |
vy и (vy |
+ dvy ), vz |
и ( vz |
+ dvz ) |
можно записать в виде (все |
|||||||||||||||||||||||||||
молекулы в кубике): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dNvx ,v y ,vz |
= Nf (v)dvxdvy dvz |
|
|
|
|
|||||||||||||||
|
|
|
|
|
Молекулы |
со скоростями |
от |
v |
до v + dv |
находятся |
внутри |
||||||||||||||||||||||
|
|
|
|
|
шарового |
|
слоя. |
|
|
Количество |
их |
|
равно |
|
|
dNv |
= Nf (v)4πv2dv |
||||||||||||||||
|
|
|
|
|
(площадь поверхности сферы на толщину слоя). Вероятность |
||||||||||||||||||||||||||||
|
|
|
|
|
молекуле иметь такую скорость равна dp |
= |
|
dNv |
|
= f (v)4πv2dv . |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
N |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вид функции |
f (v) |
и установил Максвелл в 1860 году. Вероятности молекуле иметь |
|||||||||||||||||||||||||||||||
проекции скорости между vx и ( vx + dvx ), |
vy и ( vy + dvy ), vz |
и ( vz |
+ dvz ) равны: |
|
|
|
|||||||||||||||||||||||||||
|
|
dpvx = ϕ(vx )dvx ; |
|
dpv y |
|
= ϕ(vy )dvy ; |
dpvz |
|
= ϕ(vz )dvz |
|
|
|
|
||||||||||||||||||||
Из-за равноправности направлений |
|
|
движения |
|
вид ϕ |
|
один |
|
и |
тот же. Максвелл |
|||||||||||||||||||||||
предположил, что вероятности dpvx |
, dpvy |
, |
|
dpvz |
являются независимыми. Тогда |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
dpvx ,v y ,vz |
= ϕ(vx )ϕ(vy )ϕ(vz )dvxdvy dvz , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
как произведение вероятностей независимых событий, а |
f (v) = ϕ(vx )ϕ(vy )ϕ(vz ) . |
|
|
|
|||||||||||||||||||||||||||||
Возьмем логарифм от обеих частей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
ln f (v) = lnϕ(vx ) + lnϕ(vy ) + lnϕ(vz ) |
|
|
|
|
|
|
|
|
(*) |
|
|
|
||||||||||||||||||
Продифференцируем обе части по vx : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
f '(v) |
|
∂v |
ϕ'(vx ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
= ϕ(vx ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
f (v) |
|
|
¶vx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
∂v |
|
|
|
|
|
2vx |
|
|
= vx . |
|||||||||||||||
Из формулы v = |
vx2 + vy2 + vz2 |
найдем частную производную: |
= |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶vx |
|
|
2 vx2 |
+ vy2 + vz2 |
|
|
v |
||||
Тогда |
|
f '(v) |
× vx |
= ϕ'(vx ) |
|
Þ |
|
|
|
|
f '(v) |
= |
ϕ'(vx ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
ϕ(vx )vx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
f (v) v |
ϕ(vx ) |
|
|
|
|
|
|
f (v)v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Правая часть не зависит от vy |
|
и vz , |
значит, и она, и левая часть являются функциями |
||||||||||||||||||||||||||||||
только от vx . Аналогично, беря производные по vy и vz , докажем, |
что левая часть является |
||||||||||||||||||||||||||||||||
функцией только от vy и vz . Иначе говоря, она не зависит ни от vx , |
ни от vy , ни от vz , т.е. |
||||||||||||||||||||||||||||||||
является константой (−α) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
80
|
ϕ'(vx ) |
= -α Þ ϕ'(vx ) = -αvx |
Þ d lnϕ(vx ) = -αvx Þ lnϕ(vx ) = |
-αvx2 |
+ ln A |
|||||||
|
|
|||||||||||
ϕ(vx )vx |
ϕ(vx ) |
|
|
|
|
dvx |
|
2 |
|
|||
Окончательно: ϕ(vx ) = A × exp(-αvx2 ) . Аналогично можно показать, что |
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-αvy2 |
-αv2 |
|
|
||
|
|
ϕ(vy ) = |
A × exp( |
|
|
) и ϕ(vz ) = A × exp( |
z ). |
|
|
|||
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
-αv |
2 |
|
|
|
|
|
|
|
||
Тогда f (v) = A |
× exp( |
|
|
). |
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|||||
Постоянную А найдем из условия нормировки: |
|
|
|
|||||||||
|
∞ |
∞ |
|
2 |
|
|
|
|
|
|
||
|
òdpvx =1 Þ A ò×exp(-αvx )dvx |
= 1 |
|
|
|
|||||||
−∞ |
−∞ |
2 |
|
|
|
|
|
|
|
|
||
Для взятия интеграла воспользуемся формулой для интеграла Эйлера-Пуассона:
|
|
|
|
∞ |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|||
|
|
|
|
òexp(-βx2 )dx = |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-αvx2 ) |
|
|||||
и получим: A × |
2π |
|
= 1, т.е. |
A = |
|
α |
и ϕ(vx ) = |
|
|
α |
|
|
× exp( |
|
|||||||||
α |
|
2π |
|
|
|
2π |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
Запишем выражение для средней энергии: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ε = |
m(vx2 + vy2 + vz2 ) |
|
|
m |
2 |
|
2 |
|
2 |
|
|
3m |
2 |
||||||||||
|
|
|
|
|
= |
|
( vx |
+ |
vy |
+ vz |
) = |
|
vx . |
||||||||||
2 |
|
|
|
2 |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Приравнивая эту величину к 3kT / 2 , получим: |
|
vx2 = kT |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
Чтобы найти α , вычислим  vx2
vx2 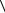 и приравняем к значению kT/m.
и приравняем к значению kT/m.
Чтобы найти  vx2
vx2 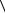 , возьмем производную от интеграла Пуассона по β :
, возьмем производную от интеграла Пуассона по β :
|
òexp(-βx2 )dx = |
π |
|
|
Þ - ò x2 |
exp(-βx2 )dx = |
|
|
|
π (- 1)β −3 / 2 |
|
|
|
|
|
|
|
|
|||||||||||
|
∞ |
|
|
|
|
β |
∞ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
−∞ |
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|||||
Воспользуемся формулой другого интеграла Эйлера-Пуассона |
ò x2 exp(-βx2 )dx |
= |
|
|
: |
||||||||||||||||||||||||
|
2β 3 / 2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|||||||
|
∞ |
|
|
|
|
|
∞ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
2 |
2 |
|
|
|
α |
|
2 |
|
|
α |
|
π |
|
|
|
|
|
|
|||||||||||
vx |
= ò |
vx |
ϕ(vx )dvx |
= |
|
|
|
|
òvx |
exp(-αvx |
/ 2)dvx = |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
2(α / 2)3 / 2 |
α |
|
|
|
|
|
||||||||||||||||
|
−∞ |
|
14243 |
|
|
2π −∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
dpvx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приравнивая  vx2
vx2  = kTm , получим α = m/ kT . Окончательно:
= kTm , получим α = m/ kT . Окончательно:
