Алгебраические основы информатики
.docxФедеральное государственное бюджетное образовательное учреждение
высшего образования
«Саратовский государственный технический университет
имени Гагарина Ю.А.»
Институт прикладных информационных технологий и коммуникаций
Кафедра «Информационно-коммуникационные системы и программная инженерия»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Алгебраические основы информатики»
Вариант №2
Саратов 2023
Вариант № 2
Для
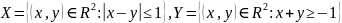 построить
построить
 .
.
Решение:


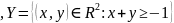
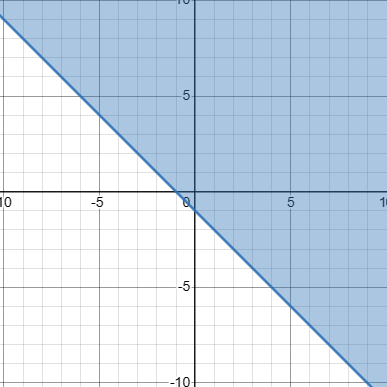

Область пересечения включает в себя часть прямой из X и Y.
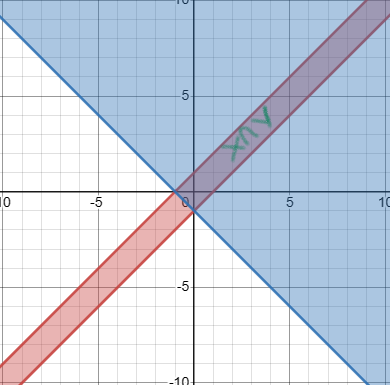

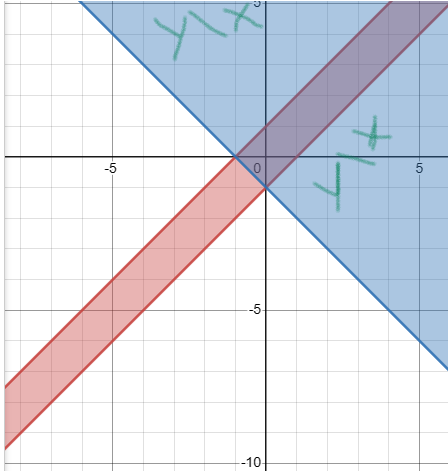
Область, которая имеет голубой цвет. Прямая из Х не входит в эту область.
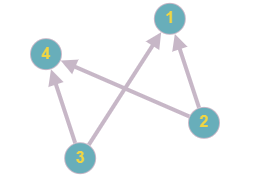
Изобразить графы и найти матрицы отношений
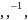 для бинарных отношений на множестве A
{1,2,3,4}
: {(2,1),(1,2),(3,3),(2,4)},
{(1,2),(1,3),(4,2),(4,3)}.
для бинарных отношений на множестве A
{1,2,3,4}
: {(2,1),(1,2),(3,3),(2,4)},
{(1,2),(1,3),(4,2),(4,3)}.
Решение:



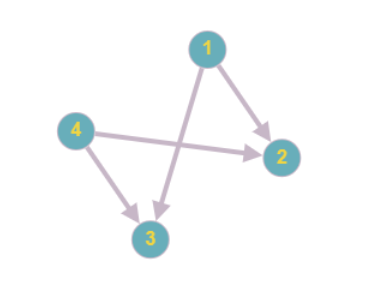



Какими свойствами обладает бинарное отношение на множестве R, если
 .
.
Решение:
Рефлексивность:
 не
выполняется при
не
выполняется при
 ,но выполняется для всех других x.
Следовательно, данное отношение
нерефлексивно.
,но выполняется для всех других x.
Следовательно, данное отношение
нерефлексивно.
Симметричность: из
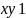 следует
следует
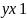 на
основании переместительного свойства
умножения. Пример:
на
основании переместительного свойства
умножения. Пример:


 -
верно. Следовательно, данное отношение
симметрично.
-
верно. Следовательно, данное отношение
симметрично.
Транзитивность: из и
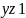 не
всегда следует
не
всегда следует
 . Пример:
. Пример:
 Следовательно,
данное отношение не транзитивно.
Следовательно,
данное отношение не транзитивно.
Вывод: данное отношение на указанном множестве обладает свойством симметричности, а свойствами рефлексивности и транзитивности - нет.
На множестве R задано бинарное отношение
 Доказать, что
– эквивалентность и описать ее классы
эквивалентности.
Доказать, что
– эквивалентность и описать ее классы
эквивалентности.
Решение:
Отношение эквивалентности — всякое рефлексивное, транзитивное и симметричное отношение;
а) рефлексивным, свойство R рефлексивно если для любого x из множества, для которого определено отношение справедливо (a, a) є R
 выполняется
условие рефлексивной.
выполняется
условие рефлексивной.
б) симметричным, если для любого a, b из множества, для которого определено отношение справедливо (a, b) є R => (b, a) є R
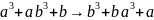
Выполняется условие симметричности.
с) транзитивным, если для любого a, b, c из множества, для которого определено отношение справедливо (a, b) є R & (b, c) є R => (a, c) є R

Следует
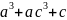
1.

2.

3.
Подсчитали
то, что
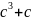 равно
равно
 ,и
получили выражение 1
,и
получили выражение 1
Свойство транзитивности выполняется.
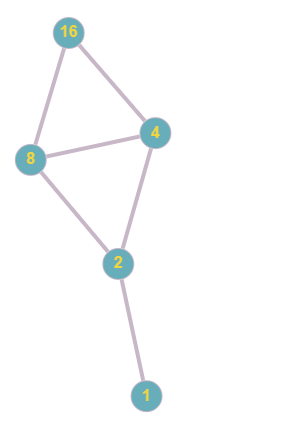
Пусть D (16) – множество всех натуральных делителей числа 16, упорядоченное отношением делимости. Построить диаграмму Хассе этого упорядоченного множества и описать специальные элементы.
Решение:
Составим множество.
{1, 2, 4, 8, 16}