
[2сем]_Мат_ответы_v2
.pdf
1. Линия на плоскости ХОУ, в точках которой функция z=f(x,y) сохраняет постоянное значение
называется линией ...
уровня
2. Производная неявно заданной функции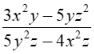 равна:
равна:
|
|
|
|
|
|
|
|
|
|
|
|
3. Производная |
неявно заданной функции |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Производная |
неявно заданной функции |
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
5. Производная |
неявно заданной функции |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
6. Производная |
неявно заданной функции |
|
|
|
|
|
|
|
7.Производная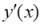 неявно заданной функции
неявно заданной функции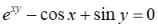
8.Производная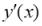 неявно заданной функции
неявно заданной функции 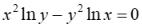
9.Для дифференциального уравнения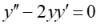 , допускающего понижение порядка, результат понижения порядка на одну единицу равен:
, допускающего понижение порядка, результат понижения порядка на одну единицу равен:

10. |
Общее решение линейного однородного дифференциального уравнения |
: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
Частная производная |
функции |
|
равна: |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
12. |
Частная производная |
функции |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
13. |
Частная производная |
функции |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
14. |
Частная производная |
функции |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
15. |
Частная производная |
функции |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.Полный дифференциал второго порядка функции z=f(x,y) имеет вид
17.Частное решение линейного неоднородного уравнения
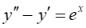 :
:
18. Частное решение линейного неоднородного уравнения

19. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в …
тождество
20. Уравнение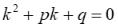 называется … уравнением для дифференциального уравнения
называется … уравнением для дифференциального уравнения
характеристическим
11. Наивысший порядок производной, входящей в дифференциальное уравнение, называется … этого уравнения
порядок
21. Если дифференцируемая функция z=f(x,y) в точке Р(х1,у1) имеет экстремум, то частные производные первого порядка равны:
0
22. Совокупность любых двух линейно независимых на интервале (a,b) частных решений линейного однородного дифференциального уравнения второго порядка называется … системой решений этого уравнения
фундаментальной
23. Дифференциальное уравнение называется однородным, если функция
называется однородным, если функция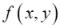 является однородной функцией … порядка
является однородной функцией … порядка
нулевого
24.Частным приращением функции z=f(x,y) по переменной у называется выражение
25.Среди стационарных точек функции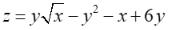 имеется точка
имеется точка
А(4,4)
26. Среди стационарных точек функции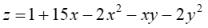
Р(4,-1)
27. Среди стационарных точек функции М(1,0.5)
М(1,0.5)
28. Среди стационарных точек функции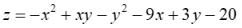 имеется точка
имеется точка
M(-5; -1)

29. Среди стационарных точек функции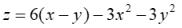 имеется точка
имеется точка
М(1,-1)
30. Для дифференциального уравнения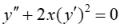 допускающего понижение порядка, результат понижения порядка на одну единицу равен
допускающего понижение порядка, результат понижения порядка на одну единицу равен
31.Для дифференциального уравнения 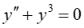 опускающего понижение порядка, результат понижения порядка на одну единицу равен
опускающего понижение порядка, результат понижения порядка на одну единицу равен
32.Общее решение линейного однородного дифференциального уравнения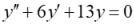
33.Общее решение линейного однородного дифференциального уравнения
34.Общее решение линейного однородного дифференциального уравнения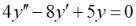
35.Общее решение линейного однородного дифференциального уравнения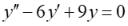
36.Частное решение линейного неоднородного уравнения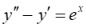
равно
37.Частное решение линейного неоднородного уравнения 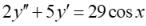
38.Частное решение линейного неоднородного уравнения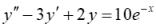

39. |
Выражение |
называется определителем … для двух дифференцируемых функций |
|
|
|
и |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вронского |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
40. |
Радиус сходимости степенного ряда |
равен 6. Тогда интервал сходимости имеет вид … |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(-6; 6) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||||
41. |
Радиус сходимости степенного ряда |
равен 5. Тогда интервал сходимости имеет |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(-6; 4) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||||||||
42. Укажите правильное утверждение относительно сходимости числовых рядов А) |
и В) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
А - сходится, В – расходится |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44. |
Если |
то числовой ряд |
сходится при |
|
||
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
||
45. |
Радиус сходимости степенного ряда |
равен 2. Тогда интервал сходимости имеет вид … |
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(-2; 2) |
|
|
|
|

46. Радиус сходимости степенного ряда |
равен 5. Тогда интервал сходимости имеет вид |
|||
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(-6; 4)
47. Укажите правильное утверждение относительно сходимости числовых рядов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А и В сходятся |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
48. Если |
|
, то числовой ряд |
сходится при , равном … |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
49. Коэффициент |
разложения функции |
в ряд Фурье на отрезке |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
50. Коэффициент |
разложения функции |
в ряд Фурье на отрезке |
: |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
