Tema_5_Statisticheskie_pokazateli

Статистические

показатели

ТЕМА 5

Показатели, используемые в экономикостатистическом анализе:

должны иметь реальный смысл

характеризовать определенные категории и понятия

рассчитываться или учитываться на основе теоретического анализа явления

В каждой конкретной области приложения

статистики разрабатывается своя система

показателей

12.09.2016

В зависимости от того, какая сторона или особенность социально-экономического явления изучается, в теории статистики выделяются различные статистические показатели:

Абсолютные, относительные и средние величины

Показатели вариации

Показатели рядов динамики

Системы индексов

Показатели тесноты связи и характеристики функциональных зависимостей

Экономико-статистические показатели отдельных сфер деятельности

Статистические

показатели могут представлять собой абсолютные, относительные или средние величины

ЛЕКЦИЯ 9

Абсолютные и относительные величины и их характеристика

ПОНЯТИЕ АБСОЛЮТНОЙ ВЕЛИЧИНЫ И ЕЕ ХАРАКТЕРИСТИКА

Результаты статистического наблюдения

регистрируются как абсолютные величины

Абсолютные величины являются исходной формой выражения статистических показателей

Абсолютная величина - показатель размеров общественных явлений в конкретных условиях места и времени

Например, внутренний валовой продукт (ВВП), национальный доход (НД), объем промышленного производства, численность населения РФ

ВИДЫ АБСОЛЮТНЫХ ВЕЛИЧИЯ

УСЛОВНО-НАТУРАЛЬНЫЕ ЕДИНИЦЫ ИЗМЕРЕНИЯ

Применяются для соизмерения разнородных, но взаимозаменяемых по какому-либо свойству объектов:

разные виды топлива соизмеряются по условному топливу с установленной теплотворной способностью единицы веса 7000 ккал/кг

консервы – по условным консервным банкам объемом 353,4 куб.см

Перевод в условные единицы осуществляется на основе специальных коэффициентов:

К= Потребительское свойство / Эталон

12.09.2016

ВИДЫ АБСОЛЮТНЫХ ВЕЛИЧИЯ

•характеризуют размеры признака отдельных единиц

совокупности (численность Индивидуальные работающих на конкретном

величины предприятии)

АБСОЛЮТНЫЕ ВЕЛИЧИНЫ – ЭТО ИМЕНОВАННЫЕ ЧИСЛА, т.е. ИМЕЮЩИЕ КАКУЮ-ЛИБО ЕДИНИЦУ ИЗМЕРЕНИЯ

ПОНЯТИЕ ОТНОСИТЕЛЬНОЙ ВЕЛИЧИНЫ И ЕЕ ХАРАКТЕРИСТИКА

Абсолютные величины не всегда полно характеризуют явления

Чтобы правильно оценить тот или иной абсолютный показатель, необходимо сравнить его с планом, фактом или показателем, принадлежащим к другому периоду. Для этого применяются относительные величины

12.09.2016

Сравниваемая величина – плановая, текущая или отчетная величина

Основание, базисная величина или база сравнения - величина, с которой сравнивают

Сравниваемая текущая, плановая или отчетная величина

Основание, база сравнения, базисная величина

ДЛЯ ВЫРАЖЕНИЯ РЕЗУЛЬТАТА СОПОСТАВЛЕНИЯ ОДНОИМЕННЫХ ВЕЛИЧИН

•применяется в статистике

населения: показатели рождаемости, смертности, заключенных браков

•в расчет на десять тысяч

определяется число продецимилле студентов вузов,

численность врачей и т.д.

ВИДЫ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН ПО СОДЕРЖАНИЮ

во времени

Относительные

величины

характеризуют

соотношения

показателей

по составу и внутренним в пространстве

связям

РАСЧЕТ ЦЕПНЫМ И БАЗИСНЫМ СПОСОБОМ

Если уровень каждого последующего периода

(Уn) сопоставляют с уровнем предшествующего периода (Уn-1), то ОВД рассчитывается

цепным способом.

ОВДцепная = Yn /Yn-1 *100%

Если уровень каждого последующего периода

(Уn) сопоставляют с уровнем, принятым за базу сравнения (У0), то ОВД рассчитывается

базисным способом:

ОВДбазисная = Yn / Y0 *100%

ДЛЯ ХАРАКТЕРИСТИКИ ЯВЛЕНИЯ ВО ВРЕМЕНИ

ОВВП - относительная величина выполнения плана

Характеризует рост или сокращение исследуемого явления, фактически достигнутого в отчетном периоде, по сравнению с планом

Результат сравнения фактически достигнутого уровня показателя с его плановым уровнем

ОВВП = Y 1 / Y пл * 100%,

где Y1 - уровень показателя, достигнутый в отчетном периоде

12.09.2016

ДЛЯ ХАРАКТЕРИСТИКИ ЯВЛЕНИЯ ВО ВРЕМЕНИ

 ОВД - относительная величина динамики

Характеризует изменение уровня развития тех или иных явлений во времени

Рассчитывается как отношение текущего показателя к предшествующему или базисному:

ОВД = Y 1 / Y 0 * 100%,

где Y1 – уровень показателя в предшествующем периоде

Yо - уровень показателя в прошлом (предыдущем, базовом) периоде

ДЛЯ ХАРАКТЕРИСТИКИ ЯВЛЕНИЯ ВО ВРЕМЕНИ

ОВПЗ - относительная величина планового задания

Характеризует рост или сокращение исследуемого явления в плановом периоде по сравнению с уровнем, достигнутым в предшествующий период

Рассчитывается как отношение величины показателя, устанавливаемого на плановый период, к его фактической величине, достигнутой за предшествующий период или за какой-либо другой, принятый за базу сравнения

ОВД = Y пл / Y 0 * 100%,

где Yпл - уровень, запланированный на предстоящий период

Yо - уровень показателя в прошлом (предыдущем, базовом) периоде

РАЗНОВИДНОСТИ ОТНОСИТЕЛЬНЫХ ПОКАЗАТЕЛЕЙ ВЫПОЛНЕНИЯ ПЛАНА

Сравнение плановых и фактических уровней

Сравнение абсолютных величин

прироста или снижения показателя по плану и факту

Пример. Планировалось снизить себестоимость единицы продукции на 24,2 руб., а фактическое снижение составило 27,5 руб., тогда уровень

выполнения планового задания по снижению себестоимости: 27,5 / 24,2 =

1,136, т.е. план по снижению уровня себестоимости перевыполнен на 13,6%

МЕЖДУ ОТНОСИТЕЛЬНЫМИ ВЕЛИЧИНАМИ ПЛАНОВОГО ЗАДАНИЯ, ВЫПОЛНЕНИЯ ПЛАНА И ДИНАМИКИ СУЩЕСТВУЕТ СЛЕДУЮЩАЯ ВЗАИМОСВЯЗЬ:

ОВД = ОВВП * ОВПЗ

Пример. Предположим, что оборот торговой фирмы в 2014 г. составил 2,0 млрд. руб. Исходя из проведенного анализа складывающихся на рынке тенденций руководство фирмы посчитало реальным в следующем году довести товарооборот до 2,8 млрд. руб. Фактически оборот фирмы в 2014 году составил 2,6 млрд. руб.

Решение.

На основе данных можно сделать анализ сложившейся ситуации по итогам работы в 2014 г.

Фирма планировала увеличить товарооборот в 1,4 раза, или на 40%, так как ОВПЗ = 2,8/2,0 = 1,4, но план был реализован на 92,9%: ОВВП = 2,6 / 2,8 = 0,929.

Однако товарооборот фирмы вырос в 1,3 раза, или на 30% по сравнению с 2013 г:

ОВД = ОВПЗ * ОВВП = 1,4 * 0,929 = 1,3.

ОВС - ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА СТРУКТУРЫ

Отношение части к целому

Применяется для характеристики структуры явления

Выражается в коэффициентах или процентах

ДЛЯ ХАРАКТЕРИСТИКИ В ПРОСТРАНСТВЕ

 ОВСр - относительная величина сравнения

Показатель, характеризующий объект А Показатель, характеризующий объект Б

Соотношение одноименных абсолютных показателей, характеризующих разные объекты (организации, области, страны и т.д.) или территории, но соответствующих одному и тому же периоду или

моменту времени

Выражается в коэффициентах или процентах

12.09.2016

ДЛЯ ХАРАКТЕРИСТИКИ СОСТАВА И ВНУТРЕННИХ СВЯЗЕЙ ЯВЛЕНИЯ

 ОВС - относительная величина структуры

Характеризует структуру совокупности и показывает, какую долю (или удельный вес) во всей совокупности составляет отдельная ее часть: удельный вес женщин, малых предприятий, частных предприятий

Удельный вес части совокупности в общем ее объеме:

ОВС = fi / Σ fi * 100%,

где fi - количество единиц части совокупности Σ fi - общий объем совокупности

ДЛЯ ХАРАКТЕРИСТИКИ СОСТАВА И ВНУТРЕННИХ СВЯЗЕЙ ЯВЛЕНИЯ

 ОВК - относительная величина координации

Характеризует отношение частей совокупности к одной из них, взятой за базу сравнения

Вкачестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или иной точки зрения:

ОВК = fi / fj * 1000,

где fi - количество единиц i-части совокупности fj - количество единиц j-части совокупности

Показывает, во сколько раз одна часть совокупности больше другой или сколько единиц одной части приходится на 1, 10, 100, 1000, 10000 единиц другой части

ДЛЯ ХАРАКТЕРИСТИКИ В ПРОСТРАНСТВЕ

ОВИ - относительная величина интенсивности

Характеризует степень распространения или развития какого-либо явления в присущей ему среде

Показатель, характеризующий среду распространения явления А

Выражается в процентах, промилле, продецимилле или имеет другую единицу измерения (плотность населения, производительность труда, себестоимость единицы продукции)

ДЛЯ ХАРАКТЕРИСТИКИ В ПРОСТРАНСТВЕ

ОВИ - относительная величина интенсивности

Определяются сопоставлением разноименных, но связанных между собой абсолютных величин: фондоотдача, фондоемкость, плотность населения на 1 км2, число автомашин на сто семей и т. д.

Разновидность показателей ОВИ - относительные

показатели уровня экономического развития

характеризуют размеры производства различных видов продукции на душу населения (среднедушевой уровень производства)

Относительные величины не заменяют абсолютных величин, которые с их помощью сравниваются

Лишь комплексное применение абсолютных и относительных величин позволяет наглядно и всесторонне охарактеризовать количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной

Однако совместное использование абсолютных и относительных величин требует соблюдения условий их сопоставимости

ЛЕКЦИЯ 10

Понятие средних величин, их виды и способы получения

УСЛОВИЯ ПРАВИЛЬНОГО ПРИМЕНЕНИЯ СРЕДНЕЙ ВЕЛИЧИНЫ

должна исчисляться лишь для совокупностей, состоящих из однородных единиц

совокупность, неоднородную в качественном отношении, необходимо разделять на однородные группы и вычислять для них групповые типичные средние, характеризующие каждую из этих групп

сглаживает индивидуальные значения и тем самым может элиминировать различные тенденции в развитии, скрыть передовое и отстающее, поэтому кроме средней величины следует исчислять другие показатели

целесообразно исчислять не для отдельных единичных фактов, взятых изолированно друг от друга, а для совокупности фактов

Виды средних величин

12.09.2016

ВИДЫ СРЕДНИХ ВЕЛИЧИН

Средние величины делятся на две основные категории в зависимости от поставленной цели исследования, вида и взаимосвязи изучаемых признаков:

степенные средние

структурные средние

Выбор того или иного вида средней производится в зависимости от цели исследования, экономической сущности и характера усреднения исходных данных

ВИДЫ И ЭЛЕМЕНТЫ СТЕПЕННОЙ СРЕДНЕЙ

Элементы степенной средней

(x)единиц (n) частоты (f)

ВИДЫ СТЕПЕННОЙ СРЕДНЕЙ

Формулы степенных средних включают показатель степени (k)

В зависимости от его значения различают виды средних

Средняя гармоническая (k = -1)

Средняя геометрическая (k = 0)

Средняя арифметическая (k = 1)

Средняя квадратическая (k = 2)

Средняя кубическая (k = 3)

Средняя биквадратическая (k = 4)

ПРАВИЛО МАЖОРИТАРНОСТИ

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми

Правило мажоритарности: с увеличением показателя степени увеличивается и соответствующая средняя величина

СРЕДНЯЯ ГАРМОНИЧЕСКАЯ (K = -1) ПРИМЕНЯЕТСЯ, ЕСЛИ ИЗВЕСТНЫ ВАРЬИРУЮЩИЕ ОБРАТНЫЕ ЗНАЧЕНИЯ ПРИЗНАКА

Средняя гармоническая простая –

величина обратная средней арифметической

простой n X

1x

Средняя гармоническая взвешенная

используется при отсутствии действительных носителей признака

Например, предприятия А, В, С произвели продукции на 102%, 104%, 98%. Средняя арифметическая величина объективно не будет соответствовать состоянию дел, поэтому необходимо использовать среднегармоническую величину

X W где W – вес или произведение x·* f =

Wx W

СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ (K = 1) ПРИМЕНЯЕТСЯ В ТЕХ СЛУЧАЯХ, КОГДА ОБЪЕМ ВАРЬИРУЮЩЕГО ПРИЗНАКА ДЛЯ ВСЕЙ СОВОКУПНОСТИ ОБРАЗУЕТСЯ КАК СУММА ЗНАЧЕНИЙ ПРИЗНАКА ОТДЕЛЬНЫХ ЕЕ ЕДИНИЦ

Средняя арифметическая величина

представляет собой самый распространенный вид средней величины

Используется в расчете индекса Доу-Джонса, среднего остатка оборотных средств по балансу, среднегодовой численности населения и др.

X x n

где x – индивидуальные значения признака отдельных единиц совокупности

n – численность совокупности

12.09.2016

ПОРЯДОК ВЫБОРА ВИДА СРЕДНЕЙ ВЕЛИЧИНЫ КАЧЕСТВЕННОГО ПРИЗНАКА

Если известны численные значения знаменателя формулы, а значения числителя не известны, но могут быть найдены как произведение двух взаимосвязанных показателей, для одного из которых вычисляется средняя, то средняя вычисляется по формуле средней

арифметической

Если известны численные значения числителя формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя вычисляется по формуле средней гармонической

Если известны численные значения числителя и знаменателя формулы показателя, то средняя вычисляется непосредственно по этой формуле

СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ (К = 0) ШИРОКО ПРИМЕНЯЕТСЯ ДЛЯ ОПРЕДЕЛЕНИЯ СРЕДНИХ ТЕМПОВ ИЗМЕНЕНИЯ В РЯДАХ ДИНАМИКИ,

АТАКЖЕ В РЯДАХ РАСПРЕДЕЛЕНИЯ

Средняя геометрическая простая применяется для исчисления средних темпов роста показателей

за различные промежутки времени: биржевой индекс

«Файнэншнл Таймс», сложные проценты на рынке ценных бумаг, среднегодовой коэффициент роста

Xnx1 x2 xn

Средняя геометрическая взвешенная

применяется, когда темпы роста остаются неизменными в течение нескольких периодов

X геом. f П (xf )

где П(xf) - произведение

f –продолжительность отрезков времени

Средняя арифметическая взвешенная величина используется в случаях, когда расчет осуществляется по сгруппированным данным или вариационным рядам

При расчете суммирование одного из повторяющихся вариантов заменяется на частоту своего повторения

При этом величина средней зависит от соотношения их весов. Чем больше веса имеют малые значения вариантов, тем меньше величина средней, и наоборот

где f – частота

Эта формула используется при расчете среднего балла успеваемости студентов, для расчета фондового индекса «Стендарт энд пурз – 500», в расчетах экономических показателей

Средняя квадратическая (k = 2)

Средняя кубическая (k = 3)

Средняя биквадратическая (k = 4)

Структурные характеристики

ряда распределения

медиана квартили децили процентили

МОДА НАИБОЛЕЕ ЧАСТО ВСТРЕЧАЮЩАЯСЯ В СОВОКУПНОСТИ ВЕЛИЧИНА ВАРИАНТА

Например, ряд 2, 4, 3,3, 3, 3, 1, 5. Мо = 3

В практике мода и медиана часто используются вместо средней арифметической или наряду с ней.

Фиксируя цены на оптовых рынках, записывают наиболее часто встречающуюся цену каждого продукта (моду цены)

Тем не менее, наилучшей характеристикой величины варианта служит средняя арифметическая, которая имеет ряд существенных преимуществ, главное из которых – точное отражение суммы всех значений признака, использующихся для решения соответствующих практических задач

12.09.2016

СТРУКТУРНЫЕ (НЕПАРАМЕТРИЧЕСКИЕ) СРЕДНИЕ

Кроме степенных средних, когда определяется некая абстрактная величина, могут быть использованы величины конкретных вариантов имеющихся в рассматриваемой совокупности величин, величин занимающих определенное место в ранжированном ряду индивидуальных значений признака – структурные средние

Ранжировка признаков может быть построена в порядке возрастания или убывания индивидуальных значений признака

Структурные средние используют для изучения внутреннего строения последовательности и структуры рядов распределения значений признака

КВАНТИЛИ РАСПРЕДЕЛЕНИЯ ПРЕДСТАВЛЯЮТ СОБОЙ ОБОБЩАЮЩИЕ ПОКАЗАТЕЛИ, ХАРАКТЕРИЗУЮЩИЕ СТРУКТУРУ РАСПРЕДЕЛЕНИЯ ПРИЗНАКА В СОВОКУПНОСТИ

Квантиль – это значение признака Х, занимающее определенное место в упорядоченной по данному признаку совокупности

Виды квантилей:

медиана (Ме) – значение признака, приходящееся на середину упорядоченной совокупности

квартили (Q1/4 ,Q2/4 = Ме, Q3/4) - значение признака, делящее упорядоченную совокупность на 4 равные части

децили (Q0,1, Q0,2, …, Q0,9) - значение признака, делящее упорядоченную совокупность на 10 равных частей

процентили (Q0,01, Q0,02, …, Q0,09) - значение признака, делящее упорядоченную совокупность на 100 равных частей

МЕТОДИКА РАСЧЕТА СТРУКТУРНЫХ СРЕДНИХ Мода

В вариационном дискретном ряду модой

выступает варианта, имеющая наибольшую частоту или частость

В интервальных рядах с равными интервалами мода - это значение признака, которому соответствует наибольшая плотность распределения и вычисляется:

где X0 — минимальная граница модального интервала i - величина модального интервала

fm - частота модального интервала

fm-1 - частота интервала, предшествующего модальному интервалу fm+1 - частота интервала, следующего за модальным.

Модальный интервал в интервальном ряду определяется по наибольшей частоте

МОДА

Если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды

Если две несоседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называют бимодальным

если таких вариант больше двух, то ряд - полимодальный

КВАНТИЛИ РАСПРЕДЕЛЕНИЯ

Медиана - варианта, которая находится в середине вариационного ряда

Медиана делит ряд пополам, по обе стороны от нее находится одинаковое количество единиц совокупности

Вранжированных рядах несгруппированных данных медиана равна значению признака, расположенного строго в середине ряда

Вдискретном вариационном ряду определение

медианного значения признака сводится к определению номера медианной единицы ряда:

где n - объем совокупности

ГРАФИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ МЕДИАНЫ ПО КУМУЛЯТЕ РАСПРЕДЕЛЕНИЯ

Последнюю ординату кумуляты делят пополам. Через полученную точку проводят прямую, параллельную оси х, до пересечения ее с кумулятой. Из точки пересечения опускается перпендикуляр до оси абсцисс. Абсцисса точки пересечения является медианой

12.09.2016

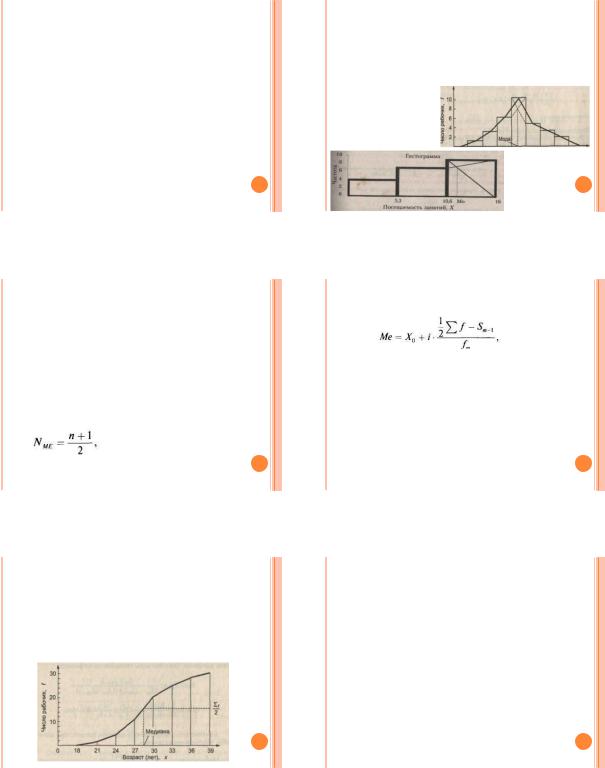
ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ МОДЫ РАВНОИНТЕРВАЛЬНОГО РЯДА ПО ГИСТОГРАММЕ РАСПРЕДЕЛЕНИЯ

Правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника - с левым верхним углом последующего прямоугольника

Абсцисса точки пересечения этих прямых и будет модой распределения

В интервальном ряду с равными интервалами

медиана рассчитывается по формуле

где X0 - начальное значение медианного интервала; i - величина медианного интервала

Σ f - сумма частот ряда

S m-1 - сумма накопленных частот в интервалах, предшествующих медианному

fm - частота медианного интервала

Для определения медианного интервала

необходимо рассчитать суммы накопленных частот Медианный интервал характерен тем, что его кумулятивная частота равна полусумме всех частот ряда или превышает ее

КВАРТИЛЬ - ЗНАЧЕНИЯ ПРИЗНАКА, ДЕЛЯЩИЕ РАНЖИРОВАННУЮ СОВОКУПНОСТЬ НА ЧЕТЫРЕ РАВНЫЕ ЧАСТИ

Нижний квартиль (Q1), отделяющий 1/4 часть совокупности с наименьшими значениями признака

Верхний квартиль (Q3), отсекающий 1/4 часть с наибольшими значениями признака

Средний квартиль (Q2) совпадает с медианой

(Me)