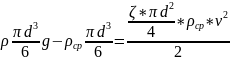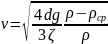- •Первые вопросы
- •Механизмы переноса массы. Молекулярная и конвективная плотность потока массы.
- •Построение рабочих линий:
- •Флегмовое число .
- •Флегмовое число – минимально ( .
- •Построение рабочих линий:
- •22. Составьте уравнения материального баланса при разделении суспензий и выведите уравнение для расчета площади поверхности осаждения.
- •23. Основные параметры, характеризующие зернистый слой. Получите выражения для расчета эквивалентного диаметра через удельную поверхность и диаметр частиц.
- •24. Поясните принцип расчета скорости начала псевдоожижения из зависимости р неподвижного слоя от определяющих параметров.
- •Вторые вопросы
- •Расчет на основе уравнения массопередачи
- •Осаждение под действием сил тяжести (отстаивание)
- •Разделение в циклонах, отстойное центрифугирование
- •Электроочистка
- •Охарактеризуйте состояние зернистого слоя в зависимости от скорости восходящего потока газа или жидкости. Изобразите зависимости гидравлического сопротивления и высоты слоя от скорости потока.
- •Основные способы очистки газов от пыли. Охарактеризуйте каждый из способов, укажите области применения.
- •Электрические методы очистки:
- •Третьи вопросы
- •Достоинства:
- •Изобразите схему устройства и опишите принцип действия абсорбционной колонны с клапанными тарелками. Достоинства и недостатки этих тарелок.
- •Изобразите схему устройства и опишите принцип действия абсорбционной колонны с колпачковыми тарелками. Достоинства и недостатки этих тарелок.
- •Изобразите схему устройства и опишите принцип действия распылительного абсорбера. Достоинства и недостатки этого абсорбера по сравнению с барботажным абсорбером.
- •Изобразите схему устройства и опишите действие установки для непрерывной ректификации бинарных жидких смесей.
- •Изобразите схему устройства и опишите действие барабанного вакуум – фильтра. Сопоставьте с другими фильтрами для разделения суспензии.
- •Изобразите схему устройства и опишите действие фильтрующей центрифуги. Сопоставьте с другими фильтрами для разделения суспензии.
- •Изобразите схему устройства и опишите действие рукавного фильтра. Сопоставьте с другими пылеочистительными аппаратами.
- •Изобразите схему устройства и опишите действие одноярусного гребкового непрерывно действующего отстойника. Сравните с другими аппаратами для разделения гетерогенных систем.
- •Изобразите схему устройства и опишите действие циклона. Сопоставьте с другими аппаратами для разделения гетерогенных систем.
- •Изобразите схему устройства и опишите действие батарейного циклона. Сопоставьте с другими аппаратами для разделения гетерогенных систем.
- •Изобразите схему устройства и опишите действие гидроциклона. Сопоставьте с другими аппаратами для разделения гетерогенных систем.
- •Изобразите схему устройства и опишите действие электрофильтра. Область применения данного устройства.
- •Изобразите схему устройства и опишите действие барботажного пылеуловителя. Сопоставьте с другими аппаратами для разделения гетерогенных систем.
Флегмовое число .
Поскольку
 , то значение
означает, что либо
, то значение
означает, что либо
 ,
либо
,
либо
 .
Рассмотрим более реальный вариант :
.
Рассмотрим более реальный вариант :
Проанализируем уравнение рабочей линии верхней части колонны:
При отрезок, отсекаемый продолжением линии на оси ординат равен 0, то есть рабочая линия должна совместиться с диагональю диаграммы.
Из
уравнения материального баланса для
установки по всей жидкой фазе
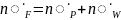 следует, что при
следует, что при
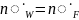 ,
то есть жидкая фаза выходит из установки
только в виде так называемого «кубового
остатка». При этом из уравнения:
,
то есть жидкая фаза выходит из установки
только в виде так называемого «кубового
остатка». При этом из уравнения:
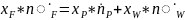
Следует,
что
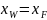 ,
то есть разделения смеси на выходе из
установки нет!
,
то есть разделения смеси на выходе из
установки нет!
Таким
образом, на фазовой диаграмме точка
 должна сместиться и слиться с точкой
.
В результате нет рабочей линии нижней
части колонны! Во всех сечениях нижней
часть колонны составы жидкости одинаковы
: [
должна сместиться и слиться с точкой
.
В результате нет рабочей линии нижней
части колонны! Во всех сечениях нижней
часть колонны составы жидкости одинаковы
: [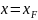 ]
, неизменны и составы пара [
]
, неизменны и составы пара [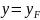 ].
].
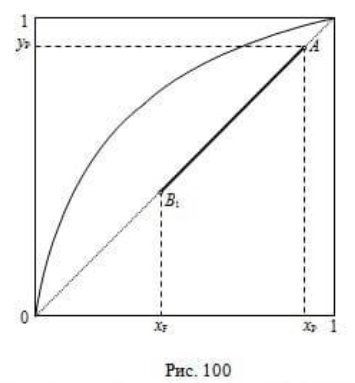
В этом случае движущая сила массопередачи в каждом сечении аппарата максимальна, а число теоретических ступеней изменения концентрации ( или теоретических тарелок) – минимально. Минимальному числу ступеней разделения будет соответствовать и минимальная рабочая линия высота аппарата. Однако увеличение расхода жидкой фазы должно сопровождаться увеличением диаметра аппарата ( во избежание захлёбывания).
Флегмовое число – минимально ( .
В
предельном случае, при минимальном
флегмовом числе, точка пересечения
рабочих линий совпадает с линией
равновесия идеальных бинарных систем
( т.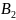 на рис. ниже).
на рис. ниже).

Теперь
в точке
движущая сила равна нулю; число
теоретических ступеней
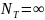 ,
то есть потребуется бесконечно большая
высота аппарата за счёт бесконечно
большой площади поверхности фазового
контакта. Но при минимальном расходе
жидкости минимальным должен быть и
диаметр аппарата.
,
то есть потребуется бесконечно большая
высота аппарата за счёт бесконечно
большой площади поверхности фазового
контакта. Но при минимальном расходе
жидкости минимальным должен быть и
диаметр аппарата.
Построение рабочих линий:
Изначально
нам известны: концентрация НК в исходной
смеси «
»,
требуемая концентрация этого компонента
в продукте (дистилляте) «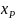 »,
и допустимое содержание компонента в
кубовом остатке «
»,
Следовательно, имеем 3 точки на оси
абсцисс.
»,
и допустимое содержание компонента в
кубовом остатке «
»,
Следовательно, имеем 3 точки на оси
абсцисс.
По допущениям 5 и 6 ( и . Следовательно, имеем 2 точки на оси ординат.
Последнее позволяет отобразить 2 крайние точки (А и С) 2-х рабочих линий: точки на диагонали диаграммы, т.е. на линии равенства концентраций в жидкой и в паровой фазах. Будем считать, что флегмовое число известно. Из уравнения рабочей линии укрепляющей части колонны получаем:
, что представляет собой отрезок на оси ординат, отсекаемый продолжением рабочей линии (прямой!) укрепляющей части колонны.
По двум точкам определяем направление рабочей линии, а сама рабочая линия ограничена значениями концентраций компонента в жидкой фазе: « » на верху колонны и « » - в точке питания. Отрезок АВ есть изображение рабочей линии верхней части колонны. Точка В одновременно принадлежит и рабочей линии нижней, исчерпывающей части колонны. Наличие 2-х точек ( В и С) достаточно, чтобы провести прямую рабочую линию ВС нижней части колонны.
18. Выведите формулу для расчёта минимального флегмового числа при непрерывной ректификации. Объясните зависимость между флегмовым числом, размерами колонны и расходом теплоты при ректификации. Каковы критерии выбора оптимального флегмового числа?
Чтобы получить расчётную формулу, воспользуемся уравнением рабочей линии верхней части колонны :
В
рассматриваемом случае нам точно
известны концентрации фаз не только в
точке А рабочей линии, но и в точке
:
при
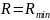 ,
, а
,
, а
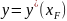 .
Следовательно,
.
Следовательно,

Откуда
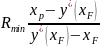 .
.
Зависимость между флегмовым числом, размерами колонны и расходом теплоты:
.
При рабочие линии совпадают с диагональю диаграммы и движущая сила процесса является наибольшей, а необходимое число теоретических ступеней . Количество действительных ступеней разделения пропорционально числу теоретических ступеней. Таким образом, при потребовалась бы наименьшая рабочая высота колонны. С увеличением R возрастает количество жидкости, которое необходимо испарить в кипятильнике. При требуется испарить максимально возможное количество жидкости. Следовательно, в этом случае расход греющего пара наибольший.
При
, когда рабочие линии пересекаются с
линией равновесия, в точке пересечения
движущая сила равна нулю. Значит, для
того чтобы достигнуть концентраций
фаз, соответствующих их составам на
питающей тарелке, потребовалась бы
бесконечно большая поверхность контакта
фаз, т. е. бесконечно большое число
«ступенек» – теоретических ступеней
разделения. Таким образом, при
 разделение возможно только в гипотетической
ректификационной колонне
бесконечно большой высоты.
При этом расход греющего пара, которые
при прочих равных условиях пропорционален
флегмовому числу, т. к.
разделение возможно только в гипотетической
ректификационной колонне
бесконечно большой высоты.
При этом расход греющего пара, которые
при прочих равных условиях пропорционален
флегмовому числу, т. к.
 ,
будет наименьший.
,
будет наименьший.
На практике действительное флегмовое число R должно быть, конечно же, больше минимального. Оно должно быть оптимальным относительно каких-либо критериев. Так, например, критерием оптимальности может служить величина рабочего объема аппарата. Объем аппарата, естественно, должен быть минимальным. При нахождении оптимального флегмового числа обычно находят минимум функции:
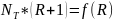 ,
где
,
где
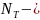 величина, пропорциональная высоте
колонны;
величина, пропорциональная высоте
колонны;
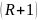 – величина,
пропорциональная расходу пара, то есть
диаметру колонны.
– величина,
пропорциональная расходу пара, то есть
диаметру колонны.
Как правило, величина оптимального флегмового числа составляет:
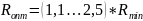
19. Выведите уравнение теплового баланса ректификационной колонны непрерывного действия. Как определяется расход греющего пара в кипятильнике? Как определяется расход теплоносителя в дефлегматоре?
Для колонны непрерывного действия с учетом потерь тепла в окружающую среду имеем:
Приход тепла:
С теплоносителем в кипятильнике
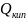 ;
;С исходной смесью
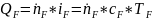 ;
;C флегмой
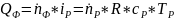 .
.
Расход тепла:
С парами, поступающими из колонны в дефлегматор:
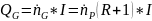
С кубовым остатком:

Потери в окружающую среду -
 ,
,
Где
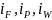 -
удельные энтальпии исходной смеси,
дистиллята и кубового остатка
соответственно
-
удельные энтальпии исходной смеси,
дистиллята и кубового остатка
соответственно
I - удельная энтальпия пара, выходящего из колонны;
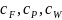 -
изобарные теплоемкости исходной смеси,
дистиллята и кубового остатка,
соответственно;
-
изобарные теплоемкости исходной смеси,
дистиллята и кубового остатка,
соответственно;
T – температуры.
Запишем уравнение теплового баланса:
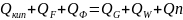
Подставляем значения Q из вышеприведенных уравнений и получим:
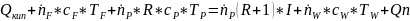
Решая уравнение (13.9) относительно , получим тепловую нагрузку
кипятильника:

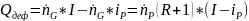
Тепловая нагрузка дефлегматора Qдеф зависит от количества поступающих в него паров:
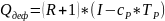
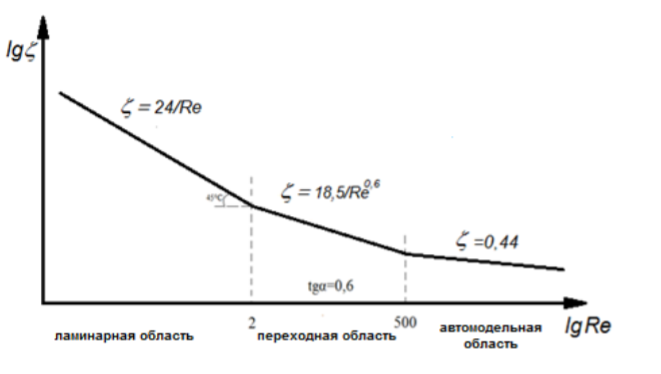
20. Гидродинамические режимы обтекания тел. Изобразите зависимость коэффициента сопротивления среды от критерия Рейнольдса при обтекании.
1.
Ламинарная область ( областьь действия
закона Стокса) характерна для осаждения
мелких частиц. В этой области гидравлическое
сопротивление осаждению пропорционально
скорости
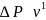 .
.
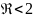
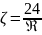
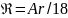

2.
Переходная область – наиболее часто
возникает при осаждении частиц. В этой
зоне гидравлическое сопротивление
осаждению возрастает быстрее, чем в
ламинарной области:

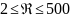
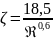
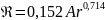

3.Автомодельная область – зона действия закона Ньютона.
В
этой области гидравлическое сопротивление
осаждению пропорционально квадрату
скорости
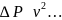 Коэффициент
сопротивления не зависит от скорости
Коэффициент
сопротивления не зависит от скорости
Re>500
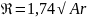
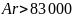
Для тел не шарообразной формы сопротивление больше, чем для шарообразной.
Зависимость коэффициента сопротивления от критерия Рейнольдса:
21. Осаждение под действием силы тяжести. Силы, действующие на частицу. Выведите уравнение для определения скорости свободного осаждения шарообразной частицы.
Осаждение под действием сил тяжести (отстаивание)
Кинетика осаждения.
Сопротивление сред движущемуся телу зависит от формы тела и режима его обтекания. При ламинарном движении тело окружено пограничным слоем жидкости. Слои жидкости плавно обтекают тело. С увеличением скорости осаждения пограничный слой начинает отрываться от поверхности тела. За двигающимся телом понижается давление и образуется завихрения. Таким образом, образуется разность давлений на лобовую и кормовую поверхности, и она больше, чем при ламинарном обтекании. При дальнейшем увеличении критерия Re наступает такая область, в которой лобовое сопротивление становится преобладающим и сопротивлением трения можно пренебречь. Наступает автомодельный режим, в котором сопротивление не зависит от скорости.
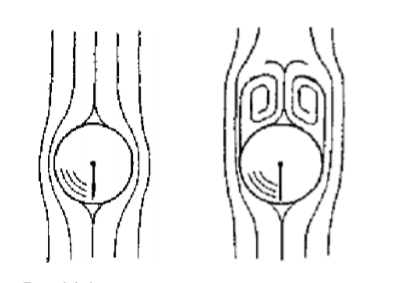
Сила
сопротивления среды
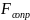 пропорциональна сечению частицы
пропорциональна сечению частицы
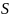 и квадрату скорости осаждения
и квадрату скорости осаждения
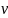 :
:
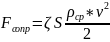 ,
,
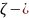 коэффициент
сопротивления.
коэффициент
сопротивления.
Скорость осаждения частицы постоянна, т.к. частиц сила тяжести частицы в среде уравновешивается силой сопротивления:
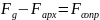
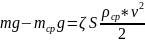
Где
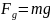 -
сила тяжести,
-
сила тяжести,
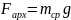 – сила выталкивания, m-
масса частицы,
– сила выталкивания, m-
масса частицы,
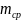 -
масса среды в объеме частицы, ρ- плотность
частицы,
-
масса среды в объеме частицы, ρ- плотность
частицы,
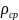 -
плотность среды.
-
плотность среды.
Массу шарообразной частицы можно записать как:
 ,
d-
диаметр
частицы.
,
d-
диаметр
частицы.
Подставим выражения для действующих на частицу сил и сечения частицы S: