
- •Первые вопросы
- •Механизмы переноса массы. Молекулярная и конвективная плотность потока массы.
- •Построение рабочих линий:
- •Флегмовое число .
- •Флегмовое число – минимально ( .
- •Построение рабочих линий:
- •22. Составьте уравнения материального баланса при разделении суспензий и выведите уравнение для расчета площади поверхности осаждения.
- •23. Основные параметры, характеризующие зернистый слой. Получите выражения для расчета эквивалентного диаметра через удельную поверхность и диаметр частиц.
- •24. Поясните принцип расчета скорости начала псевдоожижения из зависимости р неподвижного слоя от определяющих параметров.
- •Вторые вопросы
- •Расчет на основе уравнения массопередачи
- •Осаждение под действием сил тяжести (отстаивание)
- •Разделение в циклонах, отстойное центрифугирование
- •Электроочистка
- •Охарактеризуйте состояние зернистого слоя в зависимости от скорости восходящего потока газа или жидкости. Изобразите зависимости гидравлического сопротивления и высоты слоя от скорости потока.
- •Основные способы очистки газов от пыли. Охарактеризуйте каждый из способов, укажите области применения.
- •Электрические методы очистки:
- •Третьи вопросы
- •Достоинства:
- •Изобразите схему устройства и опишите принцип действия абсорбционной колонны с клапанными тарелками. Достоинства и недостатки этих тарелок.
- •Изобразите схему устройства и опишите принцип действия абсорбционной колонны с колпачковыми тарелками. Достоинства и недостатки этих тарелок.
- •Изобразите схему устройства и опишите принцип действия распылительного абсорбера. Достоинства и недостатки этого абсорбера по сравнению с барботажным абсорбером.
- •Изобразите схему устройства и опишите действие установки для непрерывной ректификации бинарных жидких смесей.
- •Изобразите схему устройства и опишите действие барабанного вакуум – фильтра. Сопоставьте с другими фильтрами для разделения суспензии.
- •Изобразите схему устройства и опишите действие фильтрующей центрифуги. Сопоставьте с другими фильтрами для разделения суспензии.
- •Изобразите схему устройства и опишите действие рукавного фильтра. Сопоставьте с другими пылеочистительными аппаратами.
- •Изобразите схему устройства и опишите действие одноярусного гребкового непрерывно действующего отстойника. Сравните с другими аппаратами для разделения гетерогенных систем.
- •Изобразите схему устройства и опишите действие циклона. Сопоставьте с другими аппаратами для разделения гетерогенных систем.
- •Изобразите схему устройства и опишите действие батарейного циклона. Сопоставьте с другими аппаратами для разделения гетерогенных систем.
- •Изобразите схему устройства и опишите действие гидроциклона. Сопоставьте с другими аппаратами для разделения гетерогенных систем.
- •Изобразите схему устройства и опишите действие электрофильтра. Область применения данного устройства.
- •Изобразите схему устройства и опишите действие барботажного пылеуловителя. Сопоставьте с другими аппаратами для разделения гетерогенных систем.
Первые вопросы
Механизмы переноса массы. Молекулярная и конвективная плотность потока массы.
Механизмы переноса внутри фазы:
молекулярный (диффузионный), осуществляется перемещением молекул вещества (в неподвижных ламинарно движущихся средах).
конвективный, осуществляется перемещением макрочастиц (перенос потоком). Конвективный перенос осуществляется значительно быстрее диффузионного.
![]()
Перенос массы по молекулярному механизму (диффузия) подчиняется первому закону Фика:

В
случае конвективного переноса массы:
![]()
Таким образом, в случае молекулярного и конвективного переноса массы общая плотность потока массы или энергии складывается из двух векторных величин:
![]()
Выведите дифференциальное уравнение конвективной диффузии, указав соответствующие допущения. Приведите уравнение для диффузии в неподвижной среде. С какой целью используется данное уравнение при изучении массообменных процессов?
Это
уравнение является частным случаем
уравнения:
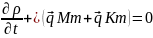 при постоянной плотности (общей
концентрации)
при постоянной плотности (общей
концентрации)
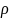 ,
постоянном коэффициенте диффузии D
и отсутствии объемных источников
(стоков) массы R=0,
которые возникают в результате химической
реакции в рассматриваемом объеме, т.е.
,
постоянном коэффициенте диффузии D
и отсутствии объемных источников
(стоков) массы R=0,
которые возникают в результате химической
реакции в рассматриваемом объеме, т.е.
Т.к.
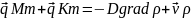 ,
то
,
то
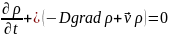
При D=const :
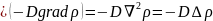
Где
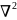 – оператор Лапласа.
– оператор Лапласа.
Дивергенцию
от (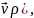 как
произведения векторной и скалярной
величины можно представить в виде:
как
произведения векторной и скалярной
величины можно представить в виде:
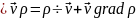
Тогда:
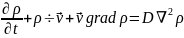
Для случая = const (несжимаемые среды) с учетом уравнения неразрывности:

Соотношение принимает следующую форму:
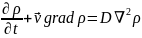
Разделив
каждый член уравнения на молярную массу
распределяемого компонента (М –
постоянная величина), с учетом
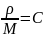 –
объемная мольная концентрация будем
иметь:
–
объемная мольная концентрация будем
иметь:
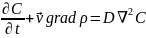
Уравнение выше: уравнение конвективной диффузии.
Допущения: постоянная плотность (общая концентрациия) , постоянный коэффициент диффузии D и отсутствии объемных источников (стоков) массы R=0.
Цель использования: диф уравнение конвективной диффузии описывает в общем виде распределение концентраций в движущейся жидкости (с учетом принятых допущений).
Получите определяющие массообменные критерии подобия из дифференциального уравнения конвективной диффузии. Физический смысл массообменных критериев подобия.








Приведите уравнение массоотдачи, укажите движущую силу массоотдачи, коэффициент массоотдачи. Получите определяющий массообменный критерий Шервуда, поясните его физический смысл.
Критерий Шервуда показывает соотношение между потоком вещества, переносимым совместно конвекцией и диффузией в ядре потом и молекулярной диффузией в пограничном слое. Уравнение массоотдачи и вывод Шервуда скринами выше.
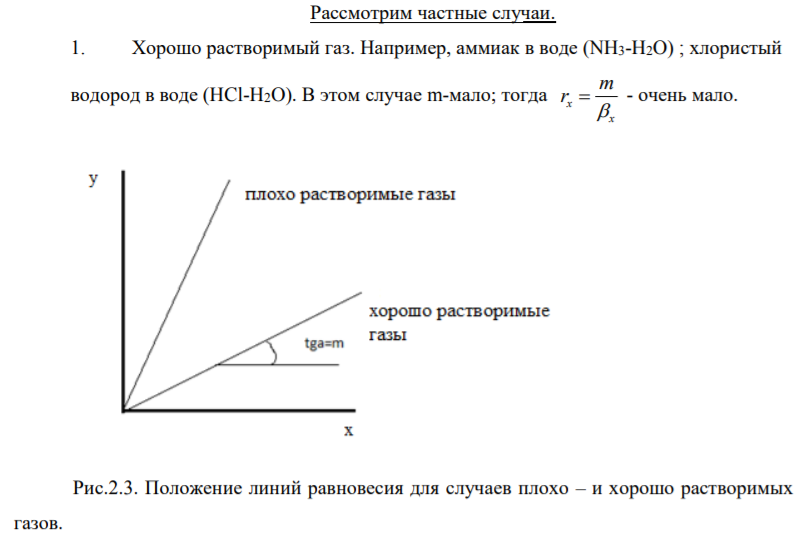
5. На основе аддитивности диффузионных сопротивлений получите уравнение для расчета коэффициента массопередачи, указав соответствующие допущения. Что является лимитирующей стадией массопередачи для плохо- и хорошо растворимых газов при абсорбции?
Допущения: выделим элементный участок аппарата поверхностью dA.
Масса вещества переходит из газовой фазы Фу в жидкую Фх через элементную площадку dA.
Процесс массопередачи установившийся
Коэффициенты диффузии D и коэффициенты массоотдачи β не изменяется вдоль поверхности массоотдачи.
Зависимость между равновесными концентрациями линейна y*=m(x) m – коэффициент распределения (тангенс угла наклона касательной к равновесной линии).
На границе раздела фаз устанавливается равновесие (y(гр)=m*x(гр)). Это равносильно допущению, что нет сопротивления переходу вещества из фазы в фазу.
Вывод:
Имеем
уравнение массопередачи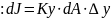
Выразим движущую силу для элемента поверхности dA как разность (y*-y)
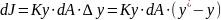
Справедливо
записать также:

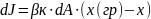
Выразим движущую силу и учтём допущения № 4 и 5:

Заменим
y*-y согласно первому уравнению системы
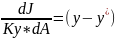 :
:
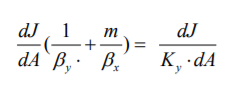
То есть:


6. Выведите уравнение материального баланса при абсорбции при противотоке газа и жидкости при условии постоянства расхода фаз. Как определяется минимальный удельный расход абсорбента?



7. Выведите линейное уравнение рабочей линии для массообменных аппаратов с непрерывным контактом фаз при противоточном движении фаз в режиме идеального вытеснения. Укажите допущения.

8. Выведите уравнения для расчета числа единиц переноса и средней движущей силы массопередачи, указав соответствующие допущения. Дайте определение числа единицы переноса.

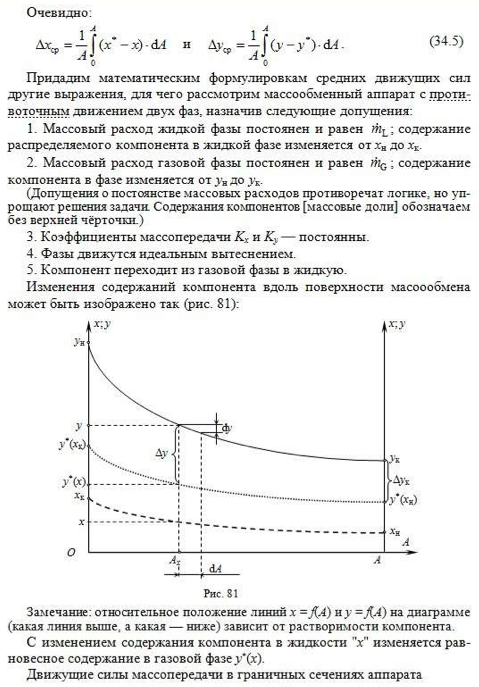



9. Приведите способы расчета высоты аппаратов с непрерывным контактом фаз. Как определяется диаметр колонн через фиктивную скорость сплошной фазы?




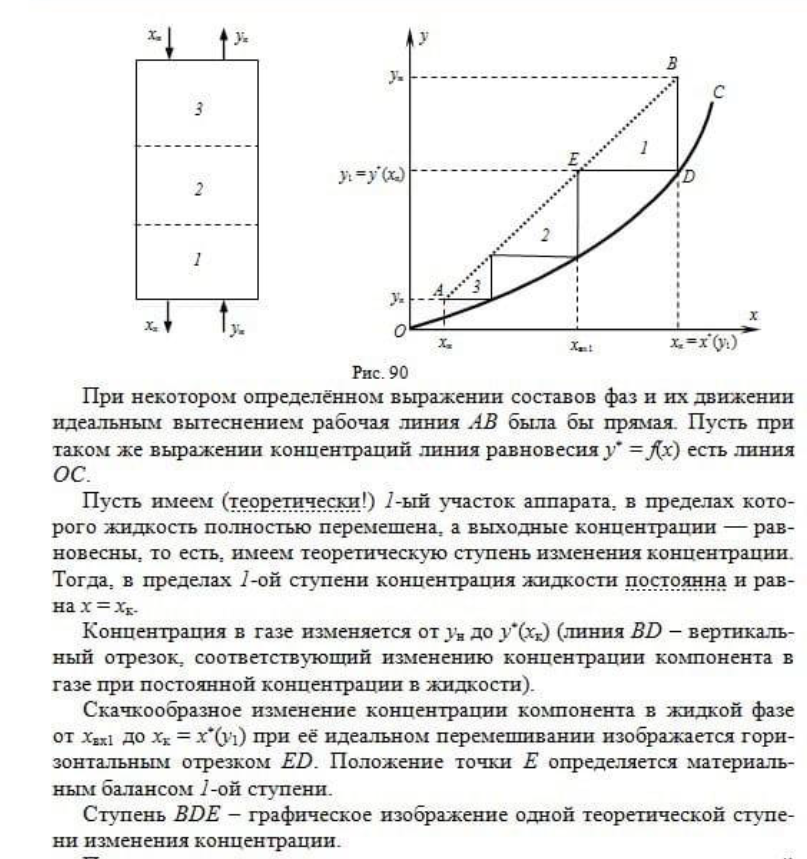


10. Определение высоты противоточных колонных аппаратов с непрерывным контактом фаз через число и высоту единиц переноса. Выведите уравнение аддитивности высот переноса массы.
11. Выведите уравнение аддитивности чисел единиц переноса массы.
12. Приведите способы расчета высоты аппаратов со ступенчатым контактом фаз. Как определяется диаметр колонн через фиктивную скорость сплошной фазы?
13. Что такое эффективность тарелки по Мэрфри и теоретическая тарелка; как они используется в расчете числа тарелок колонны высоты.

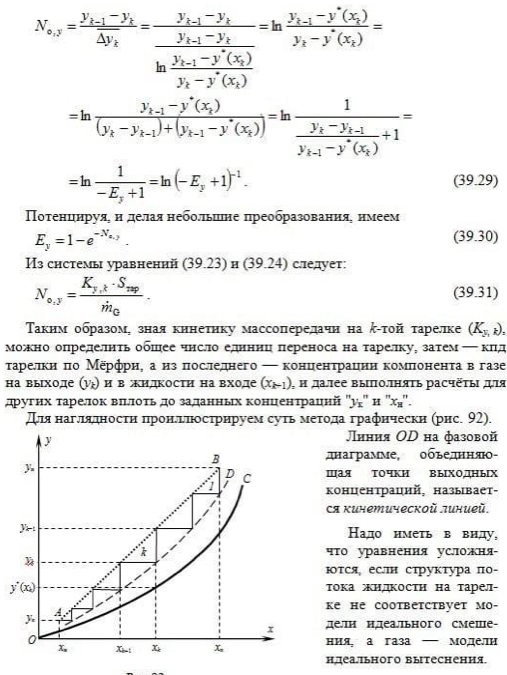
14. Выведите зависимость между эффективностью тарелки по Мэрфри и числом единиц переноса на тарелке при идеальном смешении жидкости и идеальном вытеснении газа.
Эффективность тарелки по Мёрфри ( КПД Мёрфри) : показывает долю действительного изменения концентрации на одной реальной тарелке от максимально возможного изменения на теоретической тарелке:
Эффективность
по Мёрфри:
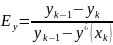
Общее
число единиц переноса на одну тарелку:

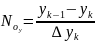
Свяжем эффективность тарелки по Мёрфри и ЧЕП:
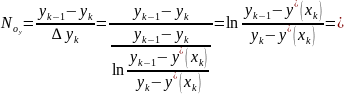
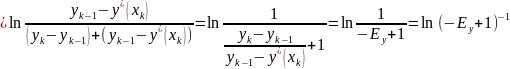
Потенцируя, и делая небольшие преобразования, имеем:

15. Получите систему уравнений материального баланса процесса простой перегонки. Расчет количества кубового остатка, количества и среднего состава дистиллята.
Пусть
изначально в куб было загружено
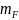 (кг)
исходной смеси. Пусть к концу процесса
было получено
(кг)
исходной смеси. Пусть к концу процесса
было получено
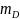 (кг) дистиллята, а в кубе осталось
(кг) дистиллята, а в кубе осталось
 кубовой жидкости.
кубовой жидкости.
Общий материальный баланс перегонки бинарных смесей представляют системой из двух уравнений, первое из которых даёт баланс по всей системе:
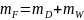 ;
а если оперировать количествами:
;
а если оперировать количествами:

а второе по низкокипящему компоненту (НК):
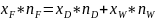
Уравнения для расчёта количества и среднего состава дистиллята можно получить на
основе уравнений материального баланса по суммарному количеству вещества и суммарному количеству НК:
Средний
состав дистиллята:
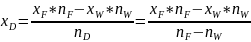 .
.
Количество
кубового остатка:
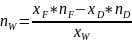
Количество
дистиллята:
 .
.
16. Выведите уравнение рабочей линии для укрепляющей части ректификационной колонны, указав соответствующие допущения. Опишите последовательность построения рабочих линий на диаграмме у–х, сформулировав необходимые допущения.
Для получения уравнений рабочих линий, необходимых для анализа процесса и расчёта аппаратов ректификации, примем следующие основные допущения:
Колонна работает без потерь вещества и теплоты.
Исходная смесь поступает в точку питания нагретой до температуры её кипения в этой точке.
Молярные теплоты испарения (конденсации) компонентов практически одинаковы.
Теплота смешения компонентов в жидкой фазе пренебрежимо мала.
Состав пара, выходящего сверху из колонны в дефлегматор, одинаков с составом флегмы, поступающей на орошение колонны.
Состав жидкости, стекающей снизу колонны в кипятильник, одинаков с составом пара, поступающим из кипятильника в колонну.
Для вывода уравнений рабочих линий сделаем дополнительное допущение: фазы движутся в насадочной колонне идеальным вытеснением.
Так как мы выводим уравнение рабочей линии верхней, укрепляющей части колонны, то достаточно составить материальный баланс участка аппарата между произвольно намеченным сечением, где составы жидкости и пара равны «х» и «у» соответственное, и верхним сечением.
Здесь флегмовым числом (R) назовем отношение расхода флегмы к расходу продукта:
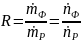
Сбалансируем приход и расход НК в намеченном объеме аппарата:
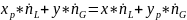
Учитывая,
что по допущению 5:
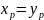 ,
получаем:
,
получаем:
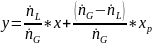
Поскольку расходы фаз постоянны, то уравнение выше есть уравнение прямой линии. В верхней части колонны расход жидкой фазы равен расходу флегмы:
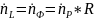
Расход пара должен быть таков, чтобы из него получить необходимое количество флегмы и , конечно же, продукта ( дистиллята), то есть
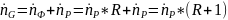
Подставляем полученные выражения для расходов фаз в уравнение прямой линии:
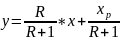
Полученное уравнение является уравнением рабочей линии укрепляющей части колонны.
