Волноводные задачи

Структуры ЭМП, возбуждаемых приземными излучателями в нижней ионосфере, представляют интерес. Некоторые особенности этой структуры будут показаны в данной работе.

Обсуждаемая проблема сводится к ряду волноводных задач (источник и приемник расположены в приземном волноводе) и к проблеме прохождения электромагнитных волн через ионосферу. Для решения волноводных задач используется модель регулярного сферического анизотропного волновода, образованного Землей и ионосферой, свойства которого зависят только от радиального направления (вводим сферическую систему координат г,9,ф с началом в центре Земли). Антенны моделируются элементарными электрическими и магнитными диполями произвольной ориентации. Для ионосферы используется приближение холодной плазмы, нелинейные эффекты не учитываются. В работе используется система СИ и зависимость от времени exp(-iwt).

Волноводные задачи сводятся к решению уравнений Максвелла для полости волновода (вакуума)

rotE = ik𝛞, rot𝛞 = —ik(E + p_e/ε₀) (1)

для электрических диполей и

rotE = ik(𝛞 + z₀p_m/μ₀), rot𝛞 = -ikE (2)

для магнитных диполей.

В уравнениях (1) и (2) p_e и p_m — объемные плотности дипольных моментов электрического и магнитного диполей, 𝛞= z₀H, а k,ε₀, μ₀ и z₀— соответственно волновое число, диэлектрическая и магнитная проницаемости и характеристический импеданс вакуума. В соответствии с принципом поляризационной двойственности общее решение уравнений Максвелла дается суперпозицией двух фундаментальных решений. Поперечно-магнитное поле описывается электрическим П_e = П_еe_r, а поперечно-электрическое магнитным П_m = П_me_r векторами Герца, направленными по координате разделения r. В области вне источников они имеют следующий вид:

𝛞 _е = —iк rotП_е, Е_е = rot rotП_е, (3)

E_m = ik rotП_m, 𝛞_т = rot rotП_m.

Граничные условия на верхней стенке волновода при r = d описываются матрицей адмиттанса ионосферы [6]. На нижней стенке при r = а зададим граничные условия, определяемые матрицей приведенного поверхностного импеданса Земли:

(4)

В выражениях (4) δ — приведенный поверхностный импеданс Земли, который полагается одинаковым для обеих поляризаций. Кроме того, должны быть выполнены условия ограниченности полей 𝛞 и Е при θ = 0, π, и условия убывания полей при при определении матрицы â.

Решение волноводной задачи для радиального электрического диполя строится методом нормальных волн (в виде разложения по собственным функциям радиального оператора) и в соответствии с принципом поляризационной двойственности описывается электрическим П_е и магнитным П_m потенциалами:

(5)

где s = 1, 2, . . . В выражении (5) Р_е — величина дипольного момента электрического диполя, а обозначения v, R^(e)_v-1/2(кr),R^(m)_v-1/2(kr),N_v-1/₂ при v = v_s соответствуют собственным значениям, собственным функциям и норме радиального оператора.

Касательные компоненты электрического и магнитного полей в полости волновода в области вне источников можно найти, дифференцируя потенциалы по координатам в соответствии с (4). Радиальные компоненты полей удобно найти, используя решение спектральной задачи:

(6)

где П_еs, П_ms - отдельные члены рядов (5).

Решение волноводных задач для источников других типов опирается на решение для радиального электрического диполя. В случае радиального магнитного диполя используется сформулированный нами принцип перестановочной двойственности для анизотропных сред [1,3], который позволяет построить решение с помощью элементарных перестановок параметров в выражениях для компонент полей радиального электрического диполя. Поля горизонтального (касательного к границам раздела) электрического диполя можно найти, применяя обобщенную теорему взаимности для магнитоактивной среды [7], которую запишем в удобном для нашей задачи виде:

(7)

При этом абсолютные значения дипольных моментов в теореме взаимности для двух электрических диполей полагаются одинаковыми и обозначаются Р_е, как и аналогичные значения для магнитных диполей Р_m; величина g равна g = Z₀ Р_еР_m^-1 . В выражениях (7) r₁ и r₂ — две любые пространственные точки. Индексы е и m у компонент полей относятся к электрическим и магнитным диполям соответственно, так что Е_Ɛ^eζ (r₁, r₂, Н₀), 𝛞_Ɛ^eζ (r_1, r₂, Н₀), например, — Ɛ-компоненты полей, создаваемые в точке r₂ расположенным точке r₁ электрическим диполем с дипольным моментом Р_е, ориентированным вдоль орта e_ζ (Ɛ,ζ = r,θ,φ).

Радиальные компоненты электрического (магнитного) поля горизонтального электрического диполя можно найти, используя теоремы взаимности для такого диполя и вспомогательного радиального электрического (магнитного) диполя. Далее с помощью выражения (6) находятся потенциалы, с помощью которых, определяются касательные компоненты электрического и магнитного полей. Аналогично находится поля горизонтального магнитного диполя.

Что касается задачи прохождения волн через сферически слоистую ионосферу, то асимптотическое разделение переменных в уравнениях Максвелла с тензором относительной комплексной диэлектрической проницаемости ионосферы _m ­ позволяет свести их к системе четырех связанных обыкновенных дифференциальных уравнений первого порядка с переменными коэффициентами для касательных компонент электрического и магнитного полей.

(8)

По форме система похожа на ту, которая описывают прохождение плоских волн через однородную среду [6]. Отличие заключается в том, что свойства среды и угол падения волны на ионосферу зависят от радиальной координаты.

Рис. 2. Зависимости |E_ɛ (H)| и |𝛞_ɛ (H)| для mθ диполя, день, 10кГц

Из четырех линейно незави­симых решений граничным условиям при 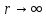от удовлетворяют два, которые позволяют ввести матричный адмиттанс и получить для его элементов систему дифференци­альных уравнений. Адмиттанс несет в себе информацию об обоих линейно независимых решениях, так что для вычисления, â = â(v) при каждой итерации достаточно одного интегрирования. Начальные условия задаются на некоторой высоте r = r₀, где применимо приближение WKB. Использование матричного адмиттанса дает преимущество при численном расчете собственных значений радиального оператора.