
- •Министерство образования и науки российской федерации
- •Часть 1. Гамма-, бета- и пси-функции
- •390005, Рязань, ул. Гагарина, 59/1.
- •Предисловие
- •§ 1. Гамма-функция Эйлера (Эйлеров интеграл 2 рода)
- •Определение и простейшие свойства гамма-функции в комплексной области
- •Рассмотрим замкнутую область(см. Рис. 1.1).
- •Дальнейшие свойства гамма-функции
- •Примеры
- •Примеры на применение формулы
- •Другое интегральное представление гамма-функции и следствия из него
- •§ 2. Бета-функция Эйлера (Эйлеров интеграл 1 рода)
- •2.1. Определение и связь с гамма-функцией
- •2.2. Свойства бета–функции
- •2.3. Некоторые обозначения и символы
- •§ 3. Гамма-функция в вещественной области
- •Функциональная характеристика гамма-функции
- •3.2. График функции
- •3.3. График функции
- •4.2. Функция прии ее график
- •4.3. Дальнейшие свойства пси-функции
- •4.4. Вычисление преобразования Лапласа некоторых элементарных функций
- •4.4.1. Преобразование Лапласа функции
- •4.4.2. Преобразование Лапласа функции
4.4. Вычисление преобразования Лапласа некоторых элементарных функций
Вначале напомним
определение преобразования Лапласа.
Если функция
![]() обладает свойствами:
обладает свойствами:
 при
при ;
;на любом конечном интервале оси t функция
 имеет не более чем конечное число точек
разрыва 1 рода;
имеет не более чем конечное число точек
разрыва 1 рода; ,
то для нее в области
,
то для нее в области
 ,
где
,
где ,
а
,
а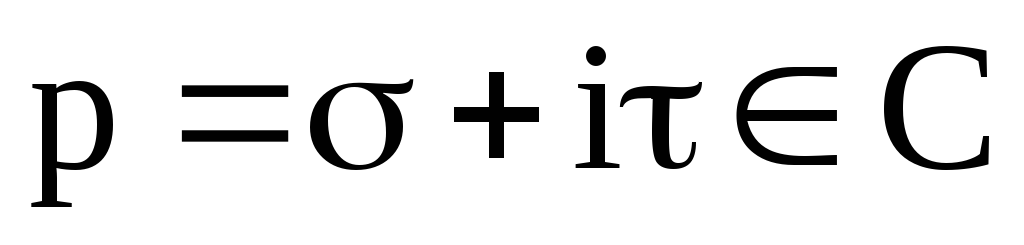 ,
определено преобразование Лапласа
,
определено преобразование Лапласа
![]() ,
,
4.4.1. Преобразование Лапласа функции
![]()
Имеем:
![]()
![]() и при
и при
![]()
![]() .
.
Этот интеграл
очень напоминает гамма-функцию Эйлера.
Но если в нем просто сделать замену
![]() то гамма-функция не получится, так как
интегрирование будет происходить не
по вещественной оси, а по лучу, проходящему
через точки 0 и
то гамма-функция не получится, так как
интегрирование будет происходить не
по вещественной оси, а по лучу, проходящему
через точки 0 и![]() (см. рис. 4.2).
(см. рис. 4.2).
П оэтому
надо действовать более аккуратно, взяв
вначале
оэтому
надо действовать более аккуратно, взяв
вначале![]() и воспользовавшись затем аналитическим
продолжением.
и воспользовавшись затем аналитическим
продолжением.
А именно, при
![]() рассмотрим функцию
рассмотрим функцию

![]() .
.
Таким образом,
![]() (в силу единственности аналитического
продолжения в область
(в силу единственности аналитического
продолжения в область![]() )
) - однозначная аналитическая функция в
области
- однозначная аналитическая функция в
области![]() .
.
Тем самым при
![]()
![]() .
.
В частности, при
![]()
![]()
при
 и т.д.
и т.д.
Следствие.
 .
.
4.4.2. Преобразование Лапласа функции
При
![]() и
и
![]() ,
(4.5)
,
(4.5)
причем этот интеграл
сходится при
![]() и сильно напоминает величину
и сильно напоминает величину![]() .
.
Однако, как и в
предыдущем примере, замену переменной
![]() в (5) делать нет смысла, так как интегрирование
будет происходить по лучу, проходящему
через точки 0 и р, а не по вещественной
оси. Поэтому вначале опять рассмотрим
случай вещественного
в (5) делать нет смысла, так как интегрирование
будет происходить по лучу, проходящему
через точки 0 и р, а не по вещественной
оси. Поэтому вначале опять рассмотрим
случай вещественного![]() :
:


Функция
![]() - аналитическая в области
- аналитическая в области![]() при
при![]()
![]() поэтому в силу единственности
аналитического продолжения при
поэтому в силу единственности
аналитического продолжения при![]()
![]() .
.
Таким образом,
![]()
Следствие.
![]() .
.
4.4.3.
Преобразование Лапласа функции
![]()
При
![]()
![]() и
и
![]() ,
причем этот интеграл сходится при
,
причем этот интеграл сходится при
![]() и сильно напоминает величину
и сильно напоминает величину![]() .
.
По аналогии с двумя
предыдущими примерами при
![]() имеем:
имеем:




Функция
 - аналитическая в области
- аналитическая в области![]() при
при![]()
 ,
поэтому в силу единственности
аналитического продолжения при
,
поэтому в силу единственности
аналитического продолжения при![]()
 .
.
Таким образом,
 .
.![]()
Следствие.

4.5. Примеры интегралов, выражающихся
через пси-функцию
![]()
![]() ;
;

![]() .
.
Библиографический список
Анго А. Математика для электро- и радиоинженеров. М.: Наука, 1965. 780 с.
Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Гипергеометрическая функция. Функции Лежандра. 2-е изд. М.: 1973. 296 с.
Бурбаки Н. Функции действительного переменного. Элементарная теория. М.: Наука, 1965. 424 с.
Вороной Г.Ф. Собрание сочинений. Т. 2. Киев.: АН УССР, 1952. 391 с.
Кратцер А., Франц В. Трансцендентные функции. М.: ИЛ. 1963. 466 с.
Кузнецов Д.С. Специальные функции. 2-е изд., испр. и доп. М.: Высшая Школа, 1964. 273 с.
Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. 5-е изд. М.: Наука, 1987. 688 с.
Люк Ю. Специальные математические функции и их аппроксимации. М.: Мир, 1980. 608 с.
Маркушевич А.И. Теория аналитических функций.
Т. 2. 2-е изд., испр. и доп. М.: Наука, 1968. 624 с.
Математический анализ. Функции, пределы, ряды, цепные дроби (Справочная математическая библиотека). М.: Физматгиз, 1961. 439 с.
Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган. М.: Наука, 1979. 832 с.
Уиттекер Э.Т., Ватсон Дж.Н. Курс современного анализа. Ч. 2. 2-е изд. М.: ГИФМЛ, 1963. 516 с.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 2. 7-е изд. М.: Наука, 1970. 800 с.
Шварц Л. Математические методы для физических наук. М.: Мир, 1965. 412 с.
Янке Е., Эмде Ф., Леш Ф. Специальные функции. Формулы, графики, таблицы. 3-е изд. М.: Наука, 1977. 344 с.
