
- •Министерство образования и науки российской федерации
- •Часть 1. Гамма-, бета- и пси-функции
- •390005, Рязань, ул. Гагарина, 59/1.
- •Предисловие
- •§ 1. Гамма-функция Эйлера (Эйлеров интеграл 2 рода)
- •Определение и простейшие свойства гамма-функции в комплексной области
- •Рассмотрим замкнутую область(см. Рис. 1.1).
- •Дальнейшие свойства гамма-функции
- •Примеры
- •Примеры на применение формулы
- •Другое интегральное представление гамма-функции и следствия из него
- •§ 2. Бета-функция Эйлера (Эйлеров интеграл 1 рода)
- •2.1. Определение и связь с гамма-функцией
- •2.2. Свойства бета–функции
- •2.3. Некоторые обозначения и символы
- •§ 3. Гамма-функция в вещественной области
- •Функциональная характеристика гамма-функции
- •3.2. График функции
- •3.3. График функции
- •4.2. Функция прии ее график
- •4.3. Дальнейшие свойства пси-функции
- •4.4. Вычисление преобразования Лапласа некоторых элементарных функций
- •4.4.1. Преобразование Лапласа функции
- •4.4.2. Преобразование Лапласа функции
2.3. Некоторые обозначения и символы
 .
.
В этих обозначениях
![]()
В § 1 было доказано, что
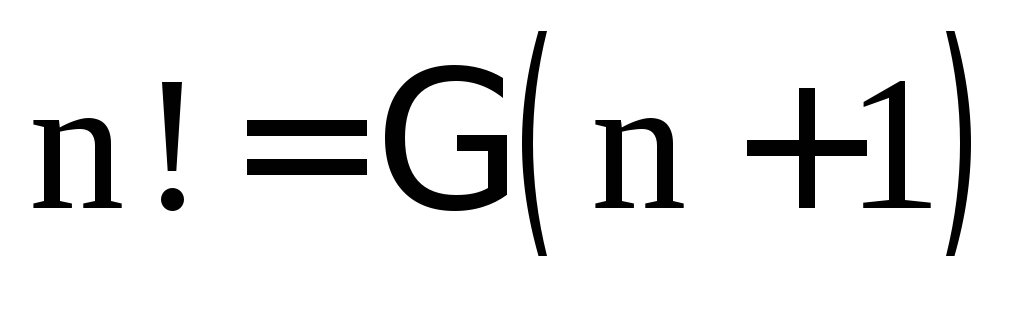 .
Иногда наряду с гамма-функцией
рассматривают близкую к ней
.
Иногда наряду с гамма-функцией
рассматривают близкую к ней
![]() .
.
Так как при этом
![]() ,
то именно
,
то именно![]() -функцию
естественно считать продолжением
факториала в комплексную область.
-функцию
естественно считать продолжением
факториала в комплексную область.
![]() можно определить
величину
можно определить
величину
![]() ,
которую естественно считать продолжением
биномиальных коэффициентов в комплексную
область.
,
которую естественно считать продолжением
биномиальных коэффициентов в комплексную
область.
Для
 символ Похгаммера
символ Похгаммера определяется следующим образом:
определяется следующим образом: ;
при
;
при
![]() .
.
Последняя формула,
во-первых, позволяет для всех
![]() записать символ Похгаммера единообразно
и, во-вторых, естественным образом
продолжить его в комплексную область
формулой
записать символ Похгаммера единообразно
и, во-вторых, естественным образом
продолжить его в комплексную область
формулой
![]() .
.
Символ Похгаммера позволяет компактно записывать некоторые формулы, например, бином Ньютона:
![]()
![]()
![]() .
.
§ 3. Гамма-функция в вещественной области
Функциональная характеристика гамма-функции
Многие функции однозначно определяются своими характерными свойствами. Например, хорошо известны функциональные уравнения, однозначно определяющие элементарные функции.
Теорема 1.
Если
![]() и
и
![]() то
то
![]() .
.
Теорема 2.
Если![]() ,
,![]() и
и
![]() то
то
![]()
Теорема 3.
Если![]() и
и
![]() то
то
![]() .
.
Теорема 4.
Если![]() ,
,![]() и
и
![]() то
то
![]() .
.
Теорема 5.
Если![]() ,
,![]() и
и
![]() то
то
![]() или
или
![]() .
.
Возникает естественный вопрос: нельзя ли и гамма-функцию однозначно определить какими-либо ее свойствами?
Мы знаем, что
функция
![]() непрерывна вместе со своей производной
для положительных значений аргумента.
Кроме того, она удовлетворяет следующим
функциональным уравнениям:
непрерывна вместе со своей производной
для положительных значений аргумента.
Кроме того, она удовлетворяет следующим
функциональным уравнениям:
![]() ,
(3.1)
,
(3.1)
![]() ,
(3.2)
,
(3.2)
![]() .
(3)
.
(3)
Утверждается, что
эти свойства в совокупности вполне
характеризуют функцию
![]() (так что каждая функция, обладающая
этими свойствами, тождественна с
(так что каждая функция, обладающая
этими свойствами, тождественна с![]() ).
).
Заметим, что одних
свойств (1) и (2) для этого недостаточно,
так как, наряду с
![]() ,
ими обладает и функция
,
ими обладает и функция
![]() (при
(при
![]() ).
).
Точно так же недостаточно и свойств (2) и (3), ибо они принадлежат и функции
![]() (при
(при
![]() ).
).
Наконец, свойства
(1) и (3) явно оставляют произвольными
значения функции
![]() для
для![]() .
Иначе обстоит дело, если налицо все три
свойства. Впрочем, свойство (3) можно
заменить более слабым требованием,
чтобы функция
.
Иначе обстоит дело, если налицо все три
свойства. Впрочем, свойство (3) можно
заменить более слабым требованием,
чтобы функция![]() при
при![]() не обращалась в ноль, что как раз и
вытекает из (3). А именно, справедливо
следующее утверждение.
не обращалась в ноль, что как раз и
вытекает из (3). А именно, справедливо
следующее утверждение.
Теорема
3.1. Если
функция
![]() ,
отлична от нуля и удовлетворяет
соотношениям (1) и (2):
,
отлична от нуля и удовлетворяет
соотношениям (1) и (2):
![]() и
и
![]()
то
![]() .
.
Можно дать более простую характеристику гамма-функции, используя лишь одно функциональное уравнение (1), но налагая на функцию еще и требование логарифмической выпуклости.
Напомним, что
положительная функция
![]() ,
заданная на интервале
,
заданная на интервале![]() ,
называется логарифмически выпуклой на
этом промежутке, если ее логарифм
,
называется логарифмически выпуклой на
этом промежутке, если ее логарифм![]() оказывается выпуклой функцией.
оказывается выпуклой функцией.
Так как
![]() ,
то из логарифмической выпуклости функции
,
то из логарифмической выпуклости функции![]() вытекает ее выпуклость; обратное
заключение, вообще говоря, неверно.
Таким образом, логарифмически выпуклые
функции составляют лишь часть всего
класса выпуклых функций.
вытекает ее выпуклость; обратное
заключение, вообще говоря, неверно.
Таким образом, логарифмически выпуклые
функции составляют лишь часть всего
класса выпуклых функций.
Для функции
![]() имеем:
имеем:
![]()
![]() .
.
Докажем, что при
![]() справедливо неравенство
справедливо неравенство
![]()
![]() .
(3.4)
.
(3.4)
Действительно,
при
![]() имеем:
имеем:
![]() .
Отсюда
.
Отсюда
![]()
![]()
и (4) превращается в

![]() .
(3.5)
.
(3.5)
Возьмем в неравенстве Коши-Буняковского
 (3.6)
(3.6)
![]()
![]() .
.
Тогда
![]()
и (5) вытекает из
(6) при
![]() и
и![]() .
.
Тем самым для
функции
![]() при
при![]() справедливо неравенство
справедливо неравенство![]()
![]() ,
т.е.
,
т.е.![]() выпукла вниз и
выпукла вниз и![]() логарифмически выпукла.
логарифмически выпукла.
Вот этим-то
свойством, совместно с уравнением (1),
функция
![]() и определяется с точностью до постоянного
множителя.
и определяется с точностью до постоянного
множителя.
Теорема 3.2. Если
![]() при
при![]() и
и
I.
![]() ,
,
II.
![]() логарифмически выпукла,
логарифмически выпукла,
III.
![]() ,
то
,
то![]() .
.
