3. Примеры

Приведем далее несколько примеров на применение полученных формул при вычислении интегралов.

Пример 1.1

,

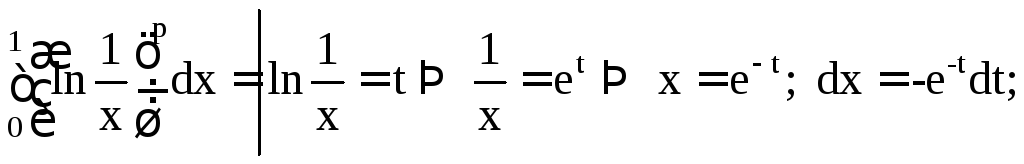
причем последний интеграл, а с ним и исходный, сходятся при

Пример 1.2.

.

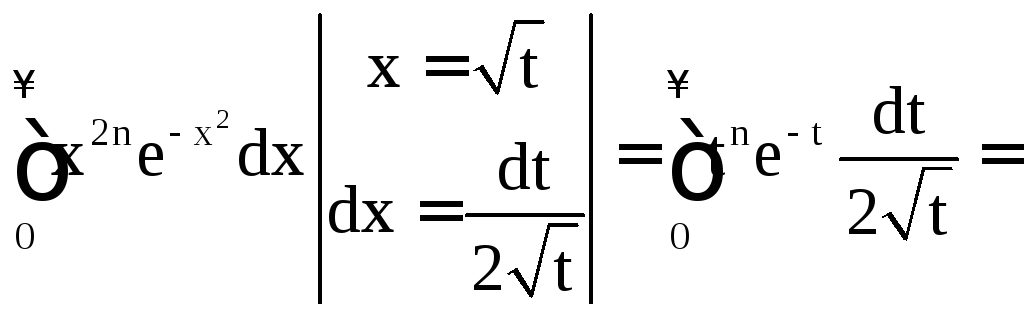
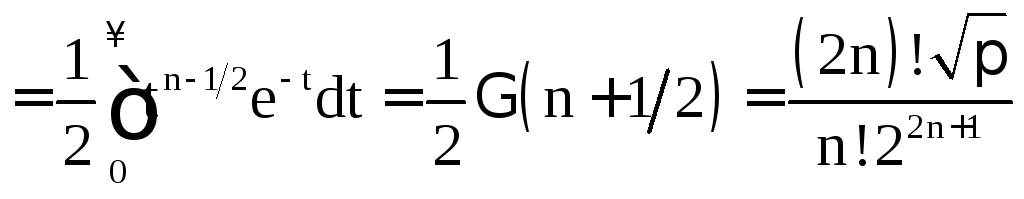Пример 1.3. .

Пример 1.4. =

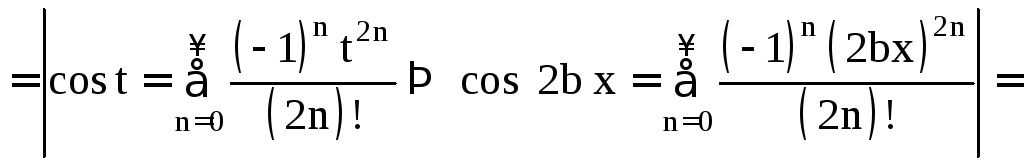
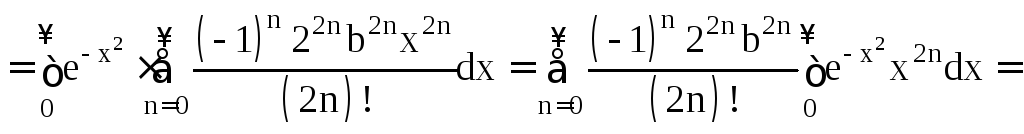
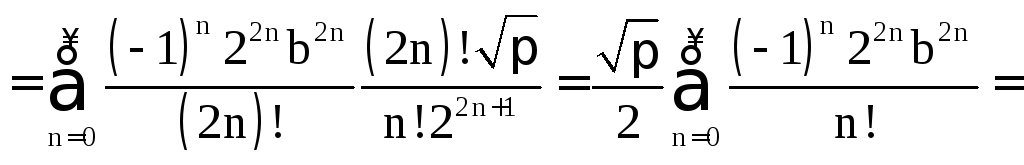
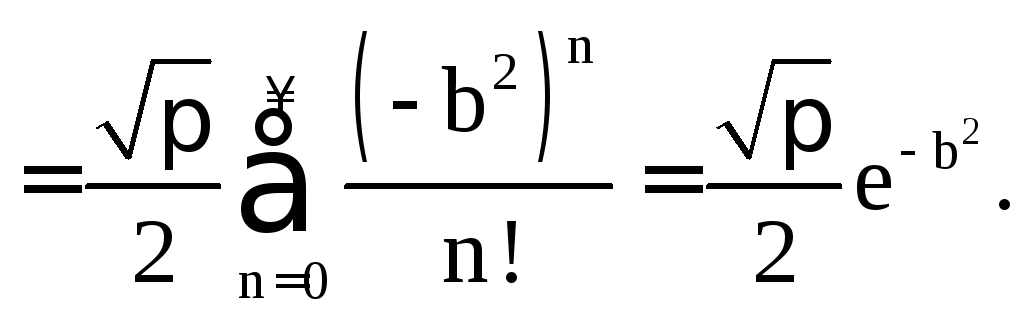
Примеры на применение формулы

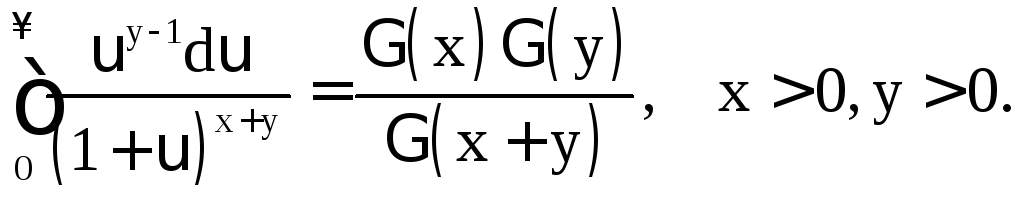
Пример 1.5.

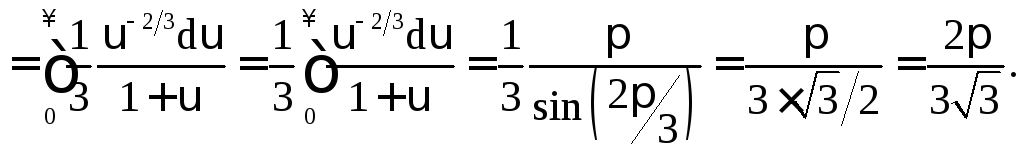
Пример 1.6. .

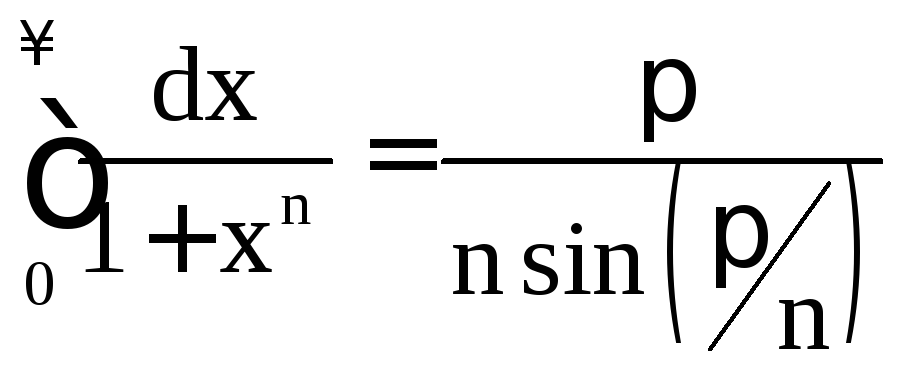Пример 1.7. .

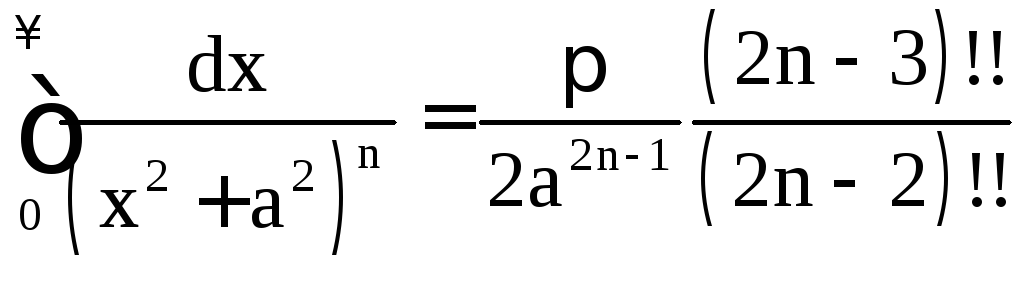
Пример 1.8

.

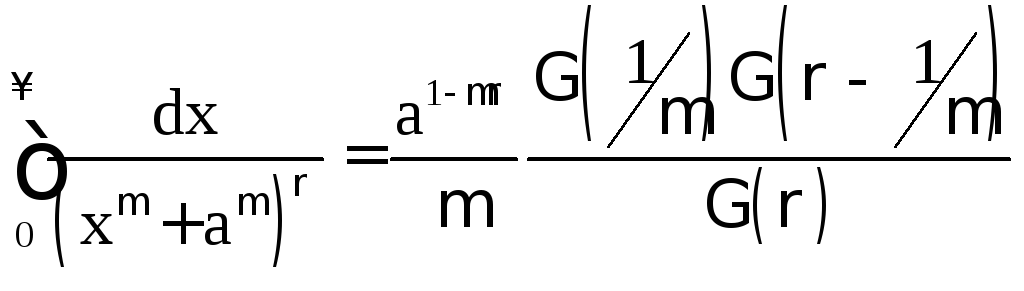
Пример 1.9.

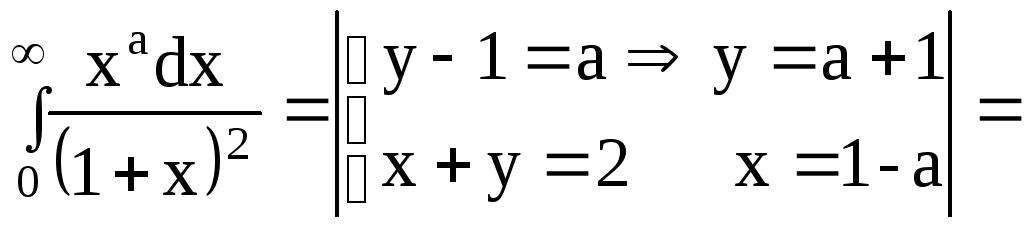
Интеграл сходится, если

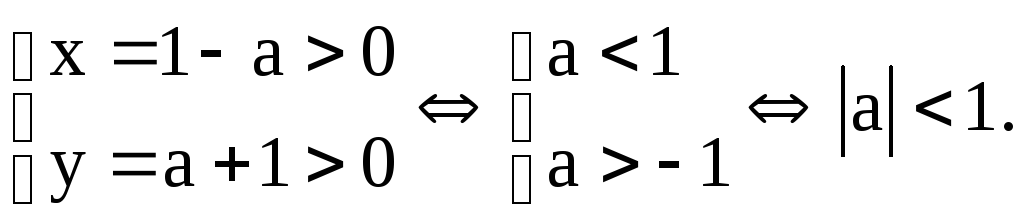
Пример 1.10. .

Решение. Рассмотрим интеграл

.

Вычислим

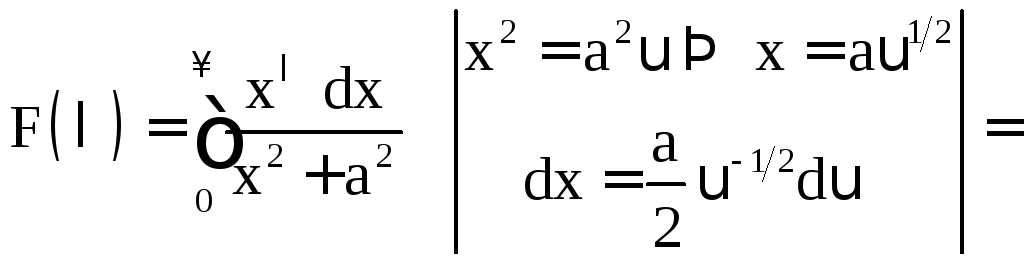
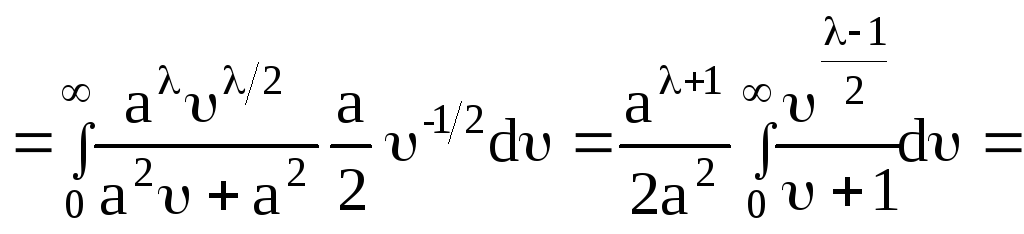
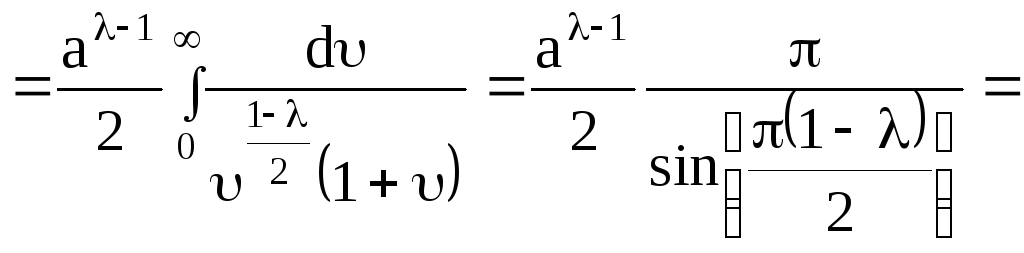
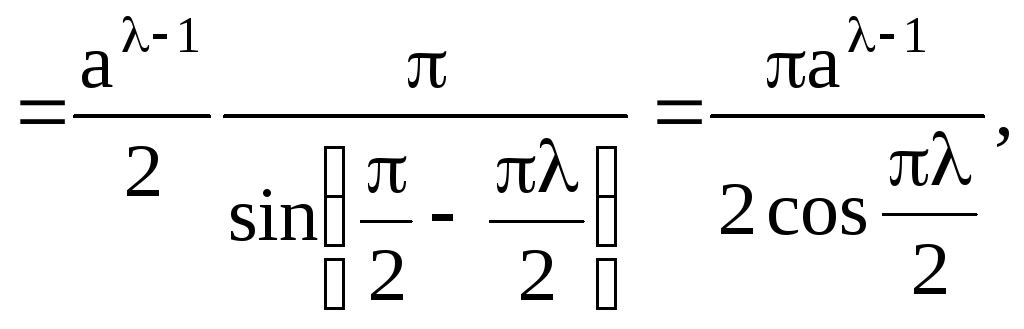
причем интеграл сходится тогда и только тогда, когда

Таким образом, при

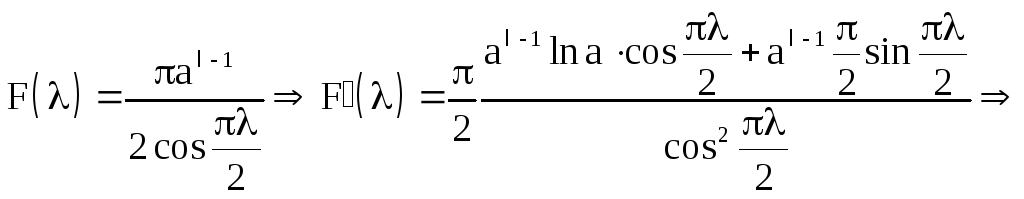
Пример 1.11. , причем величинанайдена в предыдущем примере. Следовательно,

.

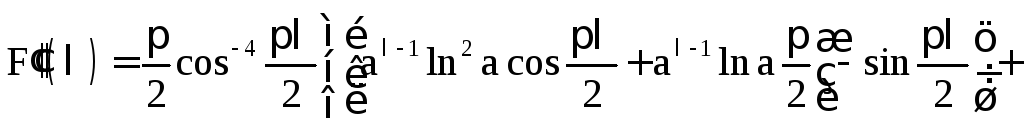
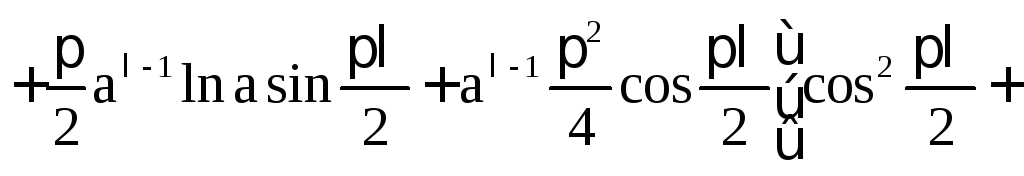
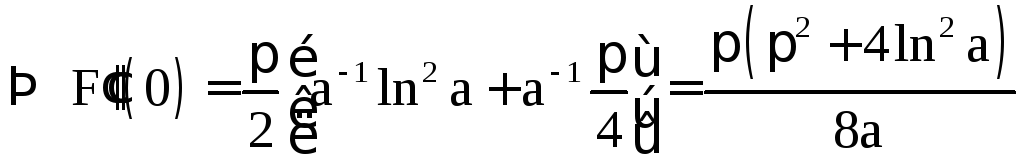Пример 1.12. .

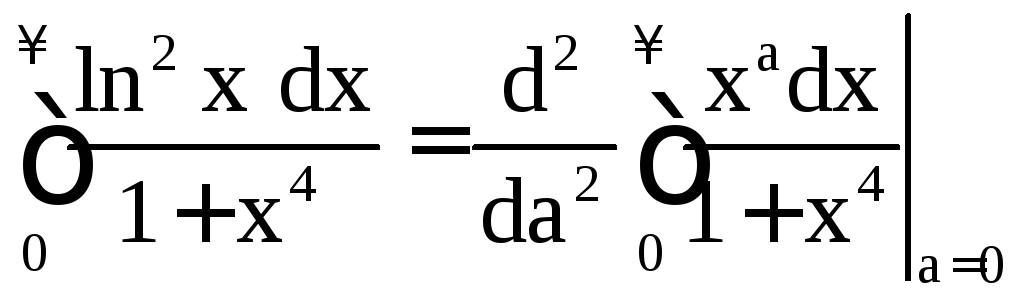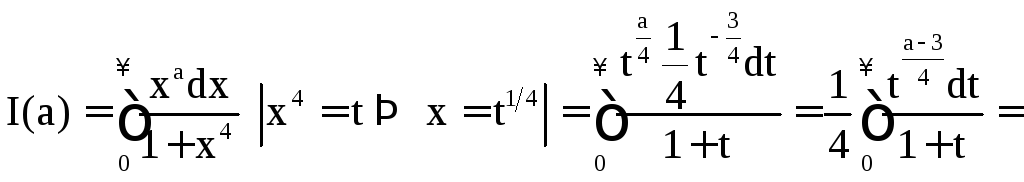
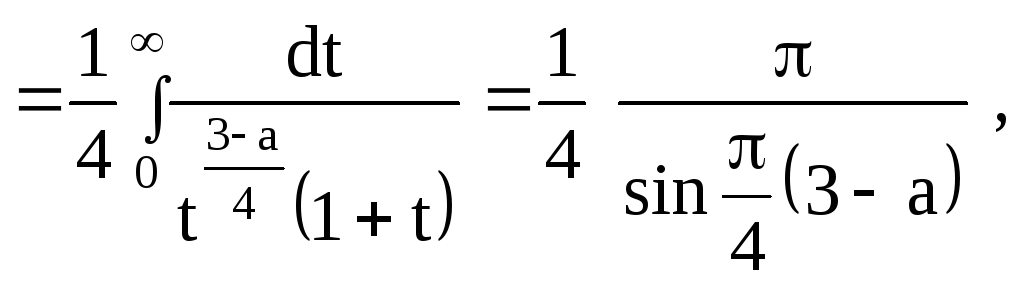
причем все интегралы сходятся .

Таким образом, при

;

.

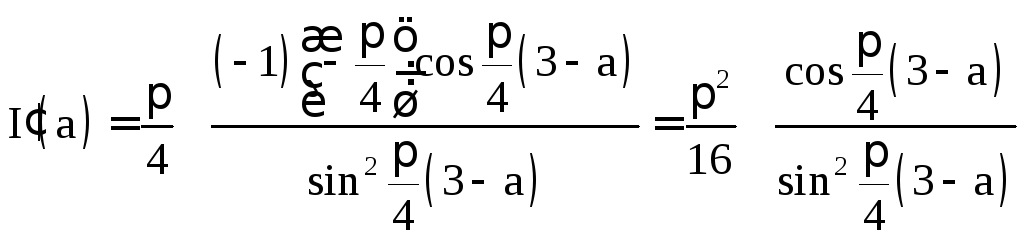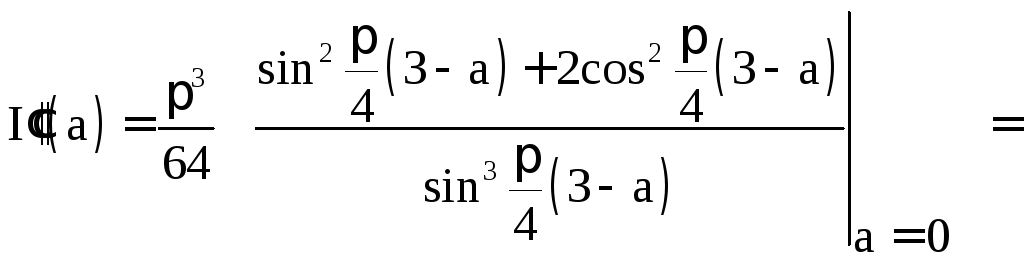
Пример 1.13.

.

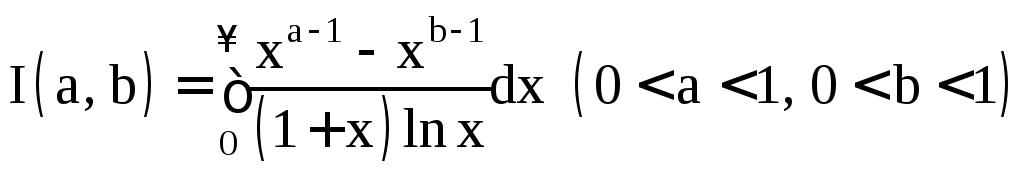Решение.

. Отсюда

Но , т.е. при

.

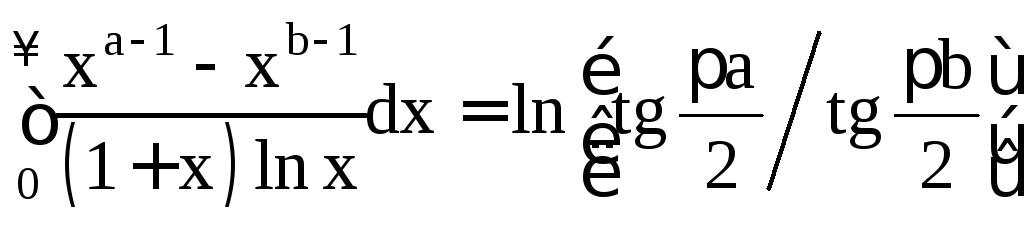При отсюда получается любопытный интеграл

.

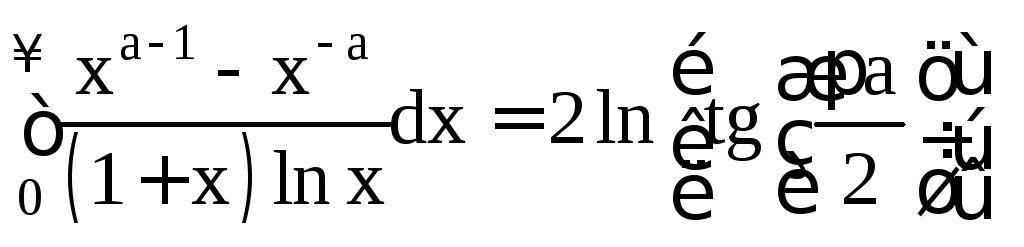
Пример 1.14.

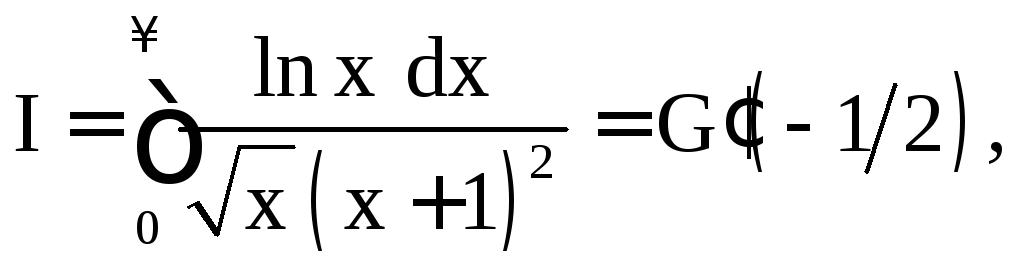
где 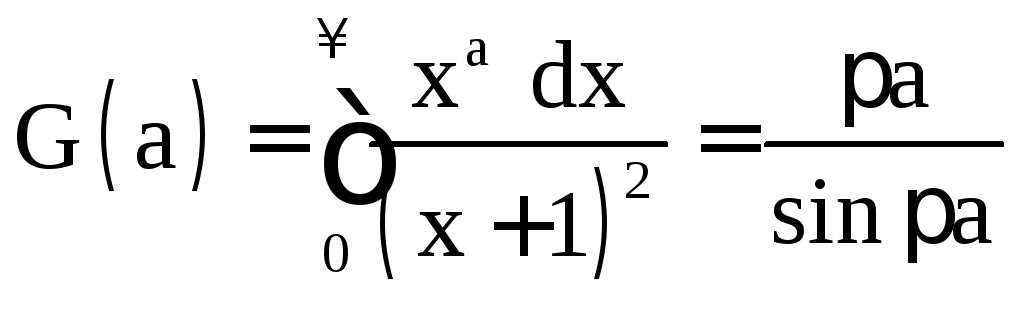(см. пример 1.9). Отсюда

Пример 1.15. Докажем, что при

1. При сделаем замену переменной

;

причем интеграл сходится .

2. При 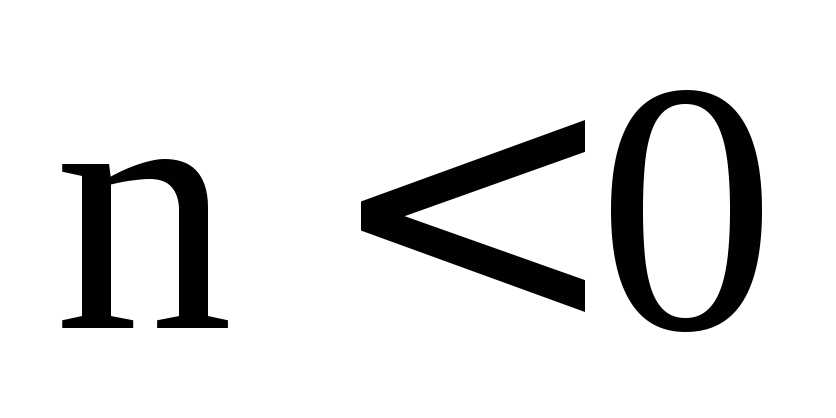проходит та же замена переменной,

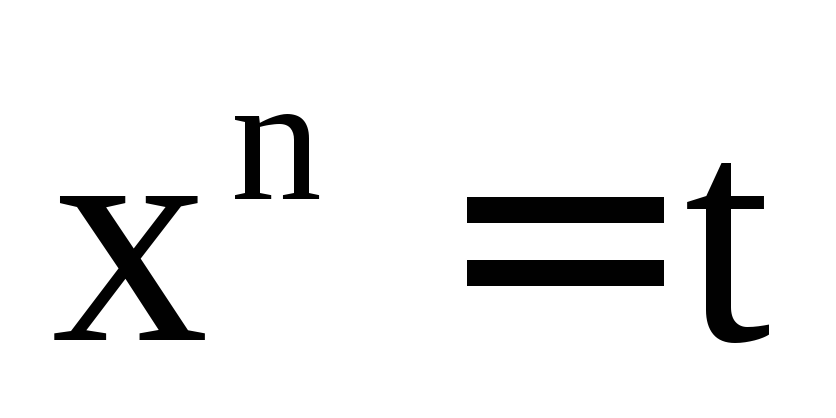но теперь пределы интегрирования меняются местами:

причем для сходимости интегралов по-прежнему должно выполняться условие .

Пример 1.16. .

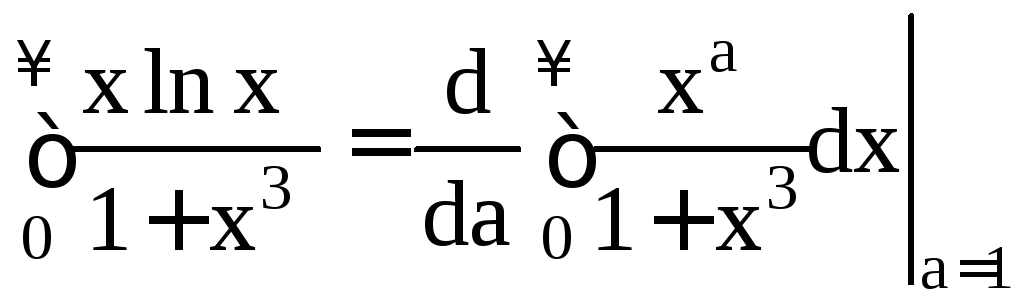Обозначим

,

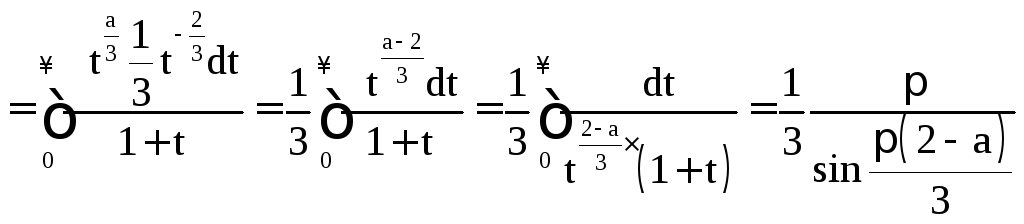причем для сходимости интегралов должно выполняться условие .

При этих значениях a

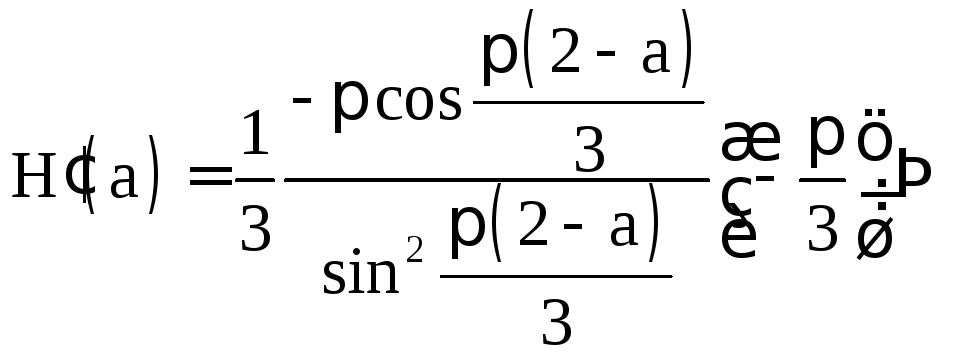
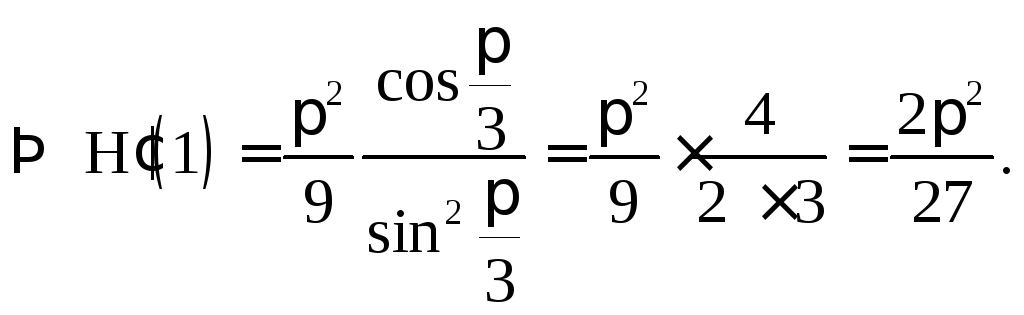
Пример 1.17. Рассмотрим интеграл . Этот интеграл сходится, так как в окрестности нуляа интегралсходится.

Сделаем в замену переменной

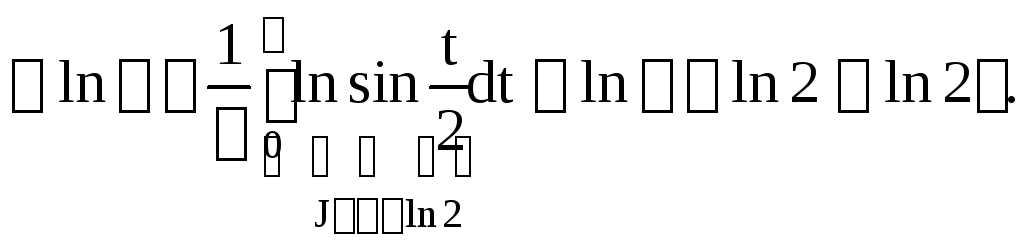
Таким образом,

Пример 1.18. Раабе рассмотрел интеграл

Так как то

Так как сохраняет непрерывность прито

.

С другой стороны,

и .

Пример 1.19. Рассмотрим интеграл

Сделаем в нем замену переменной

.

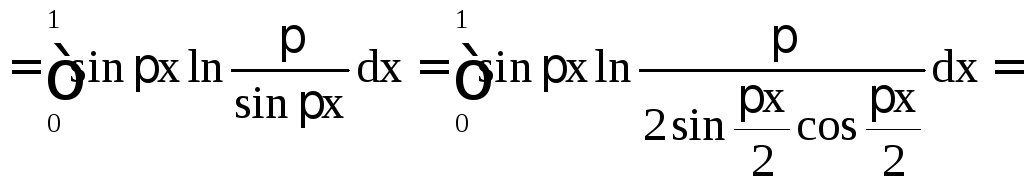
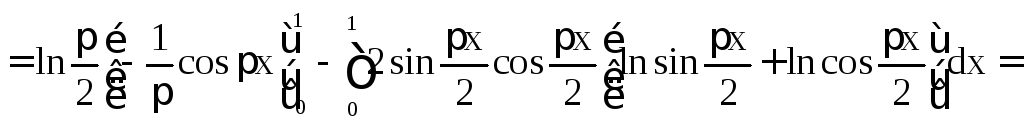
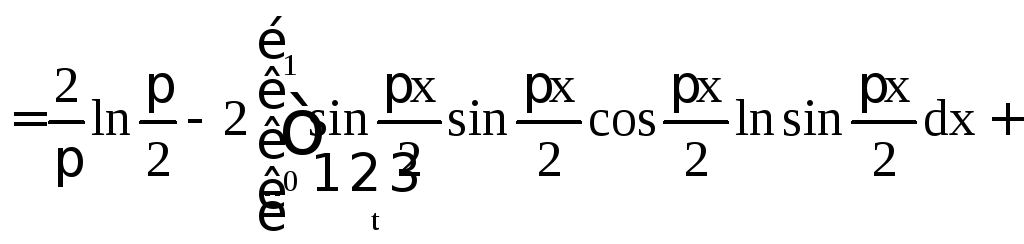
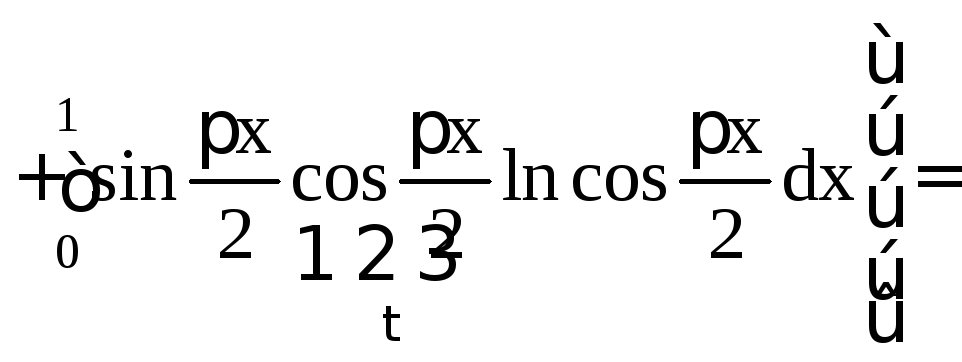
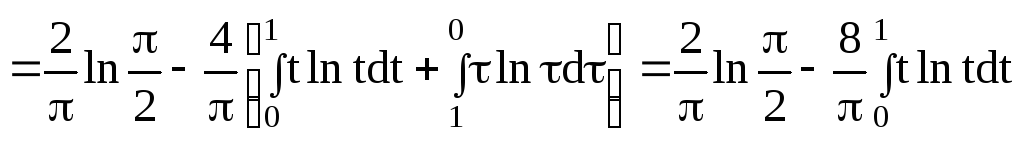Последний интеграл вычислим «по частям»:

.

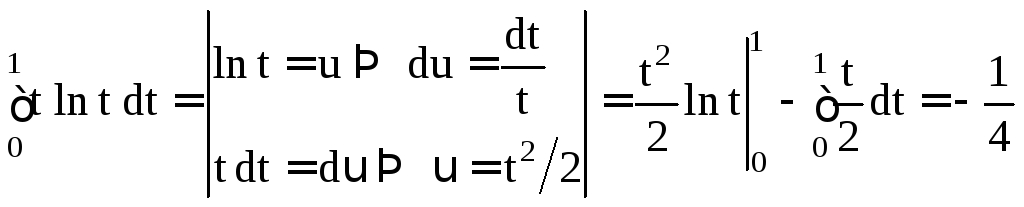Тем самым .

4. Другое интегральное представление гамма-функции и следствия из него

1.4.1. Докажем, что при имеет место формула

(1.7)

Д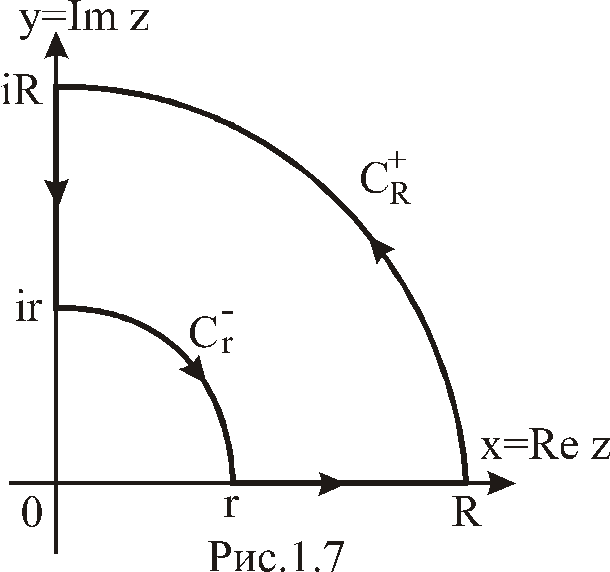оказательство.

Рассмотрим замкнутый контур , изображенный на рис. 1.7. Так как при фиксированномфункция- аналитическая, то согласно теореме Коши.

С другой стороны,

(1.8)

.

Оценим подынтегральную функцию в (8) по модулю:

.

Пусть фиксировано. Тогда при

, если . Следовательно, согласно лемме Жорданапри.

Далее, 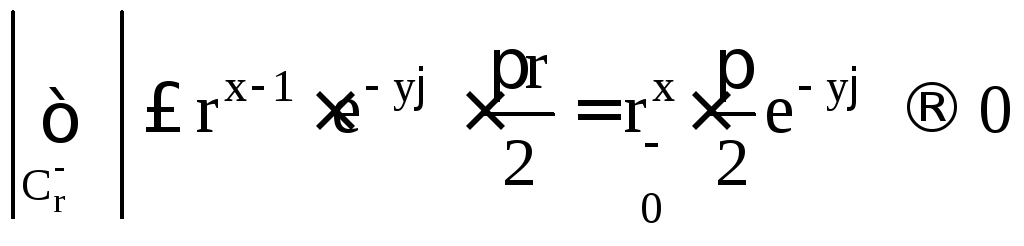при,

если . Остается рассмотреть интеграл. Сделаем в нем замену переменной,. Получим:

.

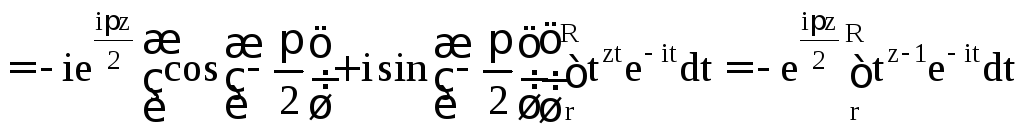Устремляя в (8) и, получаем при

, ч.т.д.

1.4.2. Докажем что при

, (1.9)

. (1.10)

Доказательство. Взяв в формуле (7) и отделяя вещественную и мнимую части, получаем:

Формулы (9) и (10) вытекают отсюда с помощью аналитического продолжения.

Интегралы более общего вида

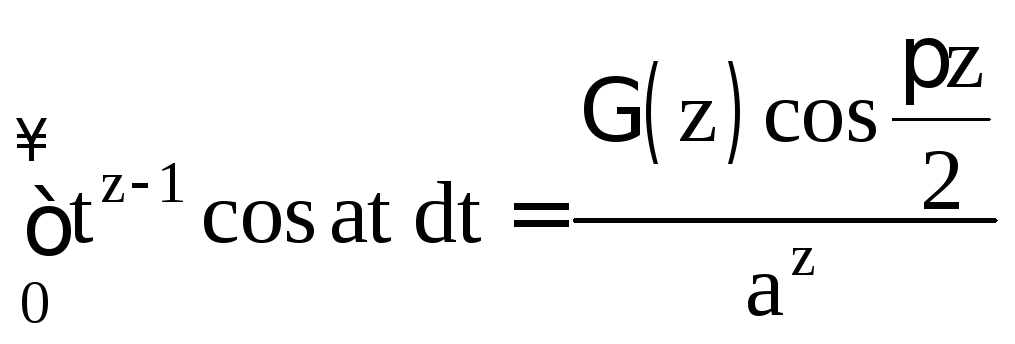
(1.11)

и

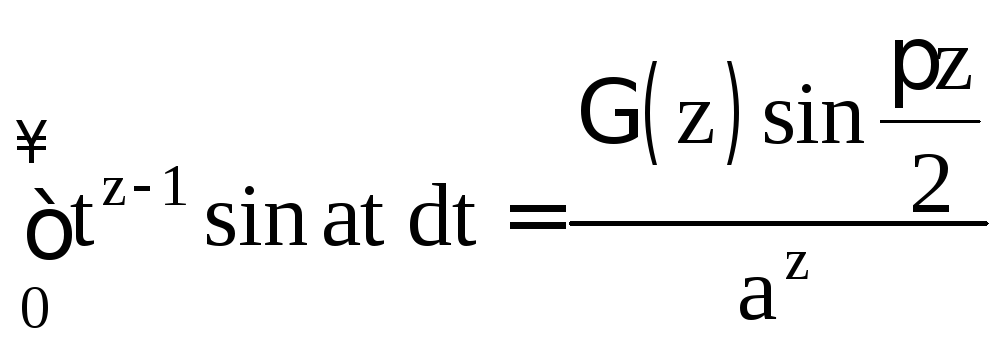
(1.12)

вытекают из (3) и (4) соответственно при с помощью замены переменнойи аналитического продолжения.

1.4.3. Докажем, что

(1.13)

и

(1.14)

Решение. Имеем:

.

Далее выполним в формуле (7) замену переменной ;

.

В частности, при

,

откуда, отделяя вещественную и мнимую части, получаем интегралы (13) и (14).

1.4.4. Докажем, что при

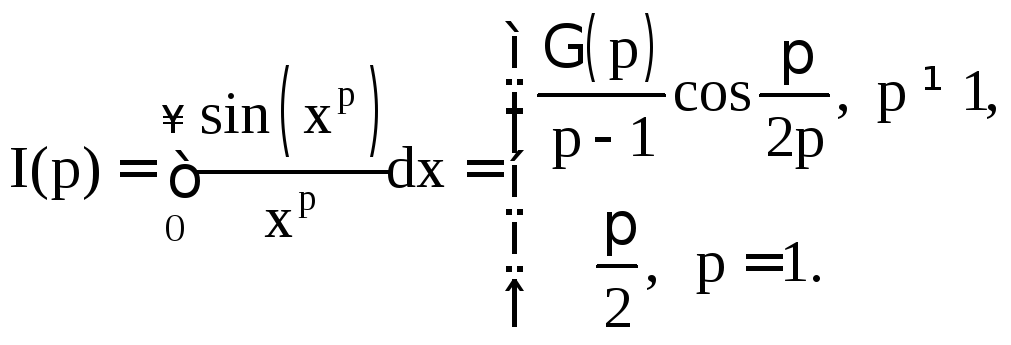
Решение. Первым делом выполним в интеграле замену переменной.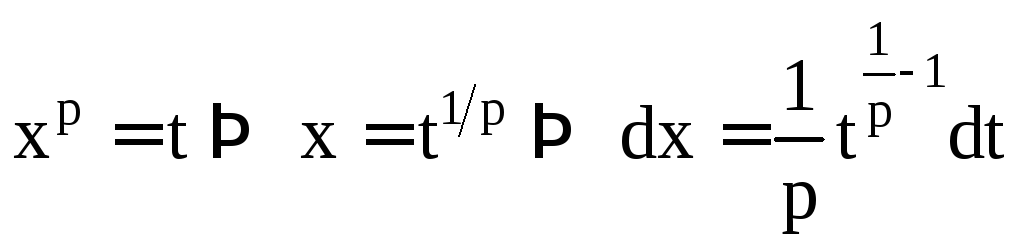

Получим: .

Этот интеграл сходится в нуле при ;

сходится на бесконечности при .

Тем самым при .

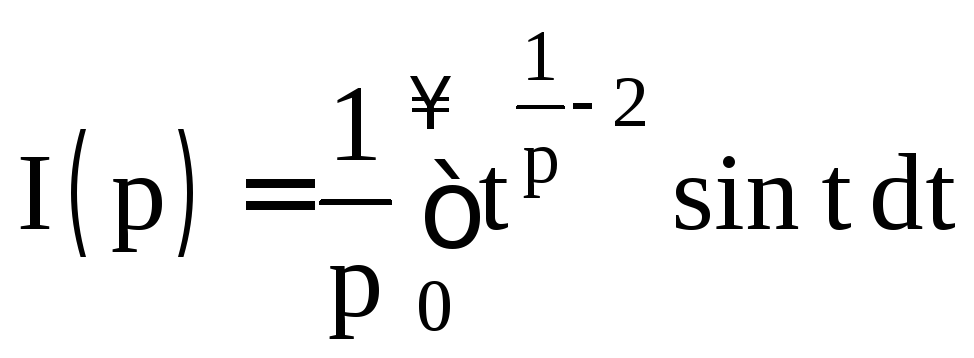Далее воспользуемся формулой (7) .

Взяв здесь , приполучаем

.

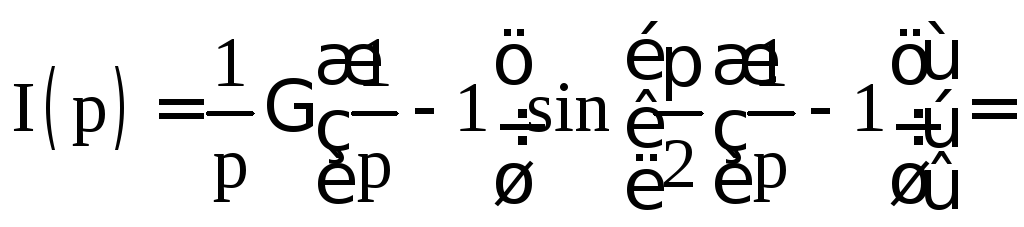
При

.
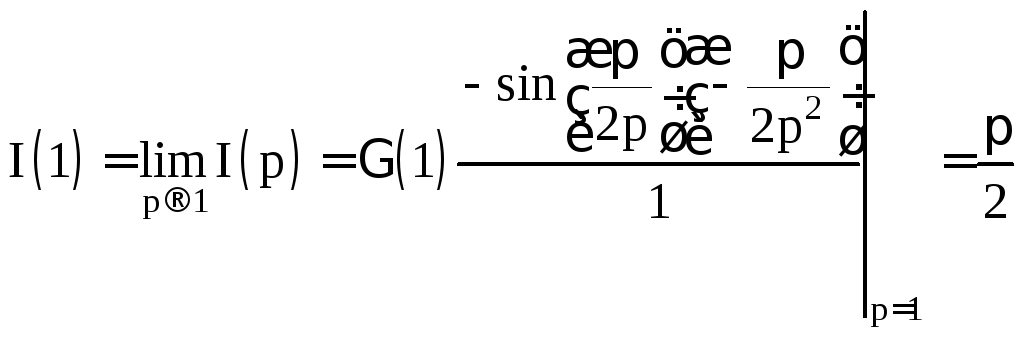