МАРКЕТИНГ-ПР.ЗАН.ОЦЕНКА КОНКУРЕНЦИИ

ИЗУЧЕНИЕ КОНКУРЕНЦИИ НА РЫНКЕ МЕТОДОМ КЛАСТЕРНОГО АНАЛИЗА

1.Алгоритм кластерного анализа

Кластерный анализ – это совокупность методов классификации многомерных наблюдений или объектов, основанных на определении понятия расстояния между объектами с последующим выделением из этих объектов групп, “сгустков” наблюдений (кластеров, таксонов). При этом не требуется априорной информации о распределении генеральной совокупности.

Выбор конкретного метода кластерного анализа зависит от цели классификации и в настоящее время весьма разнообразен, затрагивая целые математико-статистические разделы, начиная от традиционного – исследования операций и заканчивая, к примеру, многомерным шкалированием.

Кластерный анализ используется при исследовании структуры совокупностей менеджерских, социально-экономических, маркетинговых, коммерческих показателей или объектов: предприятий, фирм, корпораций, регионов, территорий, социологических анкет, коллективов, популяций и сообществ и т.д.

От матрицы исходных данных:

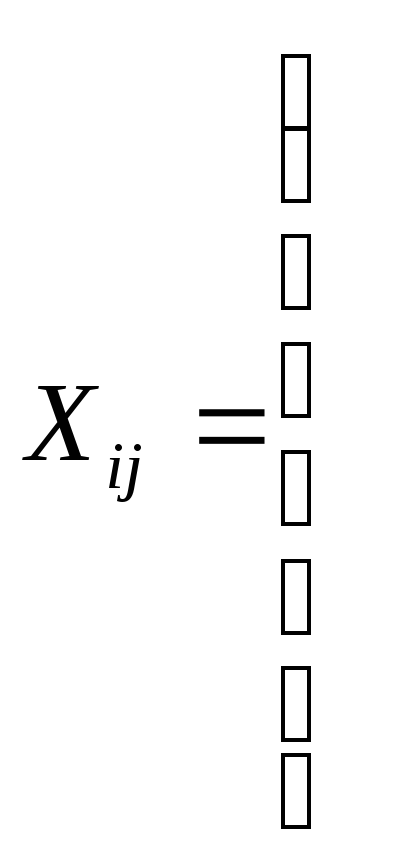
переходим к матрице нормированных значений с элементами

где - номер показателя (столбцы), номер наблюдателя (строки);

;

Таким образом, получим матрицу :

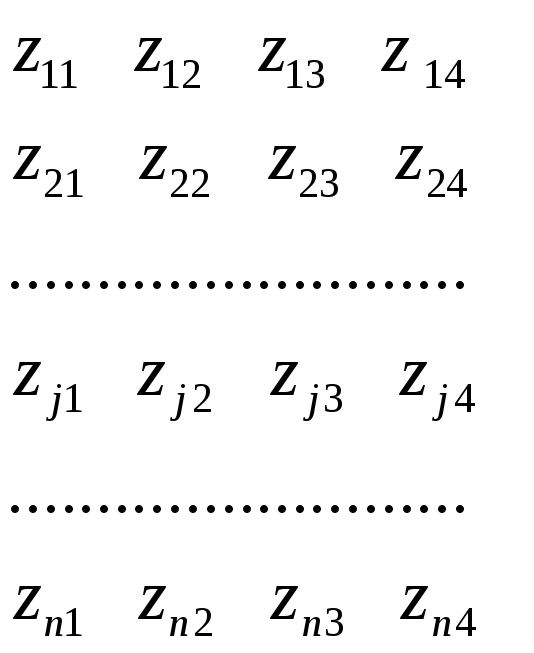
В качестве «расстояния» между наблюдениями и используют (чаще всего, и даже, в основном) «взвешенное» евклидовое расстояние, определяемое по формуле:

, где - вес показателя; .

Если для всех , то получаем обычное евклидовое расстояние:

,

Полученные расчетом для каждой ячейке значения удобно представить в виде матрицы расстояний:

; .

Так как матрица симметрическая, т.е. , то достаточно ограничиться записью наддиагональных элементов матрицы.

Используя матрицу расстояний, можно реализовать подобную иерархическую «цементирующую» процедуру кластерного анализа. Расстояния между кластерами определяют по принципу «ближнего соседа» или «дальнего соседа». В первом случае за расстояние между ближайшими элементами этих кластеров, а во втором – между удаленными друг от друга.

Принцип работы иерархических «цементирующих» процедур состоит в последовательном объединении групп элементов сначала самых близких, а затем все более отдаленных друг от друга.

На каждом шаге алгоритма каждое наблюдение () рассматривается как отдельный кластер. В дальнейшем на каждом шаге работы алгоритма происходит объединение двух самых близких кластеров, и вновь строится матрица расстояний, размерность которой снижается на единицу.

Результаты итеративных процедур объединения строк и столбцов кластеров позволяет построить дендрограмму взаимодействия с учетом минимальных, а главное относительно пропорциональных условных «расстояний».

1 2 3 4 5

Дендрограмма, характеризующая кластер условных «расстояний» примера, объединенного по выявленным ( ) минимально возможным «расстояниям».

2. Практический расчет оценки конкуренции на рынке

Задание 1: Выявить уровень конкуренции Северо-западного региона российского рынка электротехнической промышленности, где одно из пяти предприятий относится к Калининградскому региону (производство кабельной продукции). Каждое предприятие характеризуется следующими экономическими показателями: - прибыль от реализации (млн. руб.);

- удельный вес высококачественной продукции (%);

- выработка товарной продукции на одного работника ППП (тыс. руб.);

- среднегодовая стоимость основных производственных фондов (млн. руб.).

Данные сведены в табл. 1.1.

Таблица 1.1 Значения основных экономических показателей предприятий электротехнической промышленности Северо-Западного региона России

№ пред- приятия пр	Показатели оценки конкурентоспособности предприятия
	-	-
1	3,338	78,46	5,013	7,312
2	1,909	50,83	3,423	17,785
3	6,653	26,12	3,314	21,544
4	2,105	72,11	2,534	8,125
5	6,178	13,10	1,863	1,780

Таблица 1.1 является исходной матрицей двумерной классификации. Для устранения различия в единицах измерения показателей нормируем их. В результате нормировки получаем приведенную матрицу исходных данных:

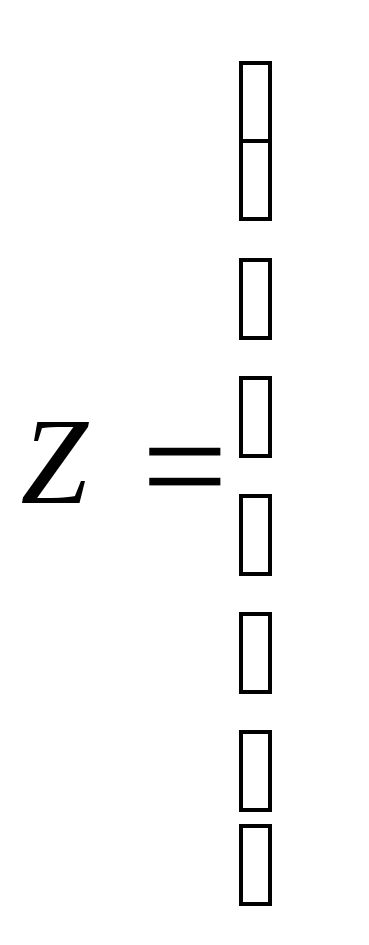
-0,34776501	1,1996448	1,688891	-0,55050379
-1,0591251	0,1026702	0,1833199	0,89186241
1,3024511	-0,8783738	0,0801078	1,4095607
-0,96155583	0,9475352	-0,6584743	-0,43853551
1,0699948	-1,3714763	-1,2938443	-1,3123838

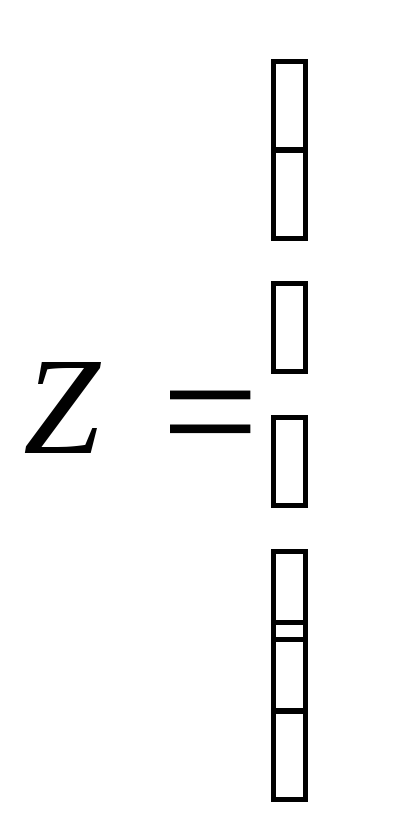
а также средние значения показателей и их средние квадратические отклонения:

В качестве расстояния между объектами принято евклидово расстояние, причем “веса” заданы (путем привлечения экспертных оценок) пропорционально степени важности экономического показателя, например: .

Используя формулу расчета эвклидовых расстояний с учетом “весовых” коэффициентов, рассчитываем матрицу расстояний , которая (в силу симметричности) представлена как треугольная.

0	1,159804	1,9283079	1,1311047	2,2980731
	0	1,6262618	0,77977305	1,8968315
		0	1,9581917	1,1126867
			0	1,9881173
				0

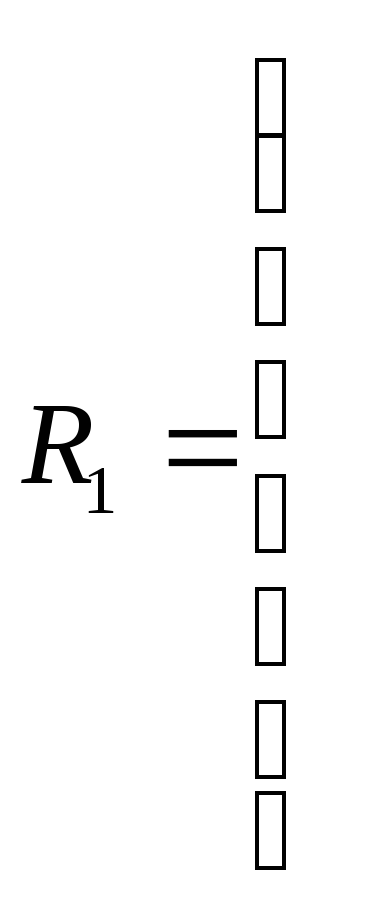
Из матрицы следует, что объекты 2 и 4 наиболее близки () и поэтому возможно их объединение в один кластер, исходя из условия минимизации “расстояния”. После объединения имеем четыре кластера:

Номера кластера	1	2	3	4
Состав К кластера	(1)	( (2,4)	(3)	(5)

Расстояние между кластерами будем находить по принципу “ближнего соседа”. За расстоянием между кластерами 1 и (2,4) выбираем минимальное из расстояний и . Аналогично находим расстояния между кластерами 2, 5 и (2,4), которые соответственно равны: и . Расстояние между остальными кластерами можно считать не изменяющимися. Таким образом, получаем матрицу расстояний

0	1,1311047	1,9283079	2,2980731
	0	1,6262618	1,8968315
		0	1,1126867
			0

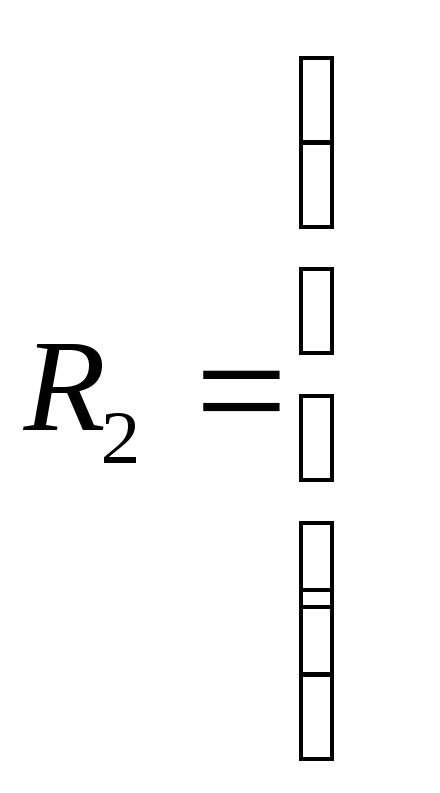
Из матрицы следует, что кластеры 3 и 5 наиболее близки () и поэтому объединяются в новый кластер (3,5). После объединения будем иметь три кластера 1, (2,4) и (3,5). Расстояния между новым кластером (3,5) и кластерами 1 и (2,4) соответственно равны: ( меньше ) и . Поэтому матрица расстояний принимает следующий вид:

0	1,1311047	1,9283079
	0	1,6262618
		0

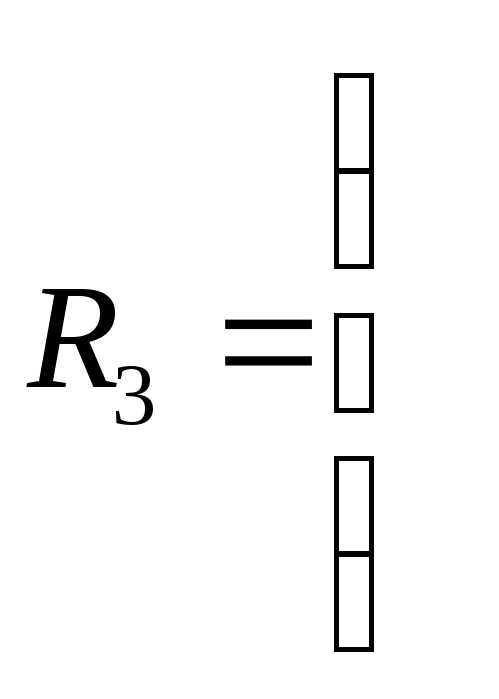
Из этой матрицы следует, что кластеры 1 и (2,4) объединяются в новый кластер (1+2,4), так как расстояние между ними минимально и равно .

Тогда получим матрицу расстояний:

0	1,6262618
	0

Таким образом, на расстоянии два кластера (1,2,4) и (3,5) объединяются в один.

Результаты иерархической классификации наблюдений представлены на рис. 1 в виде дендрограммы, где по оси ординат приводятся относительные “расстояния” при объединении показателей работы предприятий с учетом “весовых” вкладов каждого параметра. Поэтому расстояния между исходными кластерами-предприятиями можно расценивать как конкурирующие факторы или факторы, необходимые для объединения в совместной деятельности с выгодой для себя и в ущерб остальным. Возможны и другие интерпретации, уровень которых зависит от квалификации и знания дела менеджером.

Задание 2 Оценка уровня конкуренции методом кластерного анализа

Определить уровень конкурентоспособности ООО «СТК-Балт».

Исходные данные: В таблице 1.2 представлены строительные предприятия жилья Калининградского региона по следующим экономическим показателям:

1 – Объем производства (млн.руб.)

2- Цена за 1 кв.метр (руб.)

3- Маржинальная прибыль (млн. руб.)

4- Коэффициент фондоотдачи основных средств

5- Коэффициент рентабельности производства

6- Коэффициент оборачиваемости активов

Таблица 1.2 Исходные данные дл анализа конкуренции предприятий на рынке строительства жилья

Предприятия	1- объем произв	2 - цена	3 – маржин прибыль	4 – коэффиц фондоотд	5 – коэффиц рентаб	6 – коэффиц. оборач. актив
Макрострой	5120	37	4890	1,35	0,15	0,29
ЖБИ-1	4900	40	4690	1,27	0,15	0,19
СТК-Балт	5337	38	4373	1,36	0,17	0,27
Вента	4700	40	4520	1,2	0,1	0,18
НовоБалтИнвест	5070	45	4870	1,2	0,13	0,2
Ср. значение	5020,4	40	4668,60	1,276	0,14	0,226
Ср. квадрат. отклонение	214,31	2,75	199,75	0,07	0,02	0,044

1. Матрица нормированных значений. Zij = (xij – xср.)/sij

0,44	-1,09	1,11	1,07	0,42	1,42
-0,59	0,00	0,11	-0,09	0,42	-0,80
1,45	-0,73	-1,48	1,21	1,27	0,98
-1,52	0,00	-0,74	-1,09	-1,69	-1,02
0,21	1,81	1,01	-1,09	-0,42	-0,58

разница12	1,03	-1,09	1,00	1,15	0,00	2,22
разница13	-1,01	-0,36	2,59	-0,14	-0,85	0,44
разница14	1,96	-1,09	1,85	2,16	2,11	2,45
разница15	0,23	-2,90	0,10	2,16	0,85	2,00
разница23	-2,04	0,73	1,59	-1,30	-0,85	-1,78
разница24	0,93	0,00	0,85	1,01	2,11	0,22
разница25	-0,79	-1,81	-0,90	1,01	0,85	-0,22
разница34	2,97	-0,73	-0,74	2,30	2,96	2,00
разница35	1,25	-2,54	-2,49	2,30	1,69	1,56
разница45	-1,73	-1,81	-1,75	0,00	-1,27	-0,44

Квадрат разницы

1,05	1,18	1,00	1,33	0,00	4,94
1,03	0,13	6,70	0,02	0,71	0,20
3,84	1,18	3,43	4,66	4,46	5,98
0,05	8,42	0,01	4,66	0,71	4,00
4,16	0,53	2,52	1,68	0,71	3,16
0,87	0,00	0,72	1,02	4,46	0,05
0,63	3,29	0,81	1,02	0,71	0,05
8,83	0,53	0,54	5,31	8,75	4,00
1,55	6,45	6,19	5,31	2,86	2,42
2,98	3,29	3,07	0,00	1,61	0,20