21

Эта формула также может служить для определения 8. Значение 2_Рез. может быть найдено из (1.13), причем а₀ обьйшо известно с большой точностью.

§ 8. Уравнение распространения волн в пористом материале с твердым скелетом

Предположим пока, что пористый материал обладает твердым скелетом, и рассмотрим движение воздуха в материале.

Так как истинная скорость воздуха в порах изменяется от точки к точке, то мы будем оперировать с объемной скоростью v, определяемой как объем воздуха, проходящего через единицу поверхности, перпендикулярной данному направлению, в единицу

времени. Обозначим пористость мате- риала (отношение объема пор к об- щему объему) через h\ тогда, оче-

dv

видно, при заданном градиенте ^ ,

— будет в

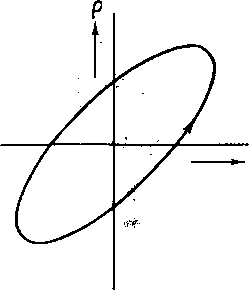
Фиг. 15. Потери при колеба ниях, гистерезис.

Г л. I. Элементарная теория поглощения звука

С первого взгляда кажется странным, что эффект вязкости оказывает влияние на модуль упругости воздуха. Действительно, понятие модуля упругости относится к процессу сжатия и рас­ширения воздуха, когда воздух в целом можно рассматривать неподвижным. Однако важную группу поглощающих материалов составляют акустические пористые штукатурки. Предположим, что в часть пор в материале воздух проникает лишь через срав­нительно узкие каналы. Сдвиг фаз во времени между р и соот­ветствующим изменением плотности р обусловлен сопротивлением этих каналов, так как через них воздух накачивается в поры с трудом. Этот эффект в некоторой степени может иметь место во всех практически применяемых материалах. В штукатурках такие поры могут иметь место внутри «макроскопических» глобул, из которых состоит этот материал. Конечно, сдвиг фаз будет частично обязан также и несовершенству теплового обмена. Выражение (р₀/А) (dp/dД будем обозначать через К. При этом уравнение непрерывности для бегущей волны снова принимает свою обычную форму

Уравнение движения для воздуха, заключенного в материале, будет иметь вид

По сравнению со случаем свободного воздуха сюда входят три новых параметра: структурная постоянная k, пористость h и постоянная сопротивления а¹). Последняя связана с учетом

77 до

вязкости. Для стационарного потока член ^ уничтожается,

тогда а определяется как отношение градиента давления к объ­емной скорости.

Существует несколько причин, обусловливающих повышение кажущейся плотности воздуха, что выражается неравенством k/h > 1. Фактор kjh можно разбить на два: k и 1/А, причем последний описывает обычное влияние пористости. Действительно, если при неизменной структуре пористость h уменьшается, то градиент давления, необходимый для получения той же объемной

Ц В русской акустической терминологии пока не установилось определен­ного названия для величины с. В случае стационарного потока аналогичная величина обычно называется «сопротивлением потоку» или «сопротивлением на продувание». В акустическом случае мы называем о «постоянной сопротивления» или «еоздушным сопротивлением». Последнее представляет буквальный перевод английского термина «air resistance», принятого в большинстве случаев у авторов. (Прим, ред.)

(1.22)

дх~~ h ™ dt

(1.23)